Параметрический синтез (ПС) как одна из основных задач синтеза систем автоматического управления (САУ) используется специалистами по автоматизации при создании САУ и их совершенствовании. В нефтепереработке и нефтехимии [5], энергетике [3] и других отраслях промышленности для стабилизации технологических параметров широко применяются одноконтурные и каскадные САУ. Для специалиста по автоматизации технологических процессов знания методик проведения ПС САУ является важным компонентом его профессиональных компетенций, а их повышение и закрепление является важной задачей на всех этапах его профессионального роста.
Согласно постановлению Правительства РФ от 26 июня 1995 г. № 610 обновление теоретических и практических знаний специалистов является целью повышения квалификации. В условиях непрерывной занятости специалиста на производстве возможна его переподготовка при помощи организации процесса самостоятельного обучения.
Эффективными и широко используемыми средствами организации самостоятельного обучения являются автоматизированные обучающие системы (АОС). При этом процесс анализа выполненных в АОС учебных заданий, как правило, возлагается на человека. Т.к. процесс обучения тесно связан с субъективным мнением обучающего, он сложно поддаётся автоматизации, что усложняет его алгоритмизацию и внедрение в АОС. Однако полноценное самостоятельное обучение возможно организовать с помощью интеллектуализации процесса анализа проведённых учебных заданий как наиболее зависимых от преподавателя. Использование принципов построения интеллектуальных систем при организации АОС позволяет приблизить уровень самообучения к уровню аудиторных занятий.
Предлагается интеллектуализировать определение уровня знаний (УЗ) ПС одноконтурных и каскадных САУ за счёт применения математического аппарата нечёткой логики [4] как наиболее эффективного средства, позволяющего алгоритмизировать рассуждения обучаемого в условиях нечёткости и размытости их определения [7].
Интеллектуализация обучения ПС
В результате анализа частотных методов проведения ПС одноконтурных и каскадных САУ, установлено, что основная часть проведения ПС состоит из построения графиков расширенной амплитудно-фазовой характеристики (РАФХ) и линии Д-разбиения с дальнейшим поиском на них требуемых точек согласно заданным условиям.
Таким образом, для интеллектуализации обучения ПС САУ ТП необходимо обеспечить контроль правильности выбора точек на графиках, необходимых для получения результатов по текущему этапу ПС, на уровне эксперта данной области. Согласно [8] с задачами такого типа успешно справляются экспертные обучающие системы (ЭОС).
Основываясь на работе [4], описание любого определения и понятия, используемого человеком в процессе своей деятельности, можно выполнить с помощью лингвистической переменой. Для интеллектуализации контроля правильности выбора точек на графиках, необходимых для проведения ПС, введена лингвистическая переменная (ЛП) «Расстояние до точки» с соответствующими термами: «За пределом–», «Далеко–», «Близко–», «Совпадает», «Близко+», «Далеко+» и «За пределом+».
Терм «Совпадает» определяет область, в которой, по мнению эксперта, выбранная точка соответствует заданным условиям. Термам «За пределом», «Далеко», «Близко» соответствует расстояние от искомой точки на графике до границы заданного экспертом диапазона. Диапазон на графике выделяется экспертом, исходя из его мнения, что выбор точки на графике за пределом данного диапазона является абсолютно ошибочным и полностью не соответствующим заданным условиям.
Для построения функций принадлежности термов ЛП «Расстояние до точки» используется функция (1), формируемая произведением двух функций вида (2) [6].
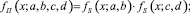 (1)
(1)
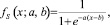 (2)
(2)
где а, b, с, d – некоторые числовые параметры, принимающие произвольные действительные значения и упорядоченные отношением a ≥ b ≥ c ≥ d. Они определяются экспертом в зависимости от типа графика и исходных условий поставленной задачи.
Уровень знаний оценивается с помощью ЛП «Знания» с соответствующими термами «Плохо», «Удовлетворительно», «Хорошо» и «Отлично». Основываясь на [1], для термов ЛП «Знания» построены функции принадлежности по формуле (1) с параметрами, приведёнными в табл. 1.
Таблица 1
Значения функций принадлежности ЛП «Знания»
|
Термы ЛП |
a |
b |
c |
d |
|
Плохо |
–0,7 |
54 |
– |
– |
|
Удовлетворительно |
0,38 |
59 |
–1,2 |
76 |
|
Хорошо |
0,4 |
75 |
–1,6 |
90 |
|
Отлично |
0,58 |
90 |
– |
– |
С помощью ЛП «Знания» можно обозначить уровень знаний на естественном языке в виде обозначенных выше термов. Базовой переменной для ЛП является процент усвоения изучаемого материала и балльно-рейтинговая система оценивания знаний.
Для интеллектуализации изучения ПС, основываясь на алгоритме нечёткого вывода Мамдани [10], составлены правила (нечеткие продукции) нечёткой базы знаний (БЗ), где посылка правил основана на ЛП «Расстояние до точки», а заключением правил является критерий УЗ, основанный на ЛП «Знания». Используемые лингвистические переменные дают возможность эксперту заполнять базу знаний, оперируя понятными ему определениями. Для получения чёткого значения вследствие дефаззификации используется метод центра тяжести [11].
ПС одноконтурных и каскадных САУ
Рассматриваются задачи ПС САУ с пропорционально-интегральным (ПИ), пропорционально-дифференциальным (ПД), пропорционально-интегрально-дифференциальным (ПИД) законами управления на основе расширенных амплитудно-фазовых характеристик (РАФХ) для заданной степени колебательности. В этом случае задача ПС включает два этапа.
1. Определение начальной ωн и конечной ωк частот для построения линии Д-разбиения, удовлетворяющей заданному значению степени колебательности в плоскости настроечных параметров выбранного типа регулятора.
2. Определение рабочей частоты ωраб на линии Д-разбиения и настроечных параметров регулятора, удовлетворяющих наилучшему значению критерия качества переходного процесса.
Сущность первого этапа ПС заключается в том, что выбранный диапазон частот обеспечивает расположение линии Д-разбиения в первом квадранте плоскости настроечных параметров, где на линии Д-разбиения гарантируется устойчивая работа САУ. Здесь, согласно Стефани Е.П. [9], недопустим выбор начальной частоты, соответствующей второму квадранту линии Д-разбиения, и конечной частоты, соответствующей четвертому квадранту линии Д-разбиения. В этих случаях САУ неустойчива.
Для первого этапа ПС одноконтурной САУ по выбору обучаемым ωн и ωк на графике РАФХ (рис. 1) сформированы правила на основании ЛП «Расстояние до точки».
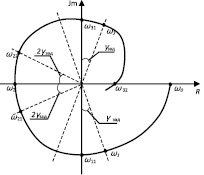
Рис. 1. Расширенная амплитудно-фазовая характеристика объекта управления
Угол γзад на рис. 1 предопределяется требованиями на запас устойчивости САУ. При ПС каждому из рассматриваемых регуляторов для удовлетворения указанных выше условий соответствует свой диапазон частот, определяемый по графику РАФХ. Для ПИ-регулятора этот диапазон от ω1 до ω2, для ПД-регулятора – от ω2 до ω3, для ПИД-регулятора – от ω1 до ω3 (рис. 1). В связи с этим точки с указанными частотами являются искомыми точками. Для определения точности достижения каждой из них применяется ЛП «Расстояние до точки».
В качестве базовой переменной используется процентное соотношение длины рассматриваемого отрезка графика от искомой точки до выставленных экспертами значений границ m1-3 и p1-3 ФП термов ЛП «Расстояние до точки» (рис. 1).
В табл. 2 приводятся выбранные экспертами значения границ ФП термов ЛП «Расстояние до точки» для каждой из этих точек, где m1,2 и p1,2 процентное соотношение отрезка на частотах m3-z и z-p3.
Для второго этапа ПС контроль правильности выбора ωраб и соответствующих ей настроек регулятора также выполняется по ЛП «Расстояние до точки» согласно данным табл. 1. Из работы Е.Г. Дудникова [2] известно соотношения ωраб = 1,2·ωmax (ωmax – частота, соответствующая экстремуму на линии Д-разбиения).
Далее, используя заполненную экспертом БЗ, определяется критерий УЗ по ЛП «Знания».
Таблица 2
Границы термов лингвистической переменной «Расстояние до точки»
|
Искомая точка z |
m3 |
m2 |
m1 |
p1 |
p2 |
p3 |
|
ω1 |
ω0 |
35 |
75 |
30 |
85 |
ω11 |
|
ω2 |
ω21 |
35 |
75 |
25 |
65 |
ω22 |
|
ω3 |
ω31 |
15 |
70 |
25 |
65 |
ω32 |
|
ωраб |
ωн |
20 |
84 |
30 |
80 |
ωк |
|
ωкомп |
0 |
30 |
80 |
20 |
60 |
2 ωраб |
На рис. 2 изображена модель контроля уровня знаний обучаемого при проведении параметрического синтеза одноконтурной САУ.
На рис. 2 показано, что результаты первого этапа параметрического синтеза сводятся в общую базу знаний с данными по второму этапу. На выходе получается итоговый критерий УЗ ПС одноконтурной САУ.
В каскадных САУ сущность ПС состоит в итерационном расчёте настроек стабилизирующего и корректирующего регуляторов. Расчёт заканчивается при достижении заданной величины рассогласования между настроечными параметрами регуляторов на текущем и предыдущем шагах.
В связи с изложенным при контроле изучения ПС каскадной САУ нужно использовать те же методы, что и при изучении ПС одноконтурных САУ. Соответственно для контроля УЗ ПС используются ЛП «Расстояние до точки» и ЛП «Знания» так же, как и при ПС одноконтурной САУ. Так как все этапы ПС одноконтурных САУ здесь проводятся неоднократно, то в качестве выходных параметров используют усреднённый показатель ЛП «Знания» на этапе выбора диапазона частот и на этапе выбора рабочей частоты.
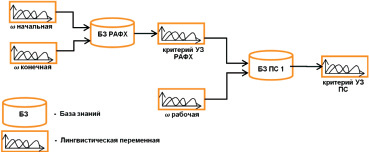
Рис. 2. Модель контроля обучения ПС одноконтурной САУ
Моделирование системы нечёткого вывода
Для создания и моделирования систем нечёткого вывода чаще всего используют специализированные программные продукты MATLAB и FuzzyTECH. Для моделирования системы нечеткого вывода (рис. 1) использовался FuzzyTECH, т.к. он позволяет строить модели из нескольких взаимосвязанных баз знаний, используя более простой и понятный интерфейс, чем интерфейс в MATLAB.
Рассматриваемая нечёткая модель содержит 2 блока правил нечётких продукций для определения уровня знаний первого и второго этапа проведения ПС.
Первый блок правил используется для определения УЗ первого этапа ПС. Он содержит 49 правил нечётких продукций. Второй блок правил используется для определения УЗ второго (заключительного) этапа ПС. Он содержит 28 правил нечётких продукций.
Для анализа рассматриваемой системы нечёткого вывода построена поверхность нечёткого вывода в плоскости начальной и конечной частот, взятых с графика РАФХ.
Поверхность нечёткого вывода на графике (рис. 3, а) позволяет установить зависимость уровня знаний первого этапа ПС от выбора начальной и конечной частоты на графике РАФХ. Поверхность нечёткого вывода на графике (рис. 3, б) позволяет установить зависимость уровня знаний ПС одноконтурной САУ от уровня знаний первого этапа ПС и от выбора частоты настроечных параметров регулятора.
Приведённые нечёткие зависимости полностью соответствуют ожиданиям эксперта, а отсутствие разрывов поверхностей нечёткого вывода свидетельствует об адекватности созданной системы [6]. Таким образом, по созданным правилам нечётких продукций можно определить критерий УЗ данного этапа при любых действиях обучаемого по поиску требуемых точек на графике РАФХ и линии Д-разбиения. Это свидетельствует о возможности применения на практике созданной системы нечёткого вывода для определения уровня знаний обучаемых параметрическому синтезу одноконтурных и каскадных систем автоматического управления.
Выводы
В результате анализа научных работ по интеллектуализации процесса обучения установлено, что контроль уровня знаний обучаемых является важнейшим и неотъемлемым компонентом организации процесса самостоятельного обучения. При этом уровень знаний, как правило, контролируется с помощью систем тестирования. Т.к. уровень знания параметрического синтеза САУ сложно оценить на основе тестирования, необходимо разработать метод интеллектуализации процесса его определения.
На основе проведённого анализа способов интеллектуализации процесса обучения предложено использовать принцип построения экспертных обучающих систем, а также методы, применяемые в нечёткой логике для интеллектуализации обучения ПС САУ ТП.
Используя лингвистические переменные для определения действий обучаемого и уровня получаемых при этом знаний, на основе баз знаний, заполненных экспертом данной области, можно интеллектуализировать процесс самообучения ПС.
Созданная система нечёткого вывода для определения УЗ ПС, смоделирована при помощи программы fuzzyTECH. Результаты моделирования показали, что:
- предложенные правила нечёткой базы знаний обучающей системы адекватно реагируют на все действия обучаемого, необходимые для проведения ПС САУ;
- блок логического вывода экспертной системы корректно обрабатывает подаваемые в него исходные данные;
- полученные на выходе критерии УЗ всех промежуточных и конечных этапов проведения ПС САУ соответствуют ожиданиям экспертов.
а  б
б 
Рис. 3. Зависимость уровня знаний: а – первого этапа ПС от выбора начальной и конечной частоты на графике РАФХ; б – ПС одноконтурной САУ от уровня знаний первого этапа ПС и выбора рабочей частоты регулятора
Это доказывает, что разработанный метод интеллектуализации обучения параметрическому синтезу систем автоматического управления технологическими процессами способен обеспечить самообучение специалистов по автоматизации ТП на достаточно высоком уровне. При этом качество оценивания знаний специалистов будет приближено к мнению экспертов данной области.
Рецензенты:
Игнатюк В.А., д.ф-м.н., профессор Владивостокского государственного университета экономики и сервиса, г. Владивосток;
Дыда А.А., д.т.н., профессор Морского государственного университета им. адм. Г.И. Невельского, г. Владивосток.
Работа поступила в редакцию 17.01.2014.



