В работе [1] рассматривались установившееся течение и теплообмен неньютоновской жидкости в коаксиальном канале бесконечной длины со сформировавшимся профилем скорости и температуры. На практике чаще всего наблюдается изменение профиля температуры по длине, и в связи с этим наибольший интерес представляет исследование влияния основных безразмерных параметров на условия возникновения критических режимов теплообмена в канале с учетом изменения температуры по длине и по радиусу. В данном случае численная реализация поставленных задач усложняется в силу того, что необходимо учитывать конвективный теплоперенос, особенности изменяющегося неньютоновского характера поведения среды, убывание концентраций при условии химической реакции, поэтому в литературе можно встретить небольшое количество работ по данной тематике [5]. Исследование распределений температуры и компонент вектора скорости на начальном участке коаксиального канала в зависимости от интенсивности химического и диссипативного источников при условии преобладания одного из них уже рассмотрены в [3]. Исследования этих характеристик проведены и от некоторых других основных определяющих параметров, таких как параметр Франк-Каменецкого, параметр, характеризующий энергию активации вязкого течения, параметр, характеризующий энергию активации химической реакции, представленных в [3, 2].
Постановка задачи
При построении математической модели стационарного тепломассобмена при течении неньютоновской жидкости в коаксиальном реакторе приняты следующие допущения: течение ламинарное, осесимметричное, стационарное; теплофизические характеристики жидкости, такие как плотность, теплопроводность и теплоемкость меняются в рассматриваемом диапазоне температур незначительно и приняты постоянными; силы тяжести входят в уравнения неявно через избыточное давление; перенос тепла вдоль основного направления движения за счет теплопроводности много меньше вынужденного в этом же направлении; профиль скорости почти мгновенно подстраивается под профиль температуры (Pr >> 1); присутствует химический источник теплоты, распределенный по всему объему канала, заданный реакцией дробного порядка. На границе задаются гидродинамические условия прилипания, тепловые и концентрационные граничные условия первого рода.
При сделанных допущениях и некоторых преобразованиях решаемая система уравнений в цилиндрической системе координат будет выглядеть следующим образом:
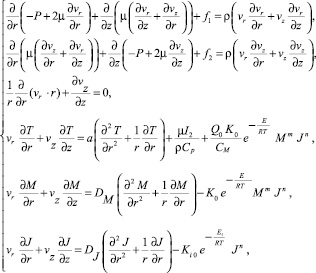 (1)
(1)
где 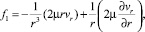
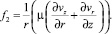
В этих уравнениях r1 ≤ r ≤ r2, 0 ≤ z ≤ L; Q0 – тепловой эффект химической реакции; k0 – константа скорости химической реакции; E – энергия активации химической реакции; a – коэффициент температуропроводности; μ = μ(T, I2, M, J) – динамическая вязкость; ρ – плотность жидкости; R – универсальная газовая постоянная; cp – удельная изобарная теплоемкость; cM – удельная молярная теплоемкость; T – температура; vz, vr – компоненты вектора скорости  ; P – давление; r1, r2 – соответственно внутренний и внешний радиусы коаксиального канала; L – длина канала; Ki0 – константа скорости реакции инициирования; Ei – энергия активации процесса инициирования; ρ – плотность жидкости; R – универсальная газовая постоянная; M – концентрация мономера; J – концентрация инициатора; DM, DJ – коэффициенты взаимной диффузии мономера и инициатора. Второй инвариант тензора скоростей деформации I2 представлен выражением
; P – давление; r1, r2 – соответственно внутренний и внешний радиусы коаксиального канала; L – длина канала; Ki0 – константа скорости реакции инициирования; Ei – энергия активации процесса инициирования; ρ – плотность жидкости; R – универсальная газовая постоянная; M – концентрация мономера; J – концентрация инициатора; DM, DJ – коэффициенты взаимной диффузии мономера и инициатора. Второй инвариант тензора скоростей деформации I2 представлен выражением
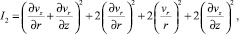 (2)
(2)
Также в системе (1) приняты допущения, что для системы уравнений (1) граничные условия задаются в виде
1. 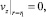
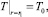
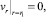
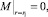
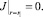
2. 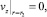
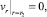
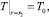
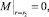
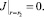 (3)
(3)
3. 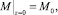
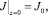
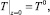
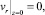
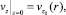
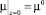 ,
,
где T0 – температура окружающей среды; T0 – температура на входе в коаксиальный канал.
На входе в канал профиль компоненты vz вектора скорости  (то есть функция
(то есть функция 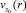 ) является решением задачи
) является решением задачи
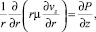 (4)
(4)
при этом 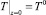 , а составляющая градиента давления
, а составляющая градиента давления 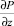 в направлении оси z определяется из выражения
в направлении оси z определяется из выражения
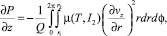 (5)
(5)
где Q – расход жидкости через поперечное сечение канала.
В качестве реологической модели используется модель Кутателадзе–Хабахпашевой [4] для структурно вязкой жидкости, подробно описанная в [3].
Приведя вязкость к безразмерному виду, получим
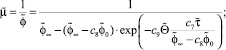 (6)
(6)
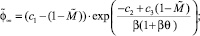
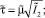 (7)
(7)
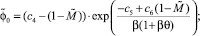
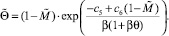 (8)
(8)
Подставляя (6) в (1) и переходя к безразмерным параметрам, имеем
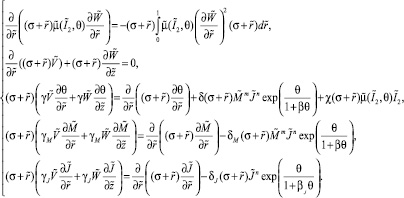 (9)
(9)
Для приведения системы уравнений (1) к безразмерному виду иcпользуются обозначения:
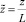 – безразмерная продольная координата;
– безразмерная продольная координата;
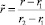 - безразмерная поперечная координата;
- безразмерная поперечная координата;
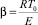 – безразмерный параметр, число Аррениуса;
– безразмерный параметр, число Аррениуса;
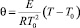 - безразмерная температура;
- безразмерная температура;
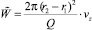 – безразмерная осевая компонента вектора скорости
– безразмерная осевая компонента вектора скорости  ;
;
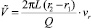 – безразмерная радиальная компонента вектора скорости
– безразмерная радиальная компонента вектора скорости  ;
;
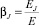 – число Аррениуса из уравнения для инициатора;
– число Аррениуса из уравнения для инициатора;
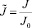 – нормированная по длине концентрация инициатора;
– нормированная по длине концентрация инициатора;
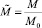 – нормированная по длине концентрация мономера;
– нормированная по длине концентрация мономера;
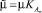 – коэффициент динамической вязкости;
– коэффициент динамической вязкости;
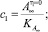
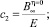
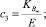
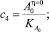
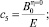
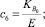
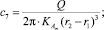
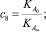
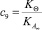 – реологические параметры;
– реологические параметры;
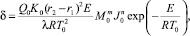 – безразмерный параметр Франк-Каменецкого, характеризующий интенсивность химического источника тепловыделении;
– безразмерный параметр Франк-Каменецкого, характеризующий интенсивность химического источника тепловыделении;
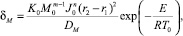
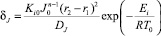 – безразмерный параметр Франк-Каменецкого, характеризующий интенсивность массовыделения в результате химической реакции;
– безразмерный параметр Франк-Каменецкого, характеризующий интенсивность массовыделения в результате химической реакции;
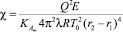 – безразмерный параметр, характеризующий интенсивность тепловыделения от вязкого течения.
– безразмерный параметр, характеризующий интенсивность тепловыделения от вязкого течения.
После перехода к безразмерным параметрам граничные условия первого рода (3) примут вид
1. 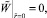
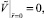
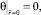
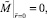
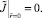
2. 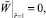
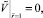
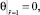
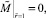
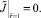 (10)
(10)
3. 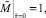
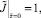
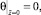
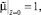
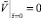
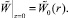
Для решения системы уравнений (9) с граничными условиями (10) используется тот же итерационный алгоритм. Он включает в себя решение соответствующих трехточечных разностных уравнений методом прогонки с пересчетом всех коэффициентов уравнений, зависящих от искомых функций. Вследствие нелинейности системы уравнений (9) и неявного вида функции вязкости были введены дополнительные итерации по вязкости и по нелинейному свободному члену.
Результаты
На основании проведенного комплекса численных исследований было выявлено, что критическое значение конкретного управляющего параметра изменяется при изменении других управляющих параметров. Таким образом, для критического параметра δ было решено построить его зависимости от реологических параметров. Данные зависимости задаются поверхностями, которые называют критическими поверхностями. Они дают более общее наглядное представление о взаимном влиянии безразмерных параметров друг на друга, а также об их влиянии на возникновение критических режимов теплообмена в реакторе.
Критические поверхности разделяют область допустимых значений безразмерных управляющих параметров на две подобласти, одна из них соответствует безопасному режиму теплообмена в реакторе, а другая ‒ критическому режиму теплообмена. В случае, когда безразмерные параметры принимают значения из области безопасного режима теплообмена, критические явления в реакторе не возникают. Ещё один положительный момент критических поверхностей состоит в том, что объединяют в себе множество зависимостей, определяющих процесс параметров от управляющих параметров. В данной работе критические поверхности строятся для критических значений управляющих параметров в точках с координатой 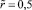 и координатой
и координатой  , которая меняется в пределах конечной допустимой длины коаксиального реактора.
, которая меняется в пределах конечной допустимой длины коаксиального реактора.
В используемой в данной работе реологической модели параметр c9 находится под экспонентой в зависимости вязкости от скорости сдвига и температуры, а параметр c8 – перед экспонентой данной зависимости. В данном случае нельзя провести классификацию типов жидкостей, соответствующих определенным значениям параметров c1, c2, c3, c4, c5, c6, c7, c8, c9, как это было сделано относительно параметров c0 и c1 в бесконечном коаксиальном канале в [1], но определенную приближенную аналогию провести можно.
Параметру c0 в реологической модели в [1] соответствует параметр c8 из реологической модели в [1], параметру c1 ‒ параметр c9, а параметру α параметр c5. При c8 > 1, c9 > 0 жидкость считается псевдопластичной, при c8 < 1, c9 > 0 дилатантной и при c8 = 1, c9 > 0 ньютоновской. Поэтому на рисунке приведены критические поверхности, содержащие именно эти параметры, а именно соответствующие зависимости параметра δ от реологических параметров c8 и c5χ, и от параметров c9 и c5χ.
а 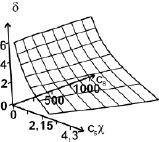 б
б 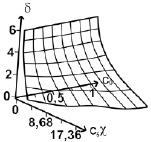
Критические поверхности зависимостей δ = δ(c8, c5χ) и δ = δ(c9, c5χ)
Как видно на графиках, при увеличении тепловыделений от диссипации (c5χ растет) при движении реакционной смеси в реакторе критические значения параметра δ уменьшаются. Таким образом, при превалировании величины энергии активации вязкого течения над энергией активации химической реакции диапазон критических значений определяющих процесс, соответствующий безопасному режиму работы, становится уже. Отметим, что при уменьшении значений c8 и фиксированных значениях c5χ существуют области на поверхности (рисунок, а), где происходит существенное изменение δ при небольшом изменении c8.
Как следует из графика δ = δ(c9, c5χ) на рисунке (б), критические значения параметра δ не изменяются при изменении параметра c9.
Рецензенты:
Вачагина Е.К., д.т.н., зав. лабораторией ТФИ, Исследовательский центр проблем энергетики, ФБУН «Казанский научный центр Российской академии наук», г. Казань;
Молочников В.М., д.т.н., зав. лабораторией ГИТ, Исследовательский центр проблем энергетики, ФБУН «Казанский научный центр Российской академии наук», г. Казань
Работа поступила в редакцию 17.01.2014.



