Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Прогнозирование развития ситуаций представляет интерес в самых различных сферах деятельности человека. Для решения этой задачи известно большое число подходов и методов. Важное место среди них занимает логическое прогнозирование. К методам логического прогнозирования обычно относят создание прогнозного сценария, морфологический анализ, метод исторических аналогий, прогнозирование по образцу (эталону) и др [1]. Перспективным подходом при построении методов логического прогнозирования является использование моделирования рассуждений, в частности, логического вывода заключений [2]. В этом случае ситуация описывается средствами формальной системы (исчисления высказываний или исчисления предикатов), а ее развитие прогнозируется с помощью дедуктивного логического вывода [3, 5]. Дедуктивный вывод, при проведении которого новые утверждения выступают следствиями из уже имеющихся утверждений, хотя и имеет ограниченную область применения, но надежен при условии истинности посылок. В простейшем случае дедуктивный вывод состоит в установлении факта логического следования из посылок заданного заключения [4].

Постановка задачи

Задачу логического вывода следствий с построением схемы вывода можно сформулировать следующим образом. Имеются исходные непротиворечивые посылки, заданные в виде множества дизъюнктов M^ = {D1, D2, …, DI}. При этом каждый дизъюнкт содержит один литерал без инверсии. Множество M^ включает подмножество однолитеральных дизъюнктов MF – фактов. Также имеется множество новых фактов mF = {L1, L2,…, Lp,…, LP}. Схема вывода описывается множеством литералов с параметрами: S = {L(j, k); L ∈ A, j, k ∈ N}, где L – литерал из множества A различных литералов, используемых в посылках; N – номер посылки (дизъюнкта); j – номер посылки, из вершины которой на схеме выходит, а k – номер посылки, в вершину которой входит дуга, помеченная литералом L. Параметр j называется левым, а k – правым номером литерала L.

Тогда задачу вывода логических следствий (литералов без инверсий) можно сформулировать так:

1) определить множество следствий MS и семейство множеств следствий S = {s0, s1, …, sh, …, sH}, в котором множество следствий sh содержит следствия, выводимые с помощью множества посылок Mh (Mh ⊆ M^) из множества следствий sh-1: sh-1, Mh ⇒ sh и s0 = MF ∩ mF;

2) сформировать описание O схемы логического вывода, по которому может быть построена схема вывода следствий, в виде семейства множеств O = {g1, g2, …, gh, …, gH}, где gh – множество литералов, полученных при формировании описания схемы на h-м шаге вывода;

3) определить подмножество конечных следствий s+ ⊆ MS, из которых не могут быть выведены новые следствия.

Для осуществления логического вывода с формированием описания схемы используется специальная процедура – процедура логического вывода следствий, основанная на операции обобщенного деления дизъюнктов [3].

Метод вывода следствий основан на вышеуказанной процедуре и состоит из ряда шагов, на каждом из которых выполняется процедура вывода V″. Причем результаты выполнения процедуры i-го шага становятся исходными данными для процедуры i + 1-го шага. Процесс заканчивается в случае, если дальнейший вывод следствий невозможен (получено значение признака p = 1).

Обозначим через h номер шага вывода, а через P – общий признак продолжения вывода (P = 0 – продолжение вывода возможно, P = 1 – продолжение вывода не возможно). Тогда описание метода может быть представлено в следующем виде.

1. Определение начальных значений: h = 1, M^ ≠ ∅, mF ≠ ∅, M1 = M^–MF (исключение из исходного множества дизъюнктов однолитеральных дизъюнктов – фактов). Формируется выводимый дизъюнкт R1, состоящий из литералов множества mF, и вспомогательный дизъюнкт r, состоящий из литералов фактов исходных посылок MF. Определяется множество следствий s0, совпадающих с фактами MF, имеющимися в исходных посылках: s0 = MF ∩ mF, S0 = {s0}. Устанавливается начальное значение общего признака продолжения вывода P0 = 0 и семейства множеств частных, описывающих схему вывода следствий G0 = ∅.

2. Выполнение h-й процедуры вывода.

V″h = <Mh, Rh, ph, Mh + 1, Rh + 1, sh> .

3. Формирование семейств множеств следствий и множеств частных и проверка признаков. Формируется семейство множеств следствий Sh = Sh – 1 ∪ {sh} и семейство множеств частных Gh = Gh – 1 ∪ {gh}. Вычисляется значение общего признака продолжения вывода Ph = Ph – 1∨ph. Если Ph = 0, то вывод продолжается: h увеличивается на единицу и производится переход к п. 2, иначе вывод завершается.

Полученные следствия содержатся в семействе множеств S = Sh, а общее множество следствий образуется путем объединения множеств семейства Sh: MS = s0 ∪ s1 ∪ s2 ∪ … ∪ sh.

Описание схемы вывода следствий представляет собой семейство множеств частных O = Gh. Это множество состоит из множеств частных, содержащих литералы с параметрами. Литералом помечается дуга схемы, причем первый параметр литерала представляет собой вершину схемы, из которой выходит, а второй – вершину, в которую входит дуга. Таким образом, множество литералов Gh однозначно определяет схему логического вывода. Построение схемы осуществляется в соответствии с шагами логического вывода: в начале на схему наносятся вершины и дуги, описываемые во множестве литералов G1, затем к ним добавляются связи и вершины, описываемые во множестве литералов G2, и т.д.

Множество конечных следствий определяется следующим образом:

s + = ,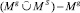

где Mg = g1 ∪ g2 ∪ … ∪ gh, а особенностью операции специального объединения множеств литералов является поглощение литерала L(j, +) ∈ MS литералом L(j, k) ∈ Mg.

Применение метода логического вывода

Применение метода вывода следствий рассмотрим на следующем примере. Пусть исходные посылки заданы множеством секвенций:

1) AB → C;

2) 1 → D;

3) CD → E;

4) EV → L;

5) 1 → P;

6) L → R;

7) MP → N;

8) 1 → S;

9) R → U;

10) N→ V;

11) SR → X;

12) X → Z.

Необходимо определить, какие следствия можно вывести из фактов mF = {A, B, M}.

Представим посылки в виде дизъюнктов:

D1 = A(+ ,1)∨B(+ ,1)∨C(1, +);

D2 = D(2, +);

D3 = C(+ ,3)∨D(+ ,3)∨E(3, +);

D4 = E(+ ,4)∨V(+ ,4)∨L(4, +);

D5 = P(5, +);

D6 = L(+ ,6)∨R(6, +);

D7 = M(+ ,7)∨P(+ ,7)∨N(7, +);

D8 = S(8, +);

D9 = R(+ ,9)∨U(9, +);

D10 = N(+ ,10)∨V(10, +);

D11 = S(+ ,11)∨R(+ ,11)∨X(11, +);

D12 = X(+ ,12)∨Z(12, +).

Представим в виде дизъюнктов факты, из которых требуется определить следствия:

D13 = A(13, +); D14 = B(14, +);

D15 = M(15, +).

Определение начальных значений: h = 1, M^ = {D1, D2, D3, D4, D5, D7, D8, D9, D10, D11, D12}, mF = {D13, D14, D15}, M1 = M^–MF = {D1, D3, D4, D7, D9, D10, D11, D12}. Формирование выводимого дизъюнкта R1 = A(13, +)∨B(14, +)∨M(15, +), состоящего из литералов множества mF, и вспомогательного дизъюнкта r = D(2, +)∨P(5, +)∨S(8, +), составленного из литералов фактов исходных посылок MF. Определение множества следствий s0, совпадающих с фактами MF, имеющимися в исходных посылках: s0 = MF ∩ mF = ∅, S0 = {s0} = ∅. Формирование начального значения общего признака решений Q0 = 1, так как s0 = ∅. Установка начального значения общего признака продолжения вывода P0 = 0 и семейства множеств частных, описывающих схему вывода следствий G0 = ∅.

Шаг 1.

Выполнение процедуры вывода V″1 = <M1, R1, p1, M2, R2, s1, g1> .

1. Производится обобщенное деление дизъюнктов исходных посылок на дизъюнкт R1: Di %R1 = < ai, bi > , i = 1, ..., 12. При этом b1 = C(1, +), b7 = P(+ ,7)∨N(7, +), остальные остатки равны единице. Образуется начальное множество частных: g1* = a1∪a7, где a1 = {A(13,1),B(14,1)}, a7 = {M(15,7)}. Анализируются остатки bi, i = 1, ..., 12. Так как есть остатки, отличные от единицы, то выполняется следующий пункт.

2. Проверяется наличие фактов. Полученные ранее остатки делятся на вспомогательный дизъюнкт r: b1 %r = <a′1, b′1> , b7 %r = <a′7, b′7> . В результате получается: a′1 = ∅, b′1 = 1, B1 = b′1 и a′7 = {P(5,7)}, b′7 = N(7, +), B7 = b′. Корректируется множество частных: g1 = g1*∪a′1∪a′7 = {A(13,1), B(14,1), M(15,7), P(5,7)}, и выполняется следующий пункт.

3. Формируется множество следствий s1. В это множество включаются литералы остатков B1 и B7: s1 = {C(1, +), N(7, +)}.

4. Формируется новое множество исходных секвенций

M2 = M1 ‒ M0 = {D3, D4, D6, D9, D10, D11, D12},

где M0 = {D1, D7} – подмножество дизъюнктов множества M1, для которых были получены остатки, представляющие собой литерал без инверсии.

5. Формируется новый выводимый дизъюнкт R2 = C(1, +)∨N(7, +) как дизъюнкция литералов множества следствий s1.

6. Устанавливается значение признака p1. Поскольку получено непустое множество s1, то p1 = 0 (возможно продолжение вывода).

Формирование семейств множеств следствий и множеств частных и проверка признаков. Формируется семейство множеств следствий

S1 = S0∪{s1} = {{C(1, +),N(7, +)}}

и семейство множеств частных G1 = G0 ∪ {g1} = {{A(13, 1), B(14, 1), M(15, 7), P(5, 7)}}. Вычисляется значение общего признака продолжения вывода P1 = P0∨p1 = 0. Поскольку P1 = 0, то вывод продолжается: h увеличивается на единицу и производится переход к следующему шагу.

Шаг 2.

Выполнение процедуры вывода V″2 = <M2, R2, p2, M3, R3, s2, g2> .

1. Производится обобщенное деление дизъюнктов посылок множества M2 на дизъюнкт R2. При этом a3 = {C(1,3)}, b3 = D(+ ,3)∨E(3, +), a10 = {N(7,10)}, b10 = V(10, +), остальные остатки равны единице. Образуется начальное множество частных: g2* = a3 ∪ a10 = {C(1, 3), N(7, 10)}. Так как есть остатки, отличные от единицы, то выполняется следующий пункт.

2. Проверяется наличие фактов. Полученные ранее остатки делятся на вспомогательный дизъюнкт r: b3 %r = <a′3, b′3> , b10 %r = <a′10, b′10> . В результате получается: a′3 = {D(2, 3)}, b′3 = E(3, +), B3 = b′3 и a′10 = ∅, b′10 = 1; B10 = b10. Корректируется множество частных: g2 = g2* ∪ a′3 ∪ a′10 = {C(1, 3), N(7, 10), D(2, 3)}, и выполняется следующий пункт.

3. Формируется множество следствий s2. В это множество включаются литералы остатков B3 и B10: s2 = {E(3, +),V(10, +)}.

4. Формируется новое множество исходных секвенций M3 = M2 – M0 = {D4, D6, D9, D11, D12}, где M0 = {D3, D10} – подмножество дизъюнктов множества M2, для которых были получены остатки, представляющие собой литерал без инверсии.

5. Формируется новый выводимый дизъюнкт R3 = E(3, +)∨V(10, +) как дизъюнкция литералов множества следствий s2.

6. Устанавливается значение признака p2. Поскольку получено непустое множество s2, то p2 = 0 (возможно продолжение вывода).

Формирование семейств множеств следствий и множеств частных и проверка признаков. Формируется семейство множеств следствий: S2 = S1 ∪ {s2} = {s1, s2} и семейство множеств частных: G2 = G1 ∪ {g2} = {g1, g2} = {{A(13, 1), B(14, 1), M(15, 7), P(5, 7)}, {C(1, 3), N(7, 10), D(2, 3)}}. Вычисляется значение общего признака продолжения вывода P2 = P1∨p2 = 0. Поскольку P2 = 0, то вывод продолжается: h увеличивается на единицу и производится переход к следующему шагу.

Шаг 3.

Выполнение процедуры вывода V″3 = <M3, R3, p3, M4, R4, s3, g3> .

1. Производится обобщенное деление дизъюнктов посылок множества M3 на дизъюнкт R3. При этом a4 = {E(3, 4), V(10, 4)}, b4 = L(4, +), остальные остатки равны единице. Образуется начальное множество частных: g3* = a4. Так как есть остатки, отличные от единицы, то выполняется следующий пункт.

2. Проверяется наличие фактов. Полученный ранее остаток делится на вспомогательный дизъюнкт r: b4 %r = < a′4, b′4 > . В результате получается: a′4 = ∅, b′4 = 1; B4 = b4. Принимается g3 = g3* = {E(3, 4), V(10, 4)} и выполняется следующий пункт.

3. Формируется множество следствий s3. В это множество включаются литерал остатка B4: s3 = {L(4, +)}.

4. Формируется новое множество исходных секвенций M4 = M3 – M0 = {D6, D9, D11, D12}, где M0 = {D4} – подмножество дизъюнктов множества M3, для которых были получены остатки, представляющие собой литерал без инверсии.

5. Формируется новый выводимый дизъюнкт R4 = L(4, +) как дизъюнкция литералов множества следствий s3.

6. Устанавливается значение признака p3. Поскольку получено непустое множество s3, то p3 = 0 (возможно продолжение вывода).

Формирование семейств множеств следствий и множеств частных и проверка признаков. Формируется семейство множеств следствий: S3 = S2 ∪ {s3} = {s1, s2, s3} и семейство множеств частных: G3 = G2 ∪ {g3} = {g1, g2, g3}. Вычисляется значение общего признака продолжения вывода P3 = P2∨p3 = 0. Поскольку P3 = 0, то вывод продолжается: h увеличивается на единицу и производится переход к следующему шагу.

Шаг 4.

Выполнение процедуры вывода V″4 = <M4, R4, p4, M5, R5, s4, g4> .

1. Производится обобщенное деление дизъюнктов посылок множества M4 на дизъюнкт R4. При этом a6 = {L(4,6)}, b6 = R(6, +), остальные остатки равны единице. Образуется начальное множество частных: g4* = a6. Так как есть остатки, отличные от единицы, то выполняется следующий пункт.

2. Проверяется наличие фактов. Полученный ранее остаток делится на вспомогательный дизъюнкт r: b6 %r = < a′6, b′6 > . В результате получается: a′6 = ∅, b′6 = 1; B6 = b6. Принимается g4 = g4* = {L(4, 6)} и выполняется следующий пункт.

3. Формируется множество следствий s4. В это множество включаются литерал остатка B6: s4 = {R(6, +)}.

4) Формируется новое множество исходных секвенций M5 = M4 – M0 = {D9, D11, D12}, где M0 = {D6} – подмножество дизъюнктов множества M4, для которых были получены остатки, представляющие собой литерал без инверсии.

5. Формируется новый выводимый дизъюнкт R5 = R(6, +), как дизъюнкция литералов множества следствий s4.

6. Устанавливается значение признака p4. Поскольку получено непустое множество s4, то p4 = 0 (возможно продолжение вывода).

Формирование семейств множеств следствий и множеств частных и проверка признаков. Формируется семейство множеств следствий: S4 = S3 ∪ {s4} = {s1, s2, s3, s4} и семейство множеств частных: G4 = G3 ∪ {g4} = {g1, g2, g3, g4}. Вычисляется значение общего признака продолжения вывода P4 = P3∨p4 = 0. Поскольку P4 = 0, то вывод продолжается: h увеличивается на единицу и производится переход к следующему шагу.

Шаг 5.

Выполнение процедуры вывода V″5 = <M5, R5, p5, M6, R6, s5, g5> .

1. Производится обобщенное деление дизъюнктов посылок множества M5 на дизъюнкт R5. При этом a9 = {R(6, 9)}, b9 = U(9, +), a11 = {R(6, 11)}, b11 = S(+ ,11)∨X(11, +), остальные остатки равны единице. Образуется начальное множество частных: g5* = a9 ∪ a11. Так как есть остатки, отличные от единицы, то выполняется следующий пункт.

2. Проверяется наличие фактов. Полученные ранее остатки делятся на вспомогательный дизъюнкт r: b9 %r = < a′9, b′9 >, b11 %r = < a′11, b′11 >. В результате получается: a′9 = ∅, b′9 = 1, B9 = b9; a′11 = {S(8, 11)}, b′11 = X(11, +), B11 = b′11. Принимается g5 = g5* ∪ a′9∪a′11 = = {R(6, 9), R(6, 11), S(8, 11)} и выполняется следующий пункт.

3. Формируется множество следствий s5. В это множество включаются литералы остатков B9, B11: s5 = {U(9, +),X(11, +)}.

4. Формируется новое множество исходных секвенций M6 = M5 – M0 = {D12}, где M0 = {D9, D11} – подмножество дизъюнктов множества M5, для которых были получены остатки, представляющие собой литерал без инверсии.

5. Формируется новый выводимый дизъюнкт R6 = U(9, +)∨X(11, +), как дизъюнкция литералов множества следствий s5.

6. Устанавливается значение признака p5. Поскольку получено непустое множество s5, то p5 = 0 (возможно продолжение вывода).

Формирование семейств множеств следствий и множеств частных и проверка признаков. Формируется семейство множеств следствий: S5 = S4 ∪ {s5} = {s1, s2, s3, s4, s5} и семейство множеств частных: G5 = G4∪{g5} = {g1, g2, g3, g4, g5}. Вычисляется значение общего признака продолжения вывода P5 = P4∨p5 = 0. Поскольку P5 = 0, то вывод продолжается: h увеличивается на единицу и производится переход к следующему шагу.

Шаг 6.

Выполнение процедуры вывода V″6 = <M6, R6, p6, M7, R7, s6, g6> .

1. Производится обобщенное деление дизъюнктов посылок множества M6 на дизъюнкт R6. При этом a12 = {X(11, 12)}, b12 = Z(12, +), остальные остатки равны единице. Образуется начальное множество частных: g6* = a12. Так как есть остатки, отличные от единицы, то выполняется следующий пункт.

2. Проверяется наличие фактов. Полученный ранее остаток делится на вспомогательный дизъюнкт r: b12 %r = < a′12, b′12 >. В результате получается: a′12 = ∅, b′12 = 1; B12 = b12. Принимается g6 = g6* = {X(11, 12)} и выполняется следующий пункт.

3. Формируется множество следствий s6. В это множество включаются литерал остатка B121: s6 = {Z(12, +)}.

4) Формируется новое множество исходных секвенций M7 = M6 – M0 = ∅, где M0 = {D12} – подмножество дизъюнктов множества M6, для которых были получены остатки, представляющие собой литерал без инверсии. Поскольку из множества M6 исключаются все дизъюнкты: M7 = ∅, то принимается q6 = 1, p6 = 1 – дальнейший вывод невозможен.

Формирование семейств множеств следствий и множеств частных и проверка признаков. Формируется семейство множеств следствий: S6 = S5 ∪ {s6} = {s1, s2, s3, s4, s5, s6} и семейство множеств частных: G6 = G5∪{g6} = {g1, g2, g3, g4, g5, g6}. Вычисляется значение общего признака продолжения вывода P6 = P5∨p6 = 1. Поскольку P6 = 1, то вывод завершается.

Полученные следствия содержатся в семействе множеств S = S6, а общее множество следствий образуется путем объединения множеств семейства S6: MS = {C(1, +), N(7, +), E(3, +), V(10, +), L(4, +), R(6, +),U(9, +), X(11, +), Z(12, +)}.

Описание схемы вывода следствий представляет собой семейство множеств частных O = G6. содержащих литералы с параметрами. Построение схемы осуществляется в соответствии с шагами логического вывода: в начале на схему наносятся вершины и дуги, описываемые во множестве литералов G1, затем к ним добавляются связи и вершины, описываемые во множестве литералов G2, и т.д. (см. рисунок).

Множество конечных следствий определяется на основе множеств MS и Mg = g1 ∪ … ∪ g6 = {A(13, 1), B(14, 1), M(15, 7), P(5, 7), C(1, 3), D(2, 3), N(7, 10), E(3, 4), V(10, 4), L(4, 6), R(6, 9), R(6, 11), S(8, 11), X(11, 12)} следующим образом: s + = 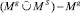= {U(9, +), Z(12, +)}.

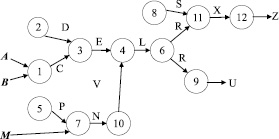
Схема вывода следствий (обозначения фактов множества MF выделены курсивом)

Таким образом, результатом вывода является следующее семейство множеств следствий: S6 = {{C, N}, {E, V}, {L}, {R}, {U, X}, {Z}}. В процессе вывода получено 9 различных следствий: MS = {C, N, E, V, L, R, U, X, Z}. Следствия U и Z являются конечными, так как дальнейший вывод из них невозможен.

Процесс логического вывода в данном примере требует шесть шагов. Формируемые на каждом шаге выводимые дизъюнкты Rh и соответствующие им множества следствий sh (h = 1, 2, 3, 4, 5, 6, 7) приведены в таблице.

Выводимые дизъюнкты и множества следствий, формируемые в процессе логического вывода

Заключение

Предложенный метод логического вывода позволяет находить следствия из заданных фактов для знаний, представленных формулами исчисления высказываний, и строить схему вывода логических следствий.

Метод обладает глубоким параллелизмом, что позволяет эффективно применять его для многопараметрического долгосрочного прогнозирования при реализации интеллектуальных систем на современных высокопроизводительных параллельных вычислительных платформах.

Рецензенты:

Пономарев В.И., д.т.н., профессор, директор закрытого акционерного общества «НПП «Знак», г. Киров;

Частиков А.В., д.т.н., профессор, декан факультета Прикладной математики и телекоммуникаций, ФГБОУ ВПО ВятГУ, г. Киров.

Работа поступила в редакцию 15.01.2014.