Целью настоящей работы является выработка единой концепции к описанию поверхностных явлений на основе теории Ван-дер-Ваальса на примере межфазного слоя жидкость-газ.
Классическая теория поверхностных явлений до настоящего времени базируется на теоретическом уравнении, разработанном практически одновременно Юнгом и Лапласом в начале девятнадцатого века. Требования сегодняшнего дня вызывают необходимость доработки, уточнения и дальнейшего развития этой теории. Так, в работе [3] отмечается, что за время существования классического уравнения не получено достаточно полного его экспериментального подтверждения. Указаны публикации, в которых справедливость этого уравнения ставится под сомнение. В той же работе на основании тщательного анализа литературных источников делается вывод о том, что напряжений, действующих вдоль свободной поверхности жидкости, в опытах не обнаружено. В связи с этим поверхностное натяжение как реально действующая сила в равновесных жидких структурах или отсутствует, или настолько мало, что им можно пренебречь по сравнению с силами объемного взаимодействия. Предлагается коэффициент поверхностного натяжения заменить коэффициентом объемного натяжения, пределом прочности (текучести) межфазной контактной границы или предельным напряжением адгезии.
Сказанное свидетельствует о том, что в настоящее время не существует единой концепции к описанию поверхностных явлений. В данной работе сделана попытка выработки такой концепции. В ее основу положена теория неидеальных газов Ван-дер-Ваальса. Выбор этой теории не является случайным, а обусловлен следующими причинами. Прежде всего, теория Ван-дер-Ваальса позволяет описывать состояние среды как в жидком, так и парообразном состоянии. В связи с тем, что межфазный слой жидкость-газ занимает промежуточное положение между этими состояниями, можно предположить, что поверхностные явления также могут быть описаны посредством теории Ван-дер-Ваальса. Традиционно считается, что промежуточная область между жидкой и паровой фазами на изотерме Ван-дер-Ваальса является областью неустойчивых состояний вещества. Отмечается, что некоторые из этих состояний могут быть реализованы в определенных специфических условиях [2]. Так как закономерности строения межфазных слоев до настоящего времени не изучены, можно предположить, что состояния вещества, неустойчивые в объемных фазах, могут оказаться вполне устойчивыми в тонких разделительных межфазных слоях.
Уравнение Ван-дер-Ваальса, составляющее основу теории, записывается в виде
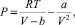 (1)
(1)
где P – внешнее давление; V– молярный объем; Т – абсолютная температура; R– универсальная газовая постоянная. Первое слагаемое в правой части уравнения определяет давление сил отталкивания, действующих в среде, второе – давление сил притяжения. Графическое представление зависимости (1) при фиксированной температуре носит название изотермы Ван-дер-Ваальса. Общий вид изотермы представлен на рис. 1 в верхней части рисунка, а в нижней части показаны зависимости давлений притяжения и отталкивания от удельного объема среды. Удельные объемы среды измеряются в м3/моль, а значения давлений – в паскалях (Па = н/м3).
Состояния жидкой среды, отвечающие различным участкам изотермы, достаточно подробно изложены в работе [2]. В соответствии с традиционными представлениями [7] ветвь изотермы со значениями удельных давлений V < V2 описывает жидкое состояние среды, а при V > V4 – газообразное. Участок изотермы при V4 > V > V2 выбрасывается из рассмотрения в связи с противоречивой зависимостью давления от объема. На толщине межфазного слоя жидкость-газ плотность среды, а значит, и значение удельного объема изменяется на три порядка, в связи с чем необходимо рассмотреть механизм такого перехода. Одним из возможных способов его реализации является использование представлений Я.И. Френкеля о дырочном строении жидкостей [8].
В соответствии с теорией Я.И. Френкеля объем жидкости не является однородным, а содержит отдельные межмолекулярные полости (дырки), заполненные паром. Возникновение таких образований носит характер флуктуаций, возникающих за счет движения молекул. В соответствии с этим газовые полости могут образовываться, исчезать и появляться вновь в другой части объема. Использование такого подхода для описания межфазного слоя жидкость-газ позволяет рассматривать среду с определенным значением удельного объема как дисперсию паровых пузырьков в жидкости или дисперсию капель жидкости в насыщенном паре. Изменение содержания жидкой и паровой фаз в межфазном слое позволяет формировать среду со значениями удельных объемов от собственно жидкости (объемной фазы) до среды с удельным объемом насыщенного пара. При этом каждому значению удельного объема среды в указанных пределах можно поставить в соответствие определенную точку на изотерме Ван-дер-Ваальса. Следует также отметить, что система жидкость-газ может принимать только те физические состояния, которым отвечает определенная точка изотермы.
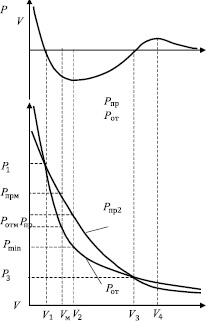
Рис. 1. Изотерма Ван-дер-Ваальса
Представление среды дисперсной системой связано с проявлением некоторых особенностей в описании силовых межфазных взаимодействий. В монографии Р.И. Нигматулина [5] указывается на возникновение объемной межфазной силы, связанной с действием сил давления. Величина этой силы определяется как
R21 = P1∇α1. (2)
Здесь индексом 1 помечены величины, относящиеся к непрерывной дисперсионной фазе, индексом 2 – к дисперсной; R21 – объемная сила, действующая со стороны дисперсных частиц на дисперсионную фазу; P1 – давление в дисперсионной среде; ∇α1 – градиент объемной концентрации дисперсионной фазы.
Изотерма Ван-дер-Ваальса, изображенная на рис. 1, создает общие представления о характере ее поведения. Графическое построение кривой в реальном масштабе проблематично, т.к. значения удельных объемов по оси абсцисс меняются на несколько порядков. В связи с этим результаты вычислений приведены в табличной форме. В таблице представлены расчетные значения давлений в четырех характерных точках изотермы для воды при температуре 20 °С. Значения параметров уравнения Ван-дер-Ваальса взяты из справочника.
Расчетные значения давлений в ключевых точках изотермы Ван-дер-Ваальса для воды при температуре 20 °С
|
V |
V1 3,63∙10–5 |
V2 4,44∙10–5 |
V3 1,87∙10–4 |
V4 3,78∙10–4 |
|
Pот |
4,14∙108 |
1,74∙108 |
1,55∙107 |
7,01∙106 |
|
Pпр |
4,14∙108 |
2,77∙108 |
1,55∙107 |
3,81∙106 |
|
P |
0 |
–1,03∙108 |
0 |
3,20∙106 |
С учетом приведенных в таблице значений давлений и малой толщины межфазного слоя межфазная объемная сила, определяемая уравнением (2), может оказать решающее воздействие на формирование межфазного силового поля.
Рассмотрим межфазный слой жидкость-газ и определим участок изотермы, отвечающий ему. Очевидно, что точка межфазного слоя, лежащая на границе с объемной (невозмущенной) жидкостью, отразится на изотерме точкой с координатами: V = V1; Р = 0. В этой точке выполняются условия механического равновесия среды, т.е. равенство давлений притяжения и отталкивания. Переход к точкам межфазного слоя означает увеличение значений удельного объема, т.е. переход в область значений V > V1. Этот переход сопровождается одновременным уменьшением как внешнего давления Р, так и давлений притяжения Pпр и отталкивания Pот (см. рис. 1). По существующим представлениям эта область является областью неустойчивых состояний среды. Допустим возможность устойчивого равновесия среды в этой области изотермы в условиях межфазного слоя.
Прежде всего, необходимо определить вторую границу межфазного слоя, т.е. область контакта жидкой и газовой фаз. Этой области должна соответствовать определенная точка изотермы Ван-дер-Ваальса и эта точка должна лежать на ветви изотермы, описывающей жидкое состояние среды. Кроме того, эта точка как граничная точка межфазного слоя должна обладать особенностью, отличающей ее от близлежащих точек изотермы. Очевидно, что такой точкой является точка изотермы с координатами V = V2; P = Pmin. С учетом особого положения точки в ней должна происходить перестройка структуры среды. В соответствии с представлениями Я.И. Френкеля, среда на нисходящей ветви изотермы может рассматриваться как дисперсная система, состоящая из жидкой дисперсионной фазы с включениями паровых пузырьков. С уменьшением значения удельного объема возможна инверсия фаз, при которой система будет представлять дисперсию капель жидкости в газовой дисперсионной среде. Определив возможные границы межфазного слоя, можно перейти к рассмотрению межфазных силовых взаимодействий.
Обратим внимание на отсутствие внешних силовых факторов в межфазном слое, которые могли бы изменить внешнее давление Р. В соответствии с этим любые изменения давления в межфазном слое могут быть обусловлены только внутренними для среды силовыми факторами. В работе [2] отмечается, что наличие твердой поверхности в межфазном слое жидкость – твердое может рассматриваться как внешнее воздействие на жидкую фазу, экранирующее силы межмолекулярного притяжения в ней. По аналогии существование межфазного слоя жидкость – газ предполагает наличие свободной поверхности жидкости. Формально для ее образования необходимо совершить внешнее воздействие (затратить энергию), связанное с разделением объемной фазы жидкости для образования свободной поверхности. Таким образом, присутствие газовой фазы может рассматриваться как реализованное внешнее воздействие, направленное на снижение давления в среде.
Для определения реакции системы на это воздействие воспользуемся принципом ЛеШателье: если на систему, находящуюся в устойчивом равновесии, воздействовать извне, изменяя какое-либо из условий равновесия, то в системе усиливаются процессы, направленные на компенсацию внешнего воздействия. Таким образом, наличие межфазного слоя предполагает возникновение реакции системы, направленной на повышение давления в системе. Оценим возможность возникновения такой реакции.
Теория Ван-дер-Ваальса является макроскопической теорией, что предполагает возможность использования подходов механики сплошной среды. Одним из основополагающих принципов механики является принцип освобождаемости от связей. Он гласит: равновесие тела не изменится, если отбросить связи, приложенные к нему, заменив их реакциями связей. Под реакциями связей подразумеваются силы, с которыми связи действуют на рассматриваемое тело. Рассмотрим равновесие межфазного слоя, т.е. слоя жидкости, ограниченного, с одной стороны, объемной фазой, а с другой – газовой фазой. С позиций механики они являются связями для межфазного слоя. Реакция каждой из связей включает поверхностные силы, равные давлениям сил отталкивания в граничных точках межфазного слоя, и объемные силы, определяемые взаимным притяжением контактирующих сред.
Рассмотрим равновесие межфазного слоя, которому на изотерме соответствует участок V2 ≥ V ≥ V1. Выпишем значения параметров состояния среды в граничных точках межфазного слоя: при V = V1P1 = 0, Pпр1 = Pот1; при V = V2P = Pmin, 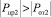 (здесь сравниваются модули величин). Как указывалось в работе [2], силы притяжения образуют класс объемных сил, а значение силы притяжения между двумя взаимодействующими материальными точками может быть представлено в виде [6]
(здесь сравниваются модули величин). Как указывалось в работе [2], силы притяжения образуют класс объемных сил, а значение силы притяжения между двумя взаимодействующими материальными точками может быть представлено в виде [6]
Fпр = m1·m2·f(r), (3)
где m1 и m2 – массы материальных точек; f(r) – некоторая убывающая функция расстояния r между взаимодействующими точками, причем f(r) > 0 при r < R и f(r) = 0 при r ≥ R. Здесь через R обозначен радиус дальнодействия сил межмолекулярного притяжения, равный толщине межфазного слоя. С учетом существенного изменения плотности среды в межфазном слое значение силы притяжения, действующей на частицу межфазного слоя со стороны жидкости, будет значительно больше аналогичной силы, действующей со стороны газовой фазы. В результате сложения этих сил, направленных в противоположные стороны, получим равнодействующую объемных сил притяжения Fоб, направленную в сторону жидкости.
На рис. 2 представлен элемент объема среды, содержащий межфазный слой. Силовые факторы, изображенные на рис. 2, а, с позиций механики являются реакциями связей для межфазного слоя. Так, при мысленном отбрасывании из рассмотрения объемной фазы жидкости ее воздействие на межфазный слой заменяется давлением Pот1 и объемной силой Fоб1. Аналогично отбрасывание газовой фазы предполагает возникновение Pот1 и Fоб2. Очевидно, что объемная сила Fоб = Fоб1 + Fоб2 (жирным шрифтом обозначены векторные величины), т.е. является равнодействующей двух сил притяжения. Рассмотренная схема содержит как поверхностные, так и объемные силовые факторы, что создает определенные проблемы при рассмотрении равновесия.
В теоретической механике используют понятие эквивалентных систем сил. Такими называются две системы сил, которые при замене одной на другую не изменяют состояния объекта, к которому они приложены. Заменив объемную силу Fоб в схеме на рис. 2, а, поверхностной ∆P, получим новую схему нагружения, эквивалентную первоначальной. Очевидно, что равновесие межфазного слоя от такой замены не нарушится. Подобный прием использован при выводе закона Архимеда, в котором поверхностные силы, действующие на тело, погруженное в жидкость, заменялись объемной выталкивающей силой. Условие равновесия для схемы на рис. 2, б примет вид: Pот1 = Pот2 + ∆P2. Отсюда следует, что реакцией системы на внешнее воздействие, направленное на формирование межфазного слоя жидкость-газ, эквивалентно приложению некоторого дополнительного давления ∆P, действующего на границу раздела жидкой и газовой фаз и направленного в сторону объемной фазы жидкости. Такой механизм находится в соответствии с принципом Ле Шателье.
Проведенные рассуждения относились к межфазному слою в целом, что позволило сформулировать условие равновесия на его границе. Далее воспользуемся еще одним фундаментальным принципом механики, который утверждает: если рассматриваемый объект находится в равновесии, то в равновесии пребывает любая часть этого объекта. Отсюда следует, что рассмотренная схема рассуждений справедлива для любой точки М межфазного слоя. В этом случае условие равновесия запишется в виде Pот1 = Pотм + ∆Pм. Записанное уравнение справедливо для произвольной точки изотермы со значением удельного объема Vм, показанной на рис. 1. Характерной особенностью дополнительного давления ∆P является тот факт, что его приложение не сказывается на значении давления в объемной фазе жидкости, которое остается неизменным и равным давлению Pот1.
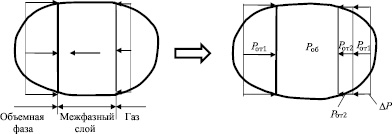
Рис. 2. К равновесию межфазного слоя
Рассмотрение равновесия текучих сред (жидкостей и газов) имеет определенную специфику, отличающую их от твердых тел. В частности, в уравнениях равновесия необходимо предусмотреть выполнение закона Паскаля: давление, производимое на покоящуюся жидкость или газ, передается в любую точку жидкости или газа одинаково по всем направлениям. В соответствии с этим определением давление как одна из компонент тензора напряжений, должно быть одинаковым для всех площадок проходящих через данную точку. Выполнение этого требования возможно представлением тензора напряжений в виде суммы шаровой и девиаторной частей [1].
Рассмотрим тензор напряжений с главными напряжениями σxx, σyy, σzz. Каждая из этих компонент тензора может быть представлена в виде
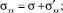
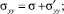
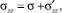
где σ – шаровая часть тензора, а напряжения со штрихами – его девиаторные компоненты. Шаровая часть тензора определяется как
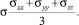 (4)
(4)
Сумма нормальных напряжений является инвариантом тензора, т.е. одинакова для всех площадок, проходящих через точку. Таким образом, шаровая часть тензора может рассматриваться как давление сил отталкивания в уравнении Ван-дер-Ваальса, удовлетворяющее закону Паскаля. Девиаторные компоненты тензора определяют из условия равенства нулю их алгебраической суммы
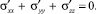 (5)
(5)
Переходя к распределению межфазных напряжений по толщине межфазного слоя, отметим, что задача осесимметрична относительно оси Z, перпендикулярной межфазному слою. Отсюда следует, что σxx = σyy, а компонента тензора σzz из условий механического равновесия постоянна по толщине слоя и равна σxx = Pот1 (см. рис. 2, б). С учетом изложенного, получим
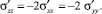 (6)
(6)
Решая совместно уравнения (4)–(6), определим девиаторные компоненты тензора
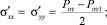
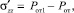 (7)
(7)
где Pот – давление сил отталкивания в произвольной точке межфазного слоя, определяемое из уравнения Ван-дер-Ваальса.
Из рис. 1 следует, что на рассматриваемом участке изотермы 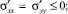 а
а 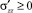 . В соответствии с правилом знаков, используемым в теории Ван-дер-Ваальса, положительными напряжениями считаются сжимающие напряжения. Таким образом, девиаторные компоненты тензора
. В соответствии с правилом знаков, используемым в теории Ван-дер-Ваальса, положительными напряжениями считаются сжимающие напряжения. Таким образом, девиаторные компоненты тензора 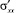 и
и 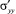 являются растягивающими напряжениями, формирующими поверхностное натяжение на границе раздела жидкость – газ. По существующим представлениям [6] поверхностное натяжение жидкости может быть выражено в виде
являются растягивающими напряжениями, формирующими поверхностное натяжение на границе раздела жидкость – газ. По существующим представлениям [6] поверхностное натяжение жидкости может быть выражено в виде
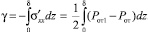 (8)
(8)
Знак минус перед интегралом взят для исключения получения отрицательных значений поверхностного натяжения.
Представление тензора напряжений в виде суммы шаровой и девиаторных частей требует уточнения некоторых положений, использованных в ходе рассуждений. Это связано с тем, что в теории Ван-дер-Ваальса не учитывается разницы между объемными и поверхностными силами, а силовые факторы фигурируют как давления сил притяжения и отталкивания, т.е. формально относятся к классу поверхностных сил. Такой подход справедлив при описании состояния среды в объемной фазе, но неприемлем для описания межфазных взаимодействий.
Дополнительное давление ∆P, введенное в рассмотрение на рис. 2, в соответствии с новым представлением тензора является девиаторной компонентой тензора напряжений 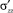 . Действительно для выполнения условий равновесия достаточно приложения только одной из компонент тензора, а значение давления Pот2 в точке на границе межфазного слоя и газовой фазы остается неизменным, отвечающим уравнению состояния при данном значении удельного объема. Такая добавка, являющаяся девиаторной компонентой тензора, не скажется на значении давления, но приведет к появлению дополнительных компонент девиатора
. Действительно для выполнения условий равновесия достаточно приложения только одной из компонент тензора, а значение давления Pот2 в точке на границе межфазного слоя и газовой фазы остается неизменным, отвечающим уравнению состояния при данном значении удельного объема. Такая добавка, являющаяся девиаторной компонентой тензора, не скажется на значении давления, но приведет к появлению дополнительных компонент девиатора 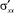 и
и 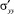 , формирующих межфазное поверхностное натяжение. В рассматриваемом случае газовая фаза воздействует на межфазный слой как отталкивающий магнит.
, формирующих межфазное поверхностное натяжение. В рассматриваемом случае газовая фаза воздействует на межфазный слой как отталкивающий магнит.
В заключение отметим, что все рассмотренные в работе силовые факторы определяют внутреннее состояние среды и, как правило, не поддаются непосредственному измерению. Их внешнее проявление возможно лишь в определенных специфических условиях, например, в известных поверхностных эффектах (смачивание, капиллярные явления, структурирование жидкости в тонких слоях и т.п.).
Рецензенты:
Епархин О.М., д.т.н., профессор, директор, Ярославский филиал ГОУ ВПО «Московский государственный университет путей сообщения», г. Ярославль;
Бачурин В.И., д.ф.-м.н., профессор кафедры высшей и прикладной математики, Ярославский филиал ГОУ ВПО «Московский государственный университет путей сообщения», г. Ярославль;
Виноградова М.Г., д.х.н., профессор кафедры естественнонаучных дисциплин, Тверской институт экологии и права, г. Тверь.
Работа поступила в редакцию 30.12.2013.



