Затопленная струя жидкости является классическим объектом исследования автомодельных асимптотических решений [1]. Несмотря на большой интерес к струйным потокам со стороны исследователей, некоторые вопросы учета взаимодействия струй с окружающей более плотной жидкой средой до сих пор четко не проработаны [5].
Изучение затопленных потоков весьма актуально в рамках проблемы охраны прибрежной и шельфовой зоны морей от загрязнения [6]. Возможные масштабы загрязнения водоемов зависят от поля скоростей самих водоемов, глубины залегания трубопроводов, размеров и характера разрывов, а также от интенсивности выбросов и свойств этих жидкостей [2]. Моделирование струи используется для создания математических моделей устройств, предназначенных для сбора нефтепродуктов при их разливе [3,4].
При истечении струи в жидкость изменению подвергаются следующие параметры: скорость течения, температура, концентрация примеси, при этом возникают вихри, движущиеся вдоль и поперек потока, и между соседними струями происходит обмен конечными массами. На границе двух струй формируется область конечной толщины с непрерывным распределением скорости, температуры и концентрации примеси.
§1. Приближенная модель течения затопленной струи
Рассмотрим следующую задачу. Пусть на дне океана из устья скважины вытекает смесь нефти и газа. Предположим, что известны объемные расходы, теплофизические параметры нефти, газа и окружающей воды. Требуется произвести расчет параметров многофазной струи.
Рассмотрим распределение температуры нефти и газа в струе. Предположим, что капли нефти, пузырьки газа и вода, вовлекаемая в струю, имеют одинаковые температуру, скорость и траекторию в каждом сечении струи. Ось z направлена вертикально вверх. При расчетах используем методику, предложенную в [7].
Начальная площадь поперечного сечения струи:
,
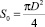где D = 2B0, B0 – радиус скважины.
Скорость течения смеси определим как
, 
,
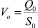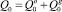здесь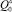 
, 
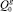– начальные объемные расходы нефти и газа.
Удельный поток импульса на устье: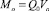 
.
Сила плавучести на единицу массы представляется в виде:
,
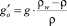где ρw – плотность окружающей воды; ρ – плотность истекающей смеси; g – ускорение свободного падения.
Удельный поток плавучести:
.
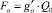Расстояние, на котором удельный импульс силы плавучести превышает удельный импульс, приобретаемый струей вначале:
.
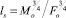Время для перемещения объема жидкости на расстояние z:
.
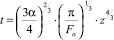Радиус струи на высоте z представляется в виде
.
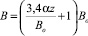Скорость подъема струи в сечении z:
.
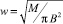Объемный расход представим в следующем виде: Q = πwB2.
Таким образом, можно определить температуру в любом сечении струи, считая, что температура в сечении струи одинаковая и зависит только от координаты z:
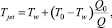
где Tw, T0 – температуры окружающей воды и вытекающей жидкости; Q0 – начальный объемный расход.
Далее представлены зависимости параметров струи от высоты z, полученные на основе численного решения. Для параметров расчета приняты следующие значения:
B0 = 1,7 м, Tw = 4 °C, T0 = 80 °C,
Q0 = 1 м3/с, α = 0,149.
На рис. 1 представлена зависимость температуры струи от вертикальной координаты z. Видно, что на расстоянии z = 10 м температура струи остывает до значения Tjet = 7 °C. При давлении 150 атм. равновесная температура гидратообразования составляет 21 °C. Температура струи опускается ниже равновесной при z = 2,4 м, что говорит о том, что выше данной координаты пузырьки газа начинают покрываться газогидратной коркой.
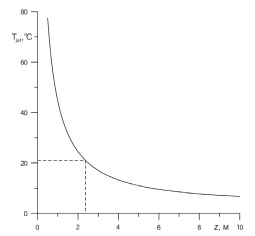
Рис. 1. Зависимость температуры струи от вертикальной координаты для 1 модели
На рис. 2 представлена зависимость скорости струи от высоты z. Видно, что до значения z = 6 м скорость струи растет, затем происходит уменьшение скорости струи из-за утяжеления струи вследствие «вовлекаемой» в струю окружающей воды.
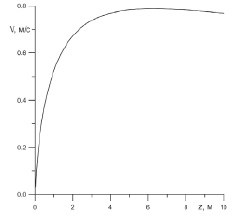
Рис. 2. Зависимость скорости струи от вертикальной координаты для 1 модели
§2. Численная модель расчета параметров струи
Идея модели основана на методе конечных объемов и описана в [7]. Считается, что струя состоит из последовательных (uk, υk, ωk), при этом скорость определяется как (xk, yk, zk)
,
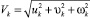здесь (uk, υk) − горизонтальные составляющие скорости, (ωk) вертикальная составляющая скорости.
Угол между осью струи и горизонтальной плоскостью обозначим как φk, а угол между осью х и проекцией оси струи на горизонтальную плоскость через θk.
Радиус струи – Bk, высота элемента в данный момент времени − Hk, масса элемента
.
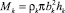Дополнительно используют следующие характеристики среды: температура Tk и плотность ρk.
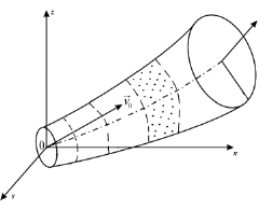
Рис. 3. Схема метода конечных объемов
Применяя уравнения сохранения массы, горизонтального и вертикального импульсов, энергии, а также учитывая увеличение массы на каждом шаге за счет увлечения воды и вихревого течения, получаем следующую численную модель. В этих уравнениях пренебрегаем сопротивлением окружающей воды и не учитываем скорость окружающей среды, считая ее покоящейся.
;
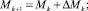
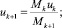
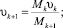
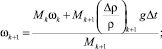
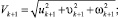
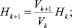
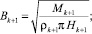
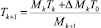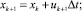
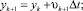
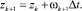
Начальные условия:
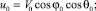
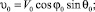
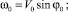
B0 = H0;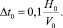 
В данном случае предполагаем, что приход массы есть постоянная величина на каждом шаге и определяется как доля от массы элемента на предыдущем шаге. В дальнейшем модель предполагается улучшить за счет расчета поступающей массы, учитывая захват воды за счет смешивания, увлечения и вихревого течения самого потока.
Далее представлены зависимости параметров струи от высоты z, полученные на основе представленного численного решения. Для параметров расчета приняты следующие значения: V0 = 0,3 м/с, φ0 = 90°, θ0 = 0°, B0 = 0,2 м, T0ср = 4 °С, T0ст = 80 °С.
На рис. 4 представлена зависимость температуры струи от координаты z. Температура струи опускается с 80 °C до 4 °C, т.е. до температуры окружающей среды. При z = 3 м температура струи остывает до равновесной температуры гидратообразования, что говорит о том, что выше данной координаты пузырьки газа начинают покрываться газогидратной коркой.
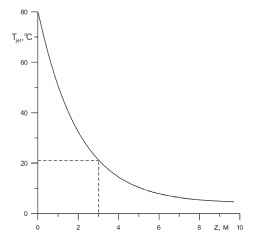
Рис. 4. Зависимость температуры струи от вертикальной координаты для 2 модели
На рис. 5 приведена зависимость скорости струи от вертикальной координаты. При z = 4,5 м скорость струи становится постоянной.
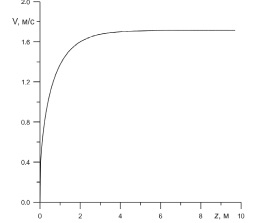
Рис. 5. Зависимость скорости струи от вертикальной координаты для 2 модели
Выводы
В работе представлены две модели затопленных струй, проведены расчеты теплофизических и кинематических параметров, получены графики зависимости температуры и скорости от вертикальной координаты. Вследствие «захвата» окружающей воды струей происходит охлаждение струи до температуры окружающей среды. Для каждой модели определены характерные координаты, выше которых наступает условие гидратообразования. С ростом вертикальной координаты увеличение скорости струи замедляется, что вызвано увеличением массы струи.
Рецензенты:
Михайлов П.Н., д.ф.-м.н., профессор, заведующий кафедры «Алгебра и геометрия» Стерлитамакского филиала, ФГБОУ ВПО «Башкирский государственный университет», г. Стерлитамак;
Мустафина С.А., д.ф.-м.н., профессор, заведующая кафедры «Математическое моделирование», декан физико-математического факультета Стерлитамакского филиала, ФГБОУ ВПО «Башкирский государственный университет», г. Стерлитамак.
Работа поступила в редакцию 30.12.2013.