Занятия спортом имеют важное значение для сохранения здоровья и трудоспособности человека. Рост экстремальных видов спорта, характерный для современности, выдвигает на передний план задачу целенаправленного улучшения ассортимента и качества спортивной одежды, которая занимает особое место в комплексе мероприятий по обеспечению успешной и безопасной деятельности спортсменов. Необходимость системного подхода к проектированию спортивной одежды объективно обусловлена тем, что одежда является одним из звеньев в системе «человек – одежда – окружающая среда». Оптимизация этой системы требует точной информации о биомеханических параметрах, и невыполнение этого требования влечет за собой в лучшем случае снижение эффективности системы в целом, а в худшем – потерю «прочности» ее важнейшего, человеческого звена [7].
Сопряженность элементов системы «человек-одежда» в первую очередь определяется антропометрическим соответствием изделия размерам и форме тела человека при выполнении им различных видов движений [1].
Целью данной работы является получение регрессионных моделей изменения линейных параметров (размерных признаков тела человека) при изменении амплитуды движения в основных суставах на основе изучение биомеханики двигательных процессов. Полученная информация является исходной при выборе конструктивно-технического решения одежды для экстремальных видов спорта, связанных с высокой динамикой движения.
Материалы и методы исследований
Объектом исследования является процесс объективизации выбора проектного решения спортивной одежды. При выполнении работы были использованы методология системного подхода к проектированию специальной одежды, методы математической статистики и регрессионного анализа, методы динамической антропометрии.
Результаты исследования и их обсуждение
В ранее проведенных исследованиях уже была получена математическая модель зависимости изменения размерных признаков от углов амплитуды движения в основных суставах [4]. Однако эти значения справедливы при наличии открытого контура одежды, а значит, обеспечения динамики движения за счет дополнительного резерва, например, перемещения низа изделия и низа рукава. По результатам анализа потребительских предпочтений, выполненного на основе анкетного опроса спортсменов, занимающихся экстремальными видами спорта (альпинизм, горные лыжи и т.п.), установлена необходимость включения в ассортимент проектируемых изделий мужского комбинезона [5]. Исследования были проведены на примере разработки комбинезона для спортсменов-альпинистов по предложению туристического центра «Горизонт-Экстрим» г. Благовещенска. Конструктивным отличием комбинезона от других видов одежды является наличие замкнутого контура изделия от линии обхвата шеи (или от точки метопион при наличии капюшона) до уровня пяточной точки, поэтому обеспечение динамического соответствия конструкции осуществляется только за счет внутреннего резерва.
Изменение размеров тела человека при движении определяют методом динамической антропометрии [3]. Особенность проведения биокинематических исследований для реализации поставленной цели работы заключалась в том, что спортсмен в процессе восхождения должен принимать определенную позу, регламентируемую техническими приемами альпинизма, поэтому в программу измерений были включены комплексные значения угловых параметров, характеризующих наиболее экстремальные виды движений (поз). На рисунке представлен пример характерной позы, буквами обозначены измеряемые углы амплитуды в основных суставах.
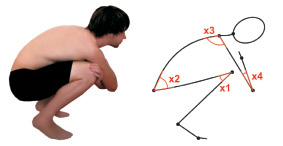
Динамическая поза № 1 «Сгибание (разгибание) ноги в коленном суставе (X1) при одновременном наклоне туловища (X2)»
Программа антроподинамических исследований включала 14 размерных признаков, выбранных с учетом их максимальной изменчивости для установленных видов движений. Диапазоны варьирования сочетания углов движений в суставах устанавливались между максимальными и минимальными значениями угловых параметров движений, которые были выбраны с учетом физических возможностей человека фиксировать определенное положение туловища и конечностей.
В ряде исследований [3] было установлено, что биологическая компонента существенно превышает ошибку измерения, поэтому величины динамических эффектов рассчитывались в относительных значениях по по формуле
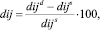 (1)
(1)
где dij – относительный динамический эффект i-го размерного признака у j-й фигуры (j = 1, 2,…, 100), %; dijd, dijs – величины i-го размерного признака в динамическом и статическом (соответственно) положении j-й фигуры, см.
Для получения зависимостей между показателями Y (относительного динамического эффекта i-го размерного признака) и X (величин углов амплитуды) использовались методы регрессионного анализа, в том числе линейные и нелинейные функции множественной регрессии [2].
Предложенные модели имеют вид линейной функции множественной регрессии:
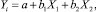 (2)
(2)
или квадратичной нелинейной регрессии:
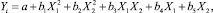 (3)
(3)
где Yi – зависимая величина; X1, X2 – независимые переменные; a, b1, b2, b3, b4, b5 – искомые коэффициенты.
В случае если линейная функция не дает стабильных результатов, то рекомендуется использовать одну из нелинейных функций регрессии.
Параметры при переменной X называются коэффициентами «чистой» регрессии. Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизменном значении других факторов, закрепленном на среднем уровне.
Для проверки качества построенной модели использовался F-критерий Фишера и t-критерий Стьюдента. При этом модель считалась качественной, если значимость F-критерия Фишера меньше 0,05. Чем меньше данный коэффициент, тем модель точнее. Полученные соотношения тестировались для уровня доверия 95 %.
Формула для расчета F-критерия Фишера:
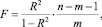 (4)
(4)
где n – число единиц совокупности; m – число параметров при переменных Х; R2 – коэффициент детерминации.
Fтабл – максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости a. Уровень значимости a – вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно a принимается равной 0,05.
Если Fтабл < Fфакт , то Но – гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если Fтабл > Fфакт , то гипотеза Но не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии [8].
Аппроксимация экспериментальных зависимостей динамических эффектов от угловых биомеханических параметров движений тела человека позволила найти значения коэффициентов множественной регрессии статистических характеристик для линейных и нелинейных математических моделей.
Например, полученная регрессионная модель динамического эффекта размерного признака Д1 «длина спины до талии» для сгибания (разгибания) ноги в коленном суставе при одновременном наклоне туловища:
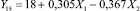
позволяет определить величину относительного динамического эффекта при любом угле сгибания ноги в коленном и туловища в тазобедренном суставах, заданном в пределах варьирования амплитуды этого движения. Например, для сгибания (разгибания) ноги в коленном суставе на величину угла X1 = 30° при одновременном наклоне туловища на величину угла X2 = 40° динамический эффект размерного признака «длина спины до талии» составит 12,2 % статического значения этого признака. Регрессионные модели зависимости относительных динамических эффектов размерных признаков от угловых биомеханических параметров представлены в таблице.
Получение зависимостей между динамическими эффектами и угловыми параметрами движений дают возможность использования угловых биомеханических параметров в качестве информативных исходных данных для целенаправленного обеспечения динамического соответствия конструкции одежды.
Заключение
Выявлена необходимость проведения биокинематических исследований для выбора конструктивных параметров при проектировании изделий, имеющих замкнутый контур. Для этого разработана программа динамической антропометрии определения динамических эффектов в наиболее экстремальных по виду движения позах. Полученные математические модели имеют вид множественной регрессии или квадратичной нелинейной регрессии: изменения размерных признаков в динамике в зависимости от изменения углов амплитуды сегментов верхних и нижних конечностей. Представленная совокупность исходных данных, характеризующих изменение размеров и формы тела человека для установленных видов движения, составляет наряду с традиционно используемой информацией основу для выбора конструктивных средств обеспечения динамического соответствия в одежде.
Регрессионные модели зависимости относительных динамических эффектов размерных признаков от угловых биомеханических параметров
|
Размерный признак |
Усл. обозн. динам. эффекта |
Уравнение регрессионной модели |
Критерий Фишера |
|
1 |
2 |
3 |
4 |
|
Наклон туловища с горизонтальным отведением (приведением) рук в плечевом суставе |
|||
|
Длина спины до талии |
d′1 |
Y1 = 2,324 + 0,01599Х7 + 0,047Х8 |
0,00189556 |
|
Расстояние от линии талии до подъягодичной складки |
d′2 |
Y2 = –3,321 + 0,0562Х7 + 0,2919Х8 |
0,000123 |
|
Расстояние от линии талии сзади до середины подколенной ямки |
d′3 |
Y3 = 1,877 + 0,007469Х7 + 0,161Х8 |
0,000018 |
|
Расстояние от линии талии до пяточной точки |
d′4 |
Y4 = 1,1388 + 0,003373Х7 + 0,0883Х8 |
0,000019 |
|
Расстояние от шейной до пяточной точки |
d′5 |
Y5 = 1,443 + 0,007229Х7 + 0,076386Х8 |
0,000021 |
|
Ширина спины |
d12 |
Y6 = 15,18 + 0,000007Х72 – 0,004Х82 – 0,000026X1X2 + 0,749X8 |
0,0479 |
|
Высота плеча косая |
d13 |
Y7 = 8,598 – 0,0176Х7 + 0,1038Х8 |
0,01358 |
|
Сгибание (разгибание) руки в плечевом и локтевом суставе при одновременном наклоне туловища |
|||
|
Расстояние от линии талии до заднего угла подмышечной впадины |
d6 |
Y8 = –79,46 + 0,657Х3 + 0,353Х4 |
0,00005400 |
|
Расстояние от заднего угла подмышечной впадины до локтя |
d7 |
Y9 = 33,11 + 0,0418Х3 + 0,185Х4 |
0,0000851 |
|
Расстояние от заднего угла подмышечной впадины до запястья |
d8 |
Y10 = 20,45 + 0,073Х1 – 0,138Х4 |
0,00072172 |
|
Расстояние от линии талии через задний угол подмышечной впадины до запястья |
d9 |
Y11 = 0,845 + 0,189Х3 – 0,0461Х4 |
0,000109 |
|
Отведение (приведение) ноги вертикальное в тазобедренном суставе при одновременном сгибании (разгибании) ноги в коленном суставе |
|||
|
Расстояние от линии талии сзади до подъягодичной складки |
d′2 |
Y12 = 21,57 – 0,00602Х5 – 0,1383Х6 |
0,000033 |
|
Длина ноги по внутренней поверхности от точки промежности до верхнеберцовой внутренней точки |
d10 |
Y13 = –20,84 + 0,837Х5 + 0,1206Х6 |
0,000644 |
|
Длина ноги по внутренней поверхности от точки промежности до низа стопы |
d11 |
Y14 = 7, 773 + 0,319Х5 + 0,0264Х6 |
0,00189556 |
|
Cгибание (разгибание) ноги в коленном суставе при одновременном наклоне туловища |
|||
|
Длина спины до талии |
d1 |
Y15 = 18 + 0,305Х1 – 0,367Х2 |
0,0000305 |
|
Расстояние от линии талии до подъягодичной складки |
d2 |
Y16 = 52 + 1,828Х1 + 1,305Х2 |
0,001657293 |
|
Расстояние от линии талии сзади до середины подколенной ямки |
d3 |
Y17 = 0,58 + 0,0748Х1 + 0,068Х2 |
0,00000246 |
|
Расстояние от шейной до пяточной точки |
d5 |
Y18 = 10,22 + 0,392Х1 – 0,394Х2 |
0,013053 |
|
Наклон шеи и головы вперед (седьмой и первый шейный позвонок) |
|||
|
Дуга головы |
d14 |
Y19 = 12,229 – 0,01358Х7 – 0,0801Х8 |
0,75 |
Рецензенты:
Бойцова Т.М., д.т.н., профессор, директор института сервиса, туризма и дизайна Владивостокского государственного университета экономики и сервиса, г. Владивосток;
Шеромова И.А., д.т.н., профессор кафедры сервисных технологий Владивостокского государственного университета экономики и сервиса, г. Владивосток.
Работа поступила в редакцию 25.12.2013.



