Появление нетранзитивных включений в результатах определения весовых коэффициентов показателей качества пищевых продуктов ставит задачу исключения нетранзитивных включений.
Контроль качества пищевых продуктов проводится по ряду таких органолептических показателей, как вкус, цвет, запах и т.п. Оценка же качества продукта проводится по комплексному показателю, который в большинстве случаев определяют по среднему арифметическому взвешенному с учетом весовых коэффициентов. В этом случае весовые коэффициенты показателей качества пищевых продуктов определяются различными методами: ранжирования, попарного сопоставления и двойного попарного сопоставления [3,6]. Практика применения этих методов при определении весовых коэффициентов показывает, что в любом случае возможно появление нетранзитивных включений [4, 5].
Целью данного исследования является исключение нетранзитивных подмножеств из результатов определения весовых коэффициентов показателей качества хлебобулочных изделий методом Кемени.
Материалы и методы исследования
Метод исследования – экспериментальный и аналитический.
Идея Джона Кемени. Согласно идее Дж. Кемени, для решения задачи исключения нетранзитивности надо минимизировать суммарное расстояние от кандидата в средние до мнений экспертов. Найденное таким способом среднее мнение называют «медианой Кемени».
С помощью расстояния Кемени находят итоговое мнение экспертной комиссии. Пусть А1, А2, А3, …, Ар – ответы р экспертов, представленные в виде бинарных отношений. Для их усреднения используют медиану Кемени [1, 2].
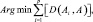 (1)
(1)
где Arg min – то или те значения А, при которых достигает минимума указанная сумма расстояний Кемени от ответов экспертов до текущей переменной А, по которой и проводится минимизация.
Таким образом,
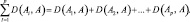 (2)
(2)
Для арифметического нахождения медианы Кемени используют вертикальную форму записи ранжирований.
При этом для заполнения матрицы отношения предпочтения необходимо произвести следующее преобразование [6]:
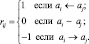 (3)
(3)
Результаты исследования и их обсуждение
При работе дегустационной комиссии на ОАО «Бурятхлебпром» были получены следующие результаты определения весовых коэффициентов показателей качества первого сорта методом ранжирования (табл. 1).
Свертка по результатам табл. 1 будет иметь вид:
б → а → в ~ г ~ д,
где знак «→» означает предпочтение следующего за знаком объекта, чем предшествующего перед ним; знак «~»означает равнозначность объектов.
Таблица 1
Результаты определения весовых коэффициентов показателей качества хлеба первого сорта, полученные методом ранжирования
|
а) Форма |
б) Поверхность |
в) Состояние мякиша |
г) Запах |
д) Вкус |
|
|
1 эксперт |
2 |
1 |
5 |
3 |
4 |
|
2 эксперт |
2 |
1 |
4 |
3 |
5 |
|
3 эксперт |
1 |
2 |
3 |
5 |
4 |
|
4 эксперт |
2 |
1 |
4 |
5 |
3 |
|
5 эксперт |
1 |
2 |
4 |
3 |
5 |
|
6 эксперт |
1 |
2 |
5 |
4 |
3 |
|
7 эксперт |
2 |
1 |
3 |
5 |
4 |
|
Сумма |
11 |
10 |
28 |
28 |
28 |
Здесь показано, что показатели качества в, г, д получили по 28 баллов и они равнозначны, но они предпочтительнее а, который в свою очередь предпочтительнее б.
Ранжирование каждого эксперта также можно расписать в виде сверток:
1 эксперт: б → а → г → д → в;
2 эксперт: б → а → г → в → д;
3 эксперт: а → б → в → д → г;
4 эксперт: б → а → д → в → г;
5 эксперт: а → б → г → в → д;
6 эксперт: а → б → д → г → в;
7 эксперт: б → а → в → д → г.
Для нахождения медианы Кемени мнения экспертов в виде ранжированного ряда преобразованы согласно выражению (3) и построены матрицы отношений.




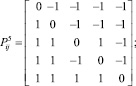


Расстояние между каждыми двумя матрицами будет равно:
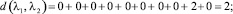
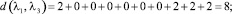
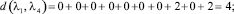
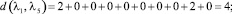
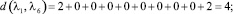
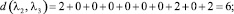
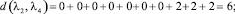
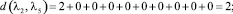
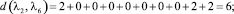
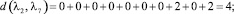
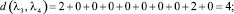
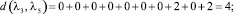
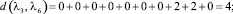
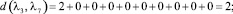
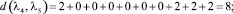
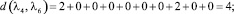
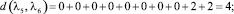
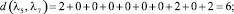
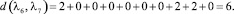
Все полученные данные заносим в матрицу расстояний (табл. 2).
Из всех вычисленных сумм наименьшая равна 26, и достигается она при А2. Следовательно, медиана Кемени – это мнение 2 эксперта. Это значит, что мнение 2 эксперта находится ближе ко всем остальным мнениям.
Поэтому мнение 2 эксперта принимается за результирующее мнение всей экспертной комиссии.
Таблица 2
Матрица расстояний
|
A1 |
А2 |
А3 |
А4 |
А5 |
А6 |
А7 |
∑ |
|
|
А1 |
0 |
2 |
8 |
4 |
4 |
4 |
6 |
28 |
|
А2 |
2 |
0 |
6 |
6 |
2 |
6 |
4 |
26 |
|
А3 |
8 |
6 |
0 |
4 |
4 |
4 |
2 |
30 |
|
А4 |
4 |
6 |
4 |
0 |
8 |
4 |
2 |
28 |
|
А5 |
4 |
2 |
4 |
8 |
0 |
4 |
6 |
28 |
|
А6 |
4 |
6 |
4 |
4 |
4 |
0 |
6 |
28 |
|
А7 |
6 |
4 |
2 |
2 |
6 |
8 |
0 |
28 |
Выводы
Следовательно, метод Кемени, используемый для исключения нетранзитивных подмножеств, полученных при голосовании, может быть распространен для исключения нетранзитивных включений, полученных при определении весовых коэффициентов качества продукции и услуг методом ранжирования.
Рецензенты:
Лабаров Д.Б., д.т.н., профессор, заслуженный работник высшей школы РФ, декан инженерного факультета, Министерство образования и науки Российской Федерации, ФГБОУ ВПО «Бурятская государственная сельскохозяйственная академия им. В.Р. Филиппова», г. Улан-Удэ;
Дамдинов Б.Б., д.ф-м.н., доцент кафедры «Общая физика»; Министерство образования и науки Российской Федерации, ФГБОУ ВПО «Бурятский государственный университет», г. Улан-Удэ.
Работа поступила в редакцию 10.12.2013.



