Современный кривошипный горячештамповочный пресс (рис. 1) – изделие, подвижные детали и узлы которого массой от сотен килограмм до нескольких тонн в процессе работы циклически перемещаются со скоростями, соответствующими десяткам оборотов главного вала в минуту, при технологических нагрузках на исполнительном звене (ползуне) достигающих десятков меганьютонов. Оценка способности пресса к выполнению конкретного технологического процесса горячей объёмной штамповки (ГОШ) осуществляется, как правило, на основании графика допустимых усилий на его ползуне [1] без учёта возникающих при этом динамических нагрузок, в то время как их влияние на работоспособность и долговечность узлов пресса не вызывает сомнений и подтверждена рядом исследований [2–4].
В известных работах, посвящённых анализу динамических процессов в КГШП, его механизмы моделируются многомассовыми колебательными системами, позволяющими рассчитать нагрузки, связанные с крутильными колебаниями валов и растяжением-сжатием шатуна, ползуна и станины пресса [2–4]. Однако при штамповке на КГШП максимальные нагрузки возникают в конце рабочего хода ползуна, когда вращающая составляющая усилия со стороны ползуна на главный вал пресса минимальна. На этом временном отрезке элементы пресса: станина, шатун и ползун испытывают преимущественно деформации растяжения-сжатия, а главный вал работает на изгиб. В течение остального времени схема нагружения главного вала – кручение и изгиб. Очевидно, что при моделировании динамических процессов, протекающих в КГШП, необходимо учитывать эти особенности.
Динамическая модель [4], представляющая собой систему сосредоточенных масс, соединённых упруго-диссипативными связями, приведена на рис. 2. Основное отличие данной модели от уже известных [2–4] ‒ возможность исследования колебательных процессов в КГШП как с учётом крутильных деформаций валов, растяжения-сжатия шатуна, ползуна, станины пресса, так и изгибных колебаний его главного вала.
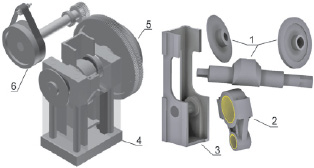
а б
Рис. 1. Твердотельная модель КГШП модели К8544: а – в сборе, б – главный вал и детали кривошипно-ползунного механизма; 1 – главный (эксцентриковый) вал и диски тормоза и муфты; 2 – шатун; 3 – ползун; 4 – станина; 5 – муфта; 6 – привод
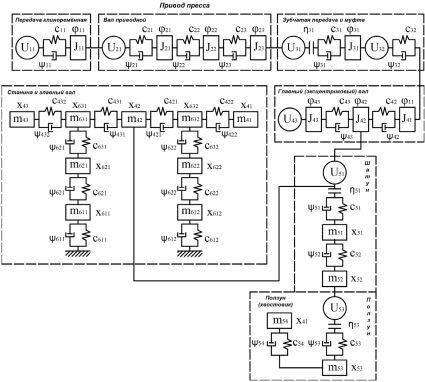
Рис. 2. Динамическая модель КГШП: Jmn, mmn – моменты инерции и массы, cmn, ψmn – жёсткости и коэффициенты диссипации, ηmn – зазоры в кинематических парах, Umn – функции положения, φmn, xmn – перемещения, где m = 1...6 – номер механизма, n – номер массы механизма
Структура и основные характеристики динамической модели следующие:
1. Электродвигатель – маховик, связанные клиноремённой передачей. Одномассовая динамическая модель (m = 1, n = 1). Функция положения U11 = ω·t, где ω = const – угловая скорость электродвигателя.
2. Вал приводной – трёхмассовая динамическая модель (m = 2, n = 3).
3. Муфта (зубчатое колесо, постоянно вращающиеся детали фрикционной муфты, диск муфты) – двухмассовая динамическая модель (m = 3, n = 2). В зубчатом зацеплении, передаточное отношение которого определяется функцией = φ23, предполагается наличие зазора. Функция положения U32 = φ31 при работе пресса в автоматическом режиме (муфта включена). При работе пресса в режиме одиночных ходов на участке включения муфты предполагается, что ускорение дисков муфты изменяется по синусоидальному закону (1):
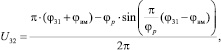 (1)
(1)
где φвм, φр – углы включения и разгона муфты.
На участке торможения имеет место разрыв связи с приводом (c32 = 0, ψ32 = 0).
4. Главный (эксцентриковый) вал – трёхмассовая динамическая модель (m = 4, n = 3). Расчёт крутильных колебаний. Первая масса – участок вала с диском муфты до эксцентрика. Вторая масса – эксцентрик. Третья масса – фрагмент главного вала после эксцентрика и диск тормоза. При работе пресса в автоматическом режиме воздействие тормоза на массу J43 отсутствует (U43 = φ43). При работе пресса в режиме одиночных ходов на участке включения тормоза предполагается изменение ускорения его диска по синусоидальному закону (2):
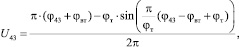 (2)
(2)
где φвт, φт – углы включения тормоза и торможения.
Расчёт изгибных колебаний главного вала выполняется одновременно с расчётом колебательных процессов в станине.
5. Кривошипно-ползунный механизм – четырёхмассовая динамическая модель (m = 5, n = 4). Шатун – двухмассовая динамическая модель. Предполагается, что шатун работает только на растяжение-сжатие. Жёсткости шатуна на растяжение и сжатие различны. Ползун – двухмассовая динамическая модель. Первая масса ‒ сам ползун, вторая – его хвостовик. В соединениях эксцентрик главного вала – шатун и шатун – ползун имеются зазоры. Функция, связывающая положение ползуна и шатуна с углом поворота главного вала U51(φ42), приведена в работах [1, 4], U53 = x52.
6. Станина и главный вал – девятимассовая динамическая модель. Массы m6ni – n = 3, i = 1 – левая стойка станины, i = 2 – правая стойка станины.Деформация растяжение-сжатие. Массы m42 (эксцентрик), m41 (муфта), m43 (тормоз) – главный вал. Деформация растяжение-сжатие и изгиб. Изгиб фрагментов главного вала рассчитывается как линейное отклонение его положения под воздействием сосредоточенной силы.
Движение масс динамической модели (рис. 2), описывается двадцатью двумя обыкновенными, нелинейными, кусочно-непрерывными дифференциальными уравнениями второго порядка (математическая модель), составленными с помощью уравнения Лагранжа 2-го рода с «лишними» координатами [4].
Расчёт упруго-инерционных и диссипативных параметров (cmn, mmn, Jmn, ψmn) осуществляется на основе твердотельной модели пресса (рис. 1) в соответствии с методикой, предложенной в работах [4, 5].
На рис. 3 представлено основное окно программного решения «Динамика кривошипного пресса» [6], в рамках которого предусмотрена возможность ввода, тестирования и сохранения параметров динамической модели кривошипного пресса и реализуемой с его помощью технологии. Компьютерное моделирование динамики пресса на основе данной программы позволяет решить следующие задачи:
● исследовать влияние конструктивных параметров пресса на уровень протекающих в его элементах динамических процессов, что представляет несомненный интерес при выполнении работ, связанных с проектированием нового и совершенствованием существующего оборудования;
● определить пригодность пресса для выполнения технологического процесса в зависимости от степени износа его кинематических пар;
● выполнить сравнительный анализ возможных технологий изготовления одной и той же поковки с точки зрения их влияния на динамику пресса.
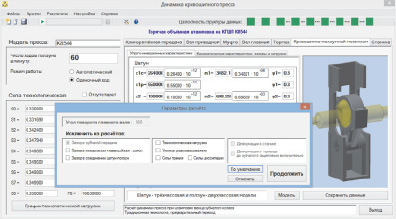
Рис. 3. Определение параметров КГШП и параметров расчёта
На рис. 4 приведено окно результатов компьютерного моделирования динамики пресса К8544 при выполнении им технологической операции предварительной штамповки поковки каретки синхронизатора коробки передач грузового автомобиля КАМАЗ [7].
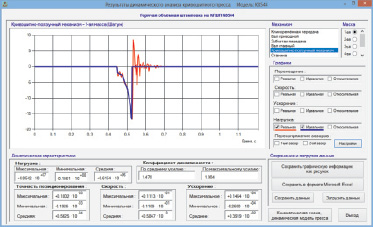
Рис. 4. Результаты динамического анализа КГШП
Уровень динамических процессов в механизме можно оценить:
● путём визуального анализа графиков изменения перемещений, скоростей, ускорений его элементов, связанных с соответствующими массами динамической модели, нагрузками, возникающими при деформации этих элементов, диаграммам пересопряжения зазоров в кинематических парах;
● на основе значений ряда критериев, отражающих общий уровень динамических процессов в исследуемом механизме.
Кроме графическое представление изменения кинематических параметров движения масс модели и нагрузок на них воздействующих, так и рассчитать значения ряда критериев, характеризующих интенсивность динамических процессов в механизмах пресса, основными из которых являются максимальная (Рmax), минимальная (Pmin) и средняя (Рср) нагрузки, коэффициенты динамичности. Учитывая, что элементы пресса в процессе работы испытывают нагрузки различного направления, в дальнейшем будем считать, что деформация и соответствующая ей сила отрицательны, если они возникают в результате приложения к ползуну пресса нагрузки однонаправленной с технологической. Средняя нагрузка рассчитывается в соответствии с выражением (3):
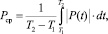 (3)
(3)
где Т1 и Т2 – начальный и конечный моменты отрезка времени, на котором исследуются динамика пресса; P(t) – текущее значение нагрузки.
Традиционно под коэффициентом динамичности понимается отношение максимальных абсолютных величин реального ускорения исследуемого звена механизма к идеальному, рассчитанному только на основе уравнений кинематики. Такой способ расчёта коэффициента динамичности не всегда приемлем для КГШП. Например, при работе пресса в автоматическом режиме идеальное ускорение главного вала равно нулю, соответственно использование коэффициента динамичности теряет смысл. При решении задач, связанных с исследованием влияния на динамику пресса применения различных вариантов технологических схем горячей объёмной штамповки одного и того же изделия, в качестве коэффициентов динамичности предлагается использовать выражения (3) и (4):
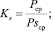 (4)
(4)
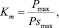 (5)
(5)
где Рср, Рsср, Pmax и Psmax – соответственно средняя динамическая, средняя статическая, максимальные по абсолютной величине динамическая и статическая нагрузки в исследуемом элементе механизма, рассчитанные на временном отрезке [Т1, Т2]. Коэффициент Km определяет относительный уровень максимальной нагрузки в исследуемом механизме (детали, фрагменте детали) пресса и является показателем прочности. Значение Ks зависит от амплитуды, частоты, скорости затухания колебаний и является показателем, определяющим износ и усталостное разрушение.
Рецензенты:Володин И.М., д.т.н., профессор, заведующий кафедрой механики пластического деформирования, Липецкий государственный технический университет, г. Липецк;
Козлов А.М., д.т.н., профессор, заведующий кафедрой технологии машиностроения, Липецкий государственный технический университет, г. Липецк.
Работа поступила в редакцию 05.12.2013.



