В современных условиях значительные объемы нефти и газа добываются на морских месторождениях. Эта добыча производится при помощи морских стационарных платформ (МСП), которые эксплуатируются в сложных климатических условиях, при которых возможно разрушение ее отдельных элементов и узлов, что может вызвать разрушение всей конструкции [1]. Целью данной статьи является изучение напряженного состояния сварных соединений опорного блока МСП, что позволит в дальнейшем провести оценку их ресурса. МСП имеет два вида соединений ‒ соединение двух труб под прямым углом (тавровое, рис. 1) и соединение труб под углом (раскос). В данной статье рассматривается только тавровое соединение, результаты моделирования для второго случая будут приведены в отдельной статье. Для исследования напряженного состояния сварных соединений МСП автором предлагается следующая методика:
1. Численно определить силы и напряжения, возникающие от сил тяжести конструктивных элементов МСП, установленного технологического оборудования и выталкивающей силы водной среды.
2. Определить параметры волн, действующих на данном месторождении при помощи методики, описанной в СП 38.13330.2012, приложение А.
3. Рассчитать нагрузки, возникающие от волнового воздействия в соответствии с приложением Е СП 38.13330.2012.
4. Определить моменты нагрузок от волнового воздействия, действующие в сварном соединении МСП.
5. Определить суммарное напряжение от волновой нагрузки в сечении сварного соединения.
6. Рассчитать сумму напряжений от волновой нагрузки и общего веса конструкции с установленным на ней технологическим оборудованием, с учетом выталкивающей силы и веса морского обрастания.
Проиллюстрируем разработанную методику. Для этого выберем МСП, установленную на Субботинском месторождении. Данное соединение является тавровым и представляет собой горизонтальный элемент выполненный из цилиндрической трубы диаметром 530 мм, врезанный в вертикальную стойку (колонну), которая представляет собой трубу диаметром 720 мм под прямым углом (рис. 1). Согласно данным проекта МСП, сварные соединения выполнены по ГОСТ 16037-80 и представляют собой равнобедренный треугольник с катетами kfz = 1,56 см (рис. 2). При расчете угловых соединений, в том числе тавровых, условно принимается, что вне зависимости от действующей нагрузки эти сварные соединения работают на условный срез. Разрушение происходит по наименьшей площади скольжения шва как при действии изгибающего момента, так и при воздействии продольной или поперечной силы. Расчетное сечение углового шва принимается в виде равнобедренного треугольника, вписанного в сечение сварного шва. Катет треугольника принимается равным высоте шва, и наплывы при этом не учитываются.
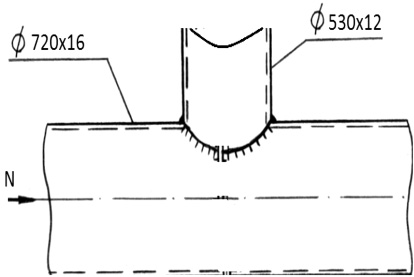
Рис. 1. Соединение горизонтального элемента с колонной
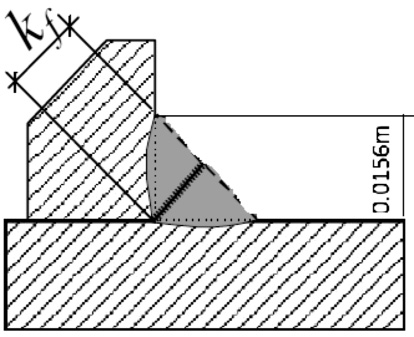
Рис. 2. Тавровое сварное соединение МСП
На это соединение будут действовать силы:
1. Сила Р и ее момент от волнового воздействия на вертикальную колонну (стойку) диаметром 720 мм, направленная перпендикулярно к поверхности стойки.
2. Распределенная сила q и ее момент, вызванные волновым воздействием на горизонтальный элемент диаметром 530 мм, которая направлена перпендикулярно поверхности горизонтального элемента и имеет свои особенности расчета, отличные от расчета волновой нагрузки на вертикальный элемент.
На сварное соединение, так же как и на все конструктивные элементы опорного блока МСП, действуют силы тяжести элементов опорного блока и оборудования, вес морского обрастания, а также Архимедова сила на погруженные в воду элементы. Расчет напряжений в kN/m2 от этих воздействий производился в программном комплекса СКАД по трем сечениям (две околоторцевые поверхности и середина элемента), в результате чего были получены следующие результаты (табл. 1).
Из табл. 1 становится очевидно, что максимальные напряжения порядка 1042 kN/m2 возникают в вертикальной колонне и увеличиваются по мере возрастания глубины, и имеют тоже направление. Для горизонтальных элементов величина возникающих от указанных сил напряжений незначительна, а для раскосов она составляет приблизительно 25 % от величины напряжений, возникающих в вертикальной колонне напряжений. Заменим известные величины напряжений в вертикальной стойке сосредоточенной силой. Исходя из того, что площадь поперечного сечения колонны диаметром 720 мм и толщиной стенки 16 мм составит 0,071 м2, а как это широко известно, напряжение является силой действующей на некотором участке площади, то получим равнодействующую силу N = 74,54 kN. Определим суммарное напряжение, возникающее в сварном соединении при действии сил тяжести и выталкивающей силы и ее момента по формуле
![]() (1)
(1)
где МN – момент силы от действия суммарной нагрузки; N – равнодействующая сила; L – длина шва; kfz – катет шва, который должен быть не менее 6 мм, а в соответствии с ГОСТ 16037-80 принимается равным 1,3 толщины более тонкой детали. С учетом того, что толщина трубы диаметром 530 мм составляет 12 мм, получаем 12·1,3 = 15,6 мм = 0,0156 м; βzf – коэффициент, зависящий от вида сварки, положения сварного соединения, катета сварного шва и выбора метода расчета (т.е. по металлу границы сплавления или металлу сварного соединения), принятый в соответствии с [3] βzf = 0,9. Исследуемое нами сварное соединение представляет собой вертикальную колонну диаметром 720 мм, подверженную совместному волновому и ветровому воздействию, соединенную с горизонтальным элементом диаметром 530 мм, подвергаемой тем же воздействиям. Однако ввиду разницы в особенностях расчета волновой нагрузки на горизонтальные и вертикальные элементы, а также разнице в диаметрах на сварной шов будут воздействовать разные по величине и направлению нагрузки.
Таблица 1
Выписка из протокола расчета напряжений опорного блока МСП «Субботино»
|
Сечение |
N, kN/m2 |
Mk, kN·m |
My, kN·m |
Qz, kN/m2 |
Mz, kN·m |
Qy, kN/m2 |
|
Колонна (стойка) 720×16 |
||||||
|
№ 1 |
–1006,41 |
0,26 |
6,60 |
1,56 |
6,41 |
0,81 |
|
№ 2 |
–1024,67 |
0,26 |
8,58 |
–0,83 |
2,00 |
0,81 |
|
№ 3 |
–1042,80 |
0,26 |
–2,48 |
–3,23 |
–2,41 |
0,81 |
|
Горизонтальный элемент 530×12 |
||||||
|
№ 1 |
0,07 |
0,17 |
–2,77 |
2,84 |
–0,07 |
–0,04 |
|
№ 2 |
0,07 |
0,17 |
1,68 |
0,12 |
0,03 |
–0,04 |
|
№ 3 |
0,07 |
0,17 |
–2,04 |
–2,60 |
0,14 |
–0,04 |
|
Раскос под углом 57 градусов 530×12 |
||||||
|
№ 1 |
–254,37 |
0,16 |
–7,33 |
3,98 |
2,98 |
0,40 |
|
№ 2 |
–260,95 |
0,16 |
4,67 |
–0,26 |
0,35 |
0,40 |
|
№ 3 |
–267,27 |
0,16 |
–10,75 |
–4,51 |
–2,27 |
0,40 |
Существуют как минимум три разновидности оценки волнового воздействия на вертикальный элемент. Один из них предполагает рассмотрение этого воздействия в виде равнодействующей сосредоточенной силы. Величина равнодействующей нагрузки на вертикальный элемент диаметром 720 мм при таком подходе может достигать 19 кН. Существует также методика оценки этого воздействия как распределенной нагрузки, приходящейся на единицу длины, в этой ситуации нагрузка будет достигать порядка 1,47 kN/m. Однако, как показал проведенный автором анализ современных теорий волнового воздействия, эти теории не учитывают одну важную особенность волнового воздействия. А именно изменение его величины и направления действия в процессе обтекания конструкции. Различные теории позволяют вычислять значения волновой нагрузки при действии в «лоб», т.е. под углом 0° градусов по отношению к лучу волны, а также значения нагрузки, возникающие за преградой, т.е. под углом 180°. В реальности при обтекании волной периметра вертикальной колонны величина давления при действии давления под углом 90° по отношению к лучу волны ниже в приблизительно в 5 раз по сравнению с величиной давления, действующего в «лоб». Данные выводы подтверждаются расчетом по формуле 17 ВСН 41.88. Проведем моделирование процесса обтекания вертикальной колонны по формуле
![]() (2)
(2)
где p – величина волнового давления, kN/m2; ρ – плотность морской воды, ρ = 1,03 т/м3 или ρ = 1030 кг/м3; g – ускорение свободного падения, g = 9,81 м/с2; h – высота волны, м; ch – гиперболический косинус; d – глубина моря; z – координата, отсчитываемая от уровня моря; χ-коэффициент распределения давления по периметру, определяемы по чертежу 6 ВСН 41.88. Следует отметить, что максимальное давление достигается при положении z = 0, поэтому расчеты будем проводить по наихудшему из возможных вариантов, т.е. предположив что рассматриваемое нами сварное соединение находится на расчетном уровне моря. Момент этой нагрузки рассчитаем в зависимости от величины равнодействующей волновой нагрузки и координаты ее приложения, вычисленной в соответствии с приложением Е.5 СП 38.13330.2012. Произведем расчеты, исходя из анализируемых нами условий, и результаты приведем в табл. 2. Знаки «+» и «–» указывают направление действия волнового давления. Предварительно автором были установлены характеристики волнения в условиях Субботинского месторождения, которые также приведены в табл. 2.
Таблица 2
Результаты расчета действия волновой нагрузки на вертикальную колонну диаметром 720 мм
|
Продолжительность непрерывного волнового воздействия, с |
Параметры волн |
Величина волнового давления на вертикальный элемент, kN/m2 |
Общее количество циклов в год |
Величина условной равнодействующей силы, действующей по направлению движения волны |
Координаты приложения равнодействующей (плечо силы) от уровн моря, m |
Величина момента MP равнодействующей волновой нагрузки, kN∙m |
|||||
|
Коэффициент распределения давления, χ |
|||||||||||
|
0,5 |
0,1 |
-0,3 |
|||||||||
|
Точки периметра опорной стойки в зависимости от угла по направлению к лучу волны |
|||||||||||
|
h |
T |
λ |
0 |
90° |
180° |
0° |
180° |
||||
|
Скорость ветра 10 метров/секунду |
|||||||||||
|
1·104 |
0,82 |
3,87 |
23,4 |
4,14 |
0,83 |
–2,49 |
831·103 |
3,49 |
–3,47 |
3,4 |
±22 |
|
Скорость ветра 15 метров/секунду |
|||||||||||
|
7,56·104 (21 ч) |
2,29 |
6,88 |
73,9 |
11,57 |
2,31 |
–6,94 |
547·103 |
9,84 |
–9,68 |
10,57 |
±104 |
|
Скорость ветра 20 метров/секунду |
|||||||||||
|
6,1·104 |
3,26 |
8,15 |
104 |
16,47 |
3,29 |
–9,88 |
65·103 |
14,1 |
–13,78 |
14,9 |
±211 |
|
Скорость ветра 25 метров/секунду |
|||||||||||
|
4,3·104 |
4,45 |
8,91 |
126 |
22,8 |
4,56 |
–13,49 |
14,9·103 |
19,48 |
–18,81 |
18,04 |
±351 |
При действии волновой нагрузки под углом 0° по отношению к лучу волны сварной шов подвергается действию волнового давления с коэффициентом распределения давления χ = 0,5, в то время как при воздействии под углом 90° по отношению к лучу волны χ = 0,1. Однако возможна ситуация, при которой на сварной шов будет воздействовать «лобовое» давление, например, после прохождения первой стойки такое давление будет воздействовать на следующую за ней. Поэтому расчеты будут проведены по значениям максимально действующего волнового давления, т.е. сварное соединение под углом 0° по отношению к лучу волны. Следует отметить, что максимальные значения коэффициента распределения волнового давления χ находятся в диапазоне от 0° до 45°, после чего они начинают убывать, а вместе с ними и величина волнового давления.
Перейдем к расчету нагрузок на горизонтально расположенный элемент. В рассматриваемом нами случае это элемент диаметром 530 миллиметров и толщиной стенки 12 миллиметров. Он также имеет свою особенность. При приближении к горизонтальному элементу платформы вершины волны нагрузка считается со знаком «+», при удалении от элемента вершины волны нагрузка считается со знаком «-». Расчеты проводились в соответствии с приложением Е. СП 38.13330.2012. Результаты приведены в табл. 3.
Также при воздействии волновой нагрузки на горизонтальный элемент возникает момент этой нагрузки, результаты расчета которого также приведены в табл. 3, с учетом того, что что по данным проекта длина горизонтального элемента l = 14 м.
Перейдем к суммированию напряжений от волновой нагрузки. Совершенно очевидно, что сила давления на вертикальную колонну Р можно рассматривать как силу, действующую в горизонтальной плоскости перпендикулярно вертикальной колоне диаметром 720 мм и параллельной продольной оси горизонтального элемента диаметром 530 мм (рис. 3).
Распределенная нагрузка от волнового воздействия на горизонтальный элемент q будет действовать перпендикулярно к продольной оси горизонтального элемента диаметром 530 мм. Если представить циферблат часов и рассматривать вектор действия силы q, то в точках в направлении на 6 и 12 часов эта сила будет действовать по касательной к горизонтальному элементу и сварному соединению, в точках в направлении на 3 и 9 часов по нормали к нему. В сумме же волновая нагрузка даст вектор, который в виду особенностей геометрии углового сварного шва в точках в направлении на 3 и 9 часов будет направлен перпендикулярно поверхности шва (рис. 3). В точках в направлении на 6 и 12 часов сила q будет создавать касательные напряжения, и, как показали предварительные расчеты, проведенные автором, момент этот силы, который значительно увеличивает величину действующего в сварном соединение напряжения, будет незначительным. Поэтому расчеты будут проводиться для положения 3 и 9 часов. Рассчитаем проекцию суммарной силы от волнового воздействия τ* на горизонтальную ось Y:
![]() (3)
(3)
т.к. моменты, вызванные волновыми нагрузками, также являются величинами векторными, и моменты этих сил МР и Мq действуют в перпендикулярных друг другу плоскостях, то суммарный момент Mτ от действия нагрузки на сварное соединение можно рассчитать согласно теореме Вариньона как
![]() (4)
(4)
таким образом, автором предлагается следующая формула для расчета напряжения, от волнового воздействия τсум:
![]() (5)
(5)
где Мτ – момент силы от действия суммарной нагрузки;а остальные значения такие же, как в формуле (1).
Таблица 3
Волновое давление на горизонтальный элемент.
|
Продолжительность непрерывного волнового воздействия, с |
Параметры волн |
Величина волнового давления на один квадратный метр горизонтального элемента, расположенного параллельно движению волны, принятая по максимальным расчетным значениям, KN/m2 |
Общее количество циклов в год |
Величина момента |
Величина распределенной нагрузки q, kN/m |
||
|
h |
T |
λ |
|||||
|
Скорость ветра10 метров/секунду |
|||||||
|
1·104 |
0,82 |
3,87 |
23,40 |
0,29 |
831·103 |
±12 |
0,49 |
|
Скорость ветра 15 метров/секунду |
|||||||
|
7,56·104 (21 ч) |
2,29 |
6,88 |
73,9 |
0,39 |
547·103 |
±15 |
0,63 |
|
Скорость ветра 20 метров/секунду |
|||||||
|
6,1·104 |
3,26 |
8,15 |
104 |
0,48 |
65·103 |
±20 |
0,82 |
|
Скорость ветра 25 метров/секунду |
|||||||
|
4,3·104 |
4,45 |
8,91 |
126 |
0,74 |
14,9·103 |
±31 |
1,28 |
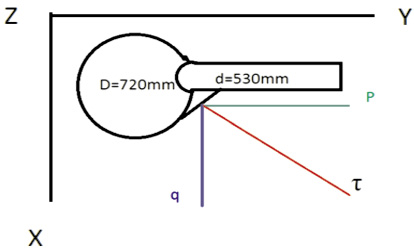
Рис. 3. Схема волнового воздействия на сварное соединение
В результате расчетов установлено, что длина сварного соединения L = 2,28 м. Исходя из простейших геометрических формул, получим, что суммарная площадь поверхности сварного шва S = 0,051 м2. Проведя необходимые расчеты, окончательно получим величины размаха напряжений, возникающих в сварных соединениях при действии волновой нагрузки и стационарных сил. Для удобства дальнейших вычислений переведем значения полученных напряжений в KN/sm2. После чего, исходя из правила суммирования векторов, получим значение полного напряжения, действующего в сварном соединении. Результаты расчета приведены в табл. 4.
Таблица 4
Циклы напряжений в сварном соединении опорного блока МСП
|
Продолжительность непрерывного волнового воздействия, с |
Параметры волн |
Величина напряжений в сварном соединении при действии волновой нагрузки, KN/sm2 |
Размах напряжений в сварном соединении от действия волновой нагрузки и стационарных сил, KN/sm2 |
Общее количество циклов в год |
||
|
h |
T |
λ |
||||
|
Скорость ветра 10 метров/секунду |
||||||
|
1·104 |
0,82 |
3,87 |
23,40 |
±0,23 |
–0,22+0,4 |
831·103 |
|
Скорость ветра 15 метров/секунду |
||||||
|
7,56·104 (21 ч) |
2,29 |
6,88 |
73,9 |
±0,96 |
–0,91+1,1 |
547·103 |
|
Скорость ветра 20 метров/секунду |
||||||
|
6,1·104 |
3,26 |
8,15 |
104 |
±1,85 |
–1,82+1,88 |
65·103 |
|
Скорость ветра 25 метров/секунду |
||||||
|
4,3·104 |
4,45 |
8,91 |
126 |
±3,05 |
–3,03+3,07 |
14,9·103 |
Как показали расчеты, ориентация по отношению 0° и 90° не играет решающей роли в формировании величины напряжений, т.к. основная составляющая напряжений возникает под действием изгибающих моментов. Таким образом в статье описана методика и выполнена в соответствии с разработанной методикой оценка действующих в сварном соединении напряжений, что открывает возможность к экспериментальному определению количества циклов нагрузки до разрушения сварного соединения опорного блока МСП. Результаты эксперимента будут опубликованы позднее.
Рецензенты:Бородавкин П.П., д.т.н., профессор, генеральный директор АО «Интергаз», г. Москва;
Литвин И.Е., д.т.н., генеральный директор ООО «СТД», г. Москва.
Работа поступила в редакцию 05.12.2013.



