Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Сокращение расходов на строительство энергетических систем является важной и актуальной задачей. Так, при проектировании подобных систем необходимо решить ряд важных задач, связанных с минимизацией затрат, а именно минимизацией расходов на строительство, минимизацией длины силового кабеля, минимизацией общей стоимости строительства и т.д.

Решение задач минимизации сводится к задаче структурной оптимизации, которая относится к классу задач дискретной оптимизации и, как следствие, имеет комбинаторный характер, что затрудняет ее решение при больших размерностях.

При анализе различных комбинаций ограничений и реальных ситуаций в энергетических системах был сделан вывод, что поставленная задача структурной оптимизации сводится к задачам размещения и в некоторых случаях к транспортным задачам и задачи коммивояжера. Все эти задачи имеют ярко выраженный комбинаторный характер и являются как минимум NP-трудными в сильном смысле слова.

Алгоритмы муравьиных колоний для решения задач размещения

Основными задачами структурной оптимизации являются задачи размещения с различными ограничениями, решение которых достаточно трудоемко при больших размерностях.

Обозначим через I = (1,...,n) множество конечных потребителей, каждое из которых должно быть подключено только к одному объекту энергораспределения; J = (1,..., m) – множество мест, в которых можно разместить объект энергораспределения; bij ≥ 0, i ∈ I, j ∈ J – стоимость подключения j-го объекта энергораспределения к i-му конечному потребителю. Стоимость прямо пропорциональна стоимости укладки кабеля, стоимости кабеля и расстоянию между объектом и потребителем; qj > 0, j ∈ J – емкость объекта энергораспределения, выраженная в допустимом количестве подключаемых к нему конечных потребителей; cj ≥ 0, j ∈ J – стоимость установки объекта энергораспределения на j-м месте-кандидате; xij ∈ {0, 1} принимает свои значения в зависимости от того, к какому объекту энергораспределения подключен текущий конечный потребитель; yj ∈ {0, 1} принимает значения в зависимости от того, установлен ли объект энергораспределения в текущем месте.

Задача с ограниченным числом подключаемых конечных потребителей. Эта задача формализуется следующим образом:

(1)

(2)

Ограничение (2) означает, что возможное число подключаемых потребителей к объекту энергораспределения не будет превышать заданного значения.

Задача с ограниченным числом объектов энергораспределения. Имея множество мест возможной установки объектов энергораспределения J ∈ {1, ..., m}, из всех возможных множеств, формирующих структуру системы, необходимо выбрать такое множество S ⊆ J, чтобы суммарная функция затрат была минимальной, и все конечные потребители, принадлежащие множеству I ∈ {1, ..., n}, были подключены, но при этом число объектов энергораспределения не должно превышать заданного числа p. Теперь задачу можно сформулировать так:

(3)

< (4)

Для обеих задач выполняется ограничение

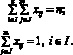(5)

Ограничения (5) гарантируют, что все конечные потребители будут подключены, и один конечный потребитель может быть подключен только к одному объекту энергораспределения.

Для поставленной задачи были разработаны алгоритмы, основанные на классическом алгоритме муравьиной колонии, предложенные М. Дориго [3, 4]. В силу специфики задачи классический алгоритм муравьиных колоний был модифицирован.

На рисунке приведена блок-схема предложенных алгоритмов.

Перечислим основные отличия разработанного алгоритма от классического муравьиного алгоритма:

1. В отличие от классического алгоритма муравьиных колоний в предложенных алгоритмах маршрут не строится постепенно в течение нескольких циклов. Единовременно выбранное муравьем-агентом в течение одного цикла множество объектов энергораспределения и подключенных к ним конечных потребетилей определяют маршрут для задачи с ограниченным числом конечных пользователей. Для задачи же с ограниченным числом объектов энергораспределения маршрутом является множество выбранных объектов энергораспределения.

2. Формула оценки количества феромона имеет вид

(6)

здесь ‒ количество наносимого виртуального феромона на итерации муравья k; Q – регулируемый параметр, значение которого выбирают одного порядка с длиной оптимального маршрута; F – текущее оптимальное решение; Rk – стоимость маршрута, выбранного k-м муравьем-агентом.

В отличие от классического муравьиного алгоритма в (6) введен критерий оценки количества наносимого феромона. Если стоимость маршрута k-го муравья больше текущего значения целевой функции, то количество наносимого феромона равно нулю.

3. Кроме того, иначе определяется сама формула расчета количества наносимого феромона. Отметим, что первоначально, следуя идее классического муравьиного алгоритма, количество наносимого феромона рассчитывалось по формуле

(7)

где есть расстояние между i-м конечным потребителем и j-м объектом энергораспределения. Соблюдая данное условие, алгоритм показывает хорошие результаты в задаче, где стоимость установки объекта энергораспределения не включается. При включении же стоимости целесообразней пользоваться формулой из (6). То есть параметр был заменен на Rk – стоимость маршрута k-го муравья.

4. Для задачи с ограниченным числом объектов энергораспределения формула вероятности выбора мест установки объектов энергораспределения выглядит следующим образом

(8)

тогда как в классическом муравьином алгоритме и в модифицированном алгоритме для задачи с ограниченным числом подключаемых конечных потребителей формула вероятности имеет вид

(9)

где ηij – величина, обратная расстоянию, или так называемая видимость муравья, α и β – два регулируемых параметра, задающие веса следа феромона и видимости при выборе маршрута. Как видим из (8), в формуле вероятности были убраны параметры ηij и β. В самом классическом алгоритме данные параметры играли косвенную роль в минимизации расстояния, и их включение было необходимо. Для данной задачи эти параметры не являются обязательными, также исключение этих параметров позволило сократить время на поиск наилучшего решения при работе алгоритма.

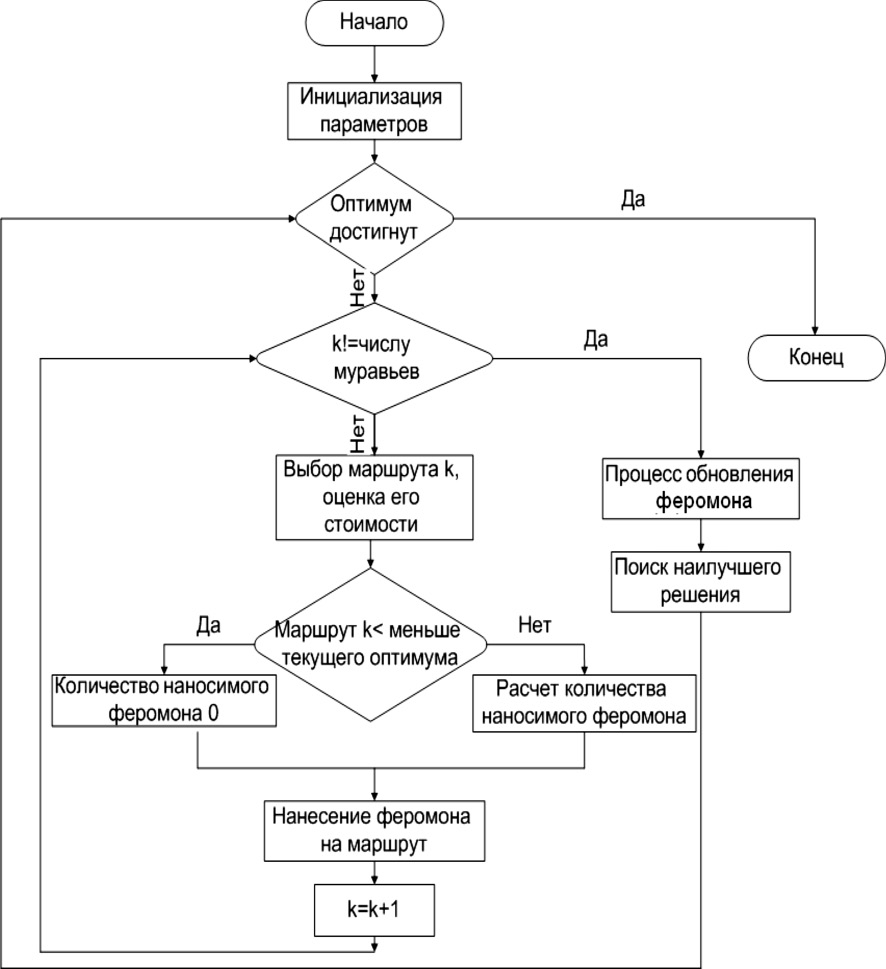
Блок-схема алгоритмов для задач размещения

Такие этапы, как нанесение количества феромона и процедура испарения феромона, остались без изменений. Обозначим коэффициент испарения феромона через ρ ∈ [0, 1]. Тогда правило обновления феромона примет вид

τj = τj(1 – ρ). (10)

Проведение экспериментальных тестирований

Для проведения численных экспериментов и моделирования полученных алгоритмов, в частности, алгоритма муравьиной колонии (ACO) использовалась среда для имитационного моделирования AnyLogic.

Наиболее важными параметрами в алгоритме муравьиной колонии помимо числа муравьев являются параметры α, β, ρ. Параметры α и β отвечают за веса следа феромона, тогда как параметр ρ отвечает за скорость испарения феромона. Выбор ключевых параметров излишне большим или, наоборот, маленьким может привести к слишком быстрому вырождению алгоритма и получению одного субоптимального решения.

Для каждой из поставленных задач помимо муравьиного алгоритма использовался генетический алгоритм(GA). Данный алгоритм, как и многие другие направления и методы искусственного интеллекта, такие как иммунные сети [1], нейросети, алгоритмы имитации отжига уже хорошо зарекомендовали себя при решении подобного рода задач и задач дискретной оптимизации.

Алгоритмы тестировались на матрицах одинаковых размерностей, которые были сгенерированы случайным образом. Координаты точек расположения объектов энергораспределения и конечных потребителей были идентичны для обоих алгоритмов.

Что касается таких параметров, как α, β, ρ, коэффициента мутации, уровня кроссинговера, то для работы алгоритмов мы старались придерживаться единых параметров всегда. Подбор оптимальных значений параметров проводился на различных тестовых задачах с различной размерностью путем увеличения или уменьшения их значений и дальнейшим сравнением результатов работы алгоритмов с заданными параметрами.

При решении задач малой размерности сравнение целевой функции проводилось с решениями, которые были получены методом точного перебора. При увеличении размерности матриц проводить сравнение результатов работы генетического и муравьиного алгоритмов с полным перебором уже не представляется возможным.

В табл. 1–2 приведены результаты работ обоих алгоритмов для обеих задач. Для величин целевых функций приведены наилучшие значения, полученные в течение 100 запусков обоих алгоритмов.

Таблица 1

Таблица 2

Как видим, на матрицах малых размерностей результаты работы обоих алгоритмов идентичны, но с увеличением размерности результаты работы муравьиного алгоритма превосходят генетический алгоритм как в скорости нахождения оптимального решения, так и в значении целевой функции. С увеличением размерности задач муравьиный алгоритм дает на выходе меньшее значение целевой функции, нежели генетический алгоритм.

Заключение

Таким образом, мы показали эффективность работы предложенных модифицированных муравьиных алгоритмов при решении задач структурной оптимизации энергетических сетей. Существенным плюсом подобных алгоритмов является их быстродействие, а также легкость реализации. Но также имеется ряд недостатков, например, таких как подбор параметров. В дальнейшем планируются исследования по нейтрализации этих недостатков и улучшению работы алгоритмов в целом.

Семенов М.Е., д.ф-м.н., профессор кафедры цифровых технологий Воронежского государственного университета, г. Воронеж;

Кургалин С.Д., д.ф-м.н., профессор, заведующий кафедрой цифровых технологий Воронежского государственного университета, г. Воронеж.

Работа поступила в редакцию 05.12.2013.