Одним из фундаментальных вопросов изучения современных движений земной коры (СДЗК) в региональном масштабе на техногенных геодинамических полигонах нефтегазовых месторождений является выбор начала координат (исходного геодезического знака), относительно которого определяются кинематические характеристики эндогенных процессов и техногенных деформаций приповерхностных слоев земной коры. Классически [5, 6] исходный геодезический знак располагают за пределами горного отвода месторождения на расстоянии 2–3 км от его границ. Известно [1, 2], что основным требованием, предъявляемым к исходным геодезическим знакам, является сохранение ими стабильного положения в пространстве и во времени на протяжении выполнения повторных маркшейдерско-геодезических наблюдений. Однако многочисленные исследования [7, 9] в области изучения современных вертикальных движений земной коры (СВДЗК) показывают, что земная поверхность практически повсеместно подвергается сложнодифференцированным в пространстве и во времени смещениям и деформациям, которые являются итогом совместного протекания в ее приповерхностных слоях эндогенных и экзогенных геомеханических процессов [2, 4, 10], что неизбежно приводит к дестабилизации геодезических знаков. Кроме этого, следует обратить внимание на то, что отбор углеводородов на разрабатываемых месторождениях приводит к перетоку подземных вод из приповерхностных слоев земной коры, удаленных более чем на 2–3 км от границ горного отвода, которые вследствие изменения уровня подземных вод претерпевают деформации [10]. Следовательно, традиционный подход [5, 6] к выбору начала координат на техногенных геодинамических полигонах исключает возможность строгого решения задачи определения кинематических характеристик техногенных деформаций приповерхностных слоев земной коры и границ их проявления на земной поверхности.
Программно-целевой подход к изучению СДЗК и ее приповерхностных слоев на территориях нефтегазовых месторождений [3] предусматривает на контрольных кустах реперов наблюдательных систем геодинамических полигонов использование в качестве исходных геодезических знаков глубинные реперы (разведочные скважины, оборудованные под реперы), основания которых заложены в горные породы, расположенные ниже коллекторов, из которых производится отбор углеводородов. Таким образом, на месторождении имеется сеть исходных геодезических знаков, на устойчивость которых не влияют экзогенные природные и антропогенные факторы, однако их устойчивость нарушается под воздействием тектонических факторов. Поэтому нами предлагается на первом этапе обработки результатов повторных геодезических наблюдений оценить устойчивость глубинных (исходных) реперов по отношению к эндогенным факторам и определить скорости СВДЗК в пределах геодинамического полигона, которые в дальнейшем будут использоваться для вычисления кинематических характеристик техногенных деформаций приповерхностных слоев земной коры и ее поверхности с учетом тектонической составляющей дестабилизации опорного геодезического знака, выбранного в качестве исходного.
Для этого при обработке результатов повторных геодезических наблюдений, в частности, повторного нивелирования, принимая поочередно за исходный все опорные i-е реперы геодинамического полигона вычисляют отметки j-х остальных, после сопоставления которых в двух циклах повторных измерений получают n рядов расхождений отметок Δij (i = 1,…n; j = 1…n). Полученные расхождения сводят в квадратную матрицу:

Сумму столбцов Sj матрицы Bn делят на n и получают средние смещения j-х реперов относительно всех остальных нивелирных знаков за период времени τ между циклами повторных наблюдений, обусловленных тектоническими факторами. Средняя «точечная» скорость вертикальных движений земной коры на участке между j и j + 1 знаками может быть получена из выражения
![]() (1)
(1)
Скорости СВДЗК для районов закладки опорных геодезических знаков также можно определить по картам СВДЗК [9], которые составлены для европейской территории России.
Для определения скоростей СВДЗК на заданный район по картам СВДЗК выполняется интерполирование скоростей, представленных на картах СВДЗК изолиниями, и оценка погрешности площадного интерполирования по точечным значениям скоростей.
При интерполировании скоростей СВДЗК по площади P задаются структурой СВДЗК и точностью получения скоростей СВДЗК, сведения о которой представлены на картах СВДЗК. Интерполяционные веса определяются на основании сведений о статистической структуре СВДЗК и точности получения скоростей СВДЗК таким образом, чтобы средняя квадратическая погрешность нивелирования была минимальной по сравнению с ее значениями при любом другом выборе весов.
Принимая гипотезу с нулевым значением скорости СВДЗК в n = 1…i точках (xi, yi), считаем вычисленные по результатам повторного нивелирования скорости СВДЗК Vi отклонениями от истинных значений. Тогда справедливо следующее уравнение:
![]() (2)
(2)
или в линейном виде
![]() (3)
(3)
где ai – веса, определяемые из условия, чтобы средний квадрат погрешности замены величины (2) величиной (3) с учетом ошибок нивелирования δi был минимальным:
![]() (4)
(4)
В формуле (4) черта сверху указывает на осреднение, осуществляемое, строго говоря, в вероятном смысле, но на некоторой ограниченной выборке.
Используя структурную функцию и принимая во внимание свойства случайных ошибок:
а) ошибки δv в различных точках не коррелированы ни с истинными значениями величин скоростей
δv (x1, y1) v (x2, y2) = 0; (5)
б) ни между собой
![]() , (6)
, (6)
где ![]() – средняя квадратическая погрешность определения скорости СВДЗК; d12 – расстояние между точками 1 и 2.
– средняя квадратическая погрешность определения скорости СВДЗК; d12 – расстояние между точками 1 и 2.
Определяем случайную ошибку измерения скоростей СВДЗК методами повторных геодезических наблюдений. Такое обобщение допустимо, поскольку мы имеем уравненные значения скоростей СВДЗК, представленных на картах СВДЗК.
Представим значения скоростей в точках (x1, y1) для конкретного региона в виде последовательного ряда измерений. Принимая наряду с однородностью и изотропией СВДЗК для платформенного района, что не противоречит природе нетектонических движений земной коры, условие зависимости mv от координат, можем определить значения mv в каждой из точек (x1, y1). Структурная функция скоростей v по двум последовательно расположенным точкам в ряде измерений представляют собой средний квадрат разности
![]() (7)
(7)
Структурная функция Sv завышена на сумму средних квадратов ошибок в точках. Это верно для всех расстояний d, кроме d = 0, при котором функция Sv = 0.
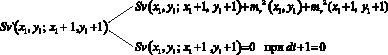
Принимая во внимание данное свойство структурной функции, экстраполируя функцию Sv`к di + 1, получаем ![]() .
.
Определение ковариационной функции и свойства (5) и (6) позволяют записать
![]() (8)
(8)
Приняв обозначения:
Ковариационная функция
tv(xi, yi, xj, yj) = tij
![]()
и дисперсия среднего значения скоростей СВДЗК по площади P через
![]()
перепишем уравнение (8)
![]() (9)
(9)
где ki – значение взаимной ковариационной функции, описывающей статистическую связь точечных значений с осредненной по площади величиной.
Веса ai определяются из условий минимума М. Для этого приравниваются производные от М по весам ai к нулю. Получается система n линейных уравнений
![]() (i = 1…n), (10)
(i = 1…n), (10)
где ![]() (11)
(11)
Согласно изложенному выше,
![]() (12)
(12)
![]() (13)
(13)
Принимая однородность и изотропность для ковариационной функции и разбивая район на прямоугольники (квадраты) в формулах (2), (12) и (13) без труда вычисляется интеграл при определении величин Vср, Е и ki с использованием линейных алгебраических уравнений (3), (9) и (10). При этом следует иметь в виду, что отношение k/t = R представляет собой коэффициент корреляции, характеризующий связь между значениями Vср скоростей СВДЗК. По коэффициентам корреляции R можно судить о региональном поднятии (опускании) групп реперов. Следовательно, данная методика обработки результатов повторного нивелирования также может успешно применяться для анализа устойчивости реперов исходной основы в условиях воздействия на них как эндогенных, так и экзогенных геоме ханических процессов.



