Решение даже небольших на первый взгляд задач в экономике связано с выполнением множества расчетов, применением различных методов обработки информации, разработкой различных вариантов решений и обоснованием среди них выбираемых для реализации. Поэтому не вызывает сомнения актуальность разработки компьютерных моделей для автоматизации расчетов и процедур обработки информации, реализующих различные методы и математические инструментарии.
Целью настоящего исследования является разработка компьютерной модели и методики для оценки тенденций и зависимостей в экономике регионов, основывающиеся на построении различными методами моделей с распределенным лагом времени и авторегрессии. В качестве объекта, по данным которого разработана методика, выбраны регионы Северокавказского федерального округа, а в качестве предмета – величины двух ключевых показателя (валового регионального продукта и инвестиций) за 2002–2010 гг. [6].
Особенностью инвестиций является то, что от их объема за тот или иной период времени зависит ВРП не только за этот период, но и за несколько последующих периодов. Особенность ВРП состоит в том, что его величина за t-й год зависит не только от объема инвестиций за этот же период, но и от величин ВРП за (t – 1)-й, (t – 2)-й…(t – l)-й годы.
То есть искомые динамические зависимости можно записать в виде функций:
yt = f(xt, xt–1, xt–2, …, xt–l); (1)
yt = f(xt, yt–1, yt–2, …, yt–l), (2)
где yt, xt – величины ВРП и инвестиций за t-й год; xt–1, xt–2, …, xt–l; yt–1, yt–2, …, yt–l – объемы соответственно инвестиций и ВРП за (t – 1)-й, (t – 2)-й,… (t – l)-й годы.
Зависимости могут быть линейными и нелинейными. В случае линейной зависимости функции (1 и 2) примут вид:
yt = b + m0xt + m1 xt–1 + m2xt–2 + ⋯ +mlxt–l, (3)
yt = b + m0xt + m1yt–1 + m2yt–2 + ⋯ + mlyt–l. (4)
Модели вида (1) и (3) называются моделями с распределенным лагом времени, а вида (2) и (4) – моделями авторегрессии [3, 5, 7].
Для каждого региона при одних и тех же исходных данных можно строить модели с различными лагами. Максимальный лаг должен быть, с нашей точки зрения, меньше или равен одной трети длины рассматриваемого периода. В нашем случае длина периода составляет 10 лет (2002–2011 гг.). Поэтому лаг времени принят равным 1, 2 и 3. Возможны разные вариации моделей с распределенным лагом времени и авторегрессии с различным числом переменных (в нашем случае – с одним, двумя, тремя лаговыми переменными).
Поскольку расчеты требуется проводить для любого региона (федерального округа, страны в целом, для групп регионов) нами разработана компьютерная модель, автоматизирующую все вычисления и формирующая исходные, промежуточные и аналитические таблицы. Она включает в себя базу данных социально-экономических показателей регионов РФ, совокупность таблиц-шаблонов (для исходных, промежуточных и аналитических данных), встроенные статистические функции MS Excel, а также совокупность введенных в таблицы-шаблоны формул, обеспечивающих выполнение всех расчетов и процедур обработки информации. Ее условно можно разбить на три модуля: 1-й – для построения моделей с распределенным лагом; 2-й – для построения моделей авторегрессии; 3-й – для формирования расчетно-аналитических таблиц параметров и характеристик группы регионов (в нашем случае регионов СКФО).
Первый модуль предусматривает построение 15-ти моделей с распределенным лагом с различным числом лаговых переменных: 4-х с одним переменным, 6-ти – с двумя, 4-х – с тремя и одного – с четырьмя переменными. Исходные данные, необходимые для построения всех 15-ти моделей организованы в виде двух таблиц-шаблонов. Для размещения результатов расчетов созданы 15 промежуточных таблиц-шаблонов, сгруппированных в четыре группы соответственно для моделей с 1-м, 2-мя, 3-мя и 4-мя переменными. Аналитические таблицы-шаблоны (соответственно для моделей с 1-м, 2-мя, 3-мя и 4-мя переменными) – это таблицы, в которые из промежуточных таблиц-шаблонов переведены величины параметров моделей (свободные члены и коэффициенты при переменных), а также группы статистических характеристик, предназначенных для оценки приемлемости построенных моделей.
С точки зрения анализа особый интерес представляют коэффициенты при переменных моделей. Поэтому создана 5-я аналитическая таблица-шаблон для этих коэффициентов, фрагмент которой приведен в табл/ 1.
Модели с двумя, тремя и четырьмя переменными можно строить по принятой в литературе методике и/или по методике, предлагаемой нами.
Сущность предлагаемой нами методики состоит в построении моделей с двумя, тремя и четырьмя переменными на основе 4-х моделей с одной переменной. При этом параметры и характеристики четырех моделей с одной переменной определяются методом наименьших квадратов. Для построения остальных моделей достаточно сложить левые и правые части моделей с одной переменной в различных комбинациях и обе части полученных сумм разделить на число, равное количеству складываемых уравнений. Так, если сложить 1-ю и 2-ю модели, построенные для РД, и разделить обе части после суммирования на два, то получится модель с распределенным лагом, содержащая две переменные:
Yt = 29,109 + 0,9675Xt + 1,082Xt–1. (5)
Аналогично, если сложить левые и правые части всех четырех моделей с одной переменной и разделить обе части суммы на четыре, то можно получить модель с 4-мя переменными:
Yt = 35,301 + 0,4837Xt + 0,5410Xt–1 + 0,5976Xt–2 + 0,6712Хt–3. (6)
Сравнение параметров моделей (5) и (6) по обеим методикам дают весьма схожие результаты. В частности, ∑ml при обеих методиках оказались примерно равными: 2, 13; 2,09 – по 1-й методике; 2,05; 2,29 – по 2-й методике.
Для построения всех 11-ти моделей с двумя, тремя и четырьмя переменными по предлагаемой нами методике требуется создать еще три таблицы-шаблоны соответственно, в ячейки которых вводятся формулы, реализующие предлагаемую методику.
Методика построения моделей авторегрессии (модуль 2) отличается от методики построения моделей с распределенным лагом. Отличие состоит в методике расчета параметров. В соответствии с [3, 5, 7] методика расчета параметров моделей авторегрессии (см. формулу (4)) состоит из двух процедур:
а) методом наименьших квадратов рассчитываются параметры и характеристики модели авторегрессии с двумя переменными вида
Yt = b + m0Xt + c1Yt–1; (7)
б) по ее параметрам m0 и c1 определяются параметры при других переменных модели авторегрессии, которая в общем случае имеет вид:
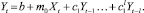 (8)
(8)
Таблица 1
Величины параметров моделей с распределенным лагом при различном сочетании переменных, построенных по данным РД за 2002-2011 гг.
|
Номера уравнения |
Своб. член |
Xt |
Xt–1 |
Xt–2 |
Xt–3 |
|
b |
m |
m1 |
m2 |
m3 |
|
|
1 |
20,973 |
1,9349 |
|||
|
2 |
37,244 |
2,164 |
|||
|
… |
… |
… |
… |
… |
… |
|
5 |
33,988 |
0,3501 |
1,7787 |
||
|
… |
… |
… |
… |
… |
… |
|
11 |
40,057 |
0,5965 |
0,5947 |
1,0224 |
|
|
… |
… |
… |
… |
… |
… |
|
15 |
46,304 |
0,3129 |
0,6431 |
1,7693 |
‒0,630 |
Рассмотренная методика не позволяет, на наш взгляд, в полной мере реализовать возможности моделей авторегрессии. Поэтому нами предлагается включить в эту методику три авторских метода построения моделей авторегрессии: метод достраивания моделей с двумя переменными до моделей с 3-мя и 4-мя переменными; метод построения моделей с 3-мя и 4-мя переменными на основе суммирования моделей с двумя переменными; метод построения моделей с 2-мя, 3-мя и 4-мя переменными на основе суммирования моделей с одной переменной и их последующего достраивания.
При первом методе строятся следующие три модели авторегрессии с 2-мя переменными с лагами 1, 2 и 3 соответственно:
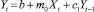 – лаг = 1; (9)
– лаг = 1; (9)
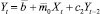 – лаг = 2; (10)
– лаг = 2; (10)
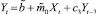 – лаг = 3. (11)
– лаг = 3. (11)
Свободные члены и коэффициенты при переменных этих моделей рассчитываются методом наименьших квадратов [3, 7]. На их основе можно тремя способами построить следующие модели с лаговыми переменными:
– по формуле (7), используя равенства с1 = с1, 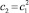 ,
, 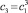 :
:
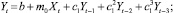 (12)
(12)
– по формуле (9) и равенствам 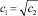 , с2 = с2,
, с2 = с2, 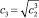 :
:
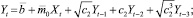 (13)
(13)
– по формуле (11) и равенствам 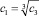 ,
, 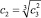 ; с3 = с3:
; с3 = с3:
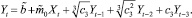 (14)
(14)
Каждая из формул (12), (13) и (14) предполагает возможность построения моделей с двумя, тремя и 4-мя переменными с лагами 1, 2 и 3.
При втором методе также строятся те же три модели авторегрессии (см. (7), (9), (10) выше) с 2-мя переменными с лагами 1, 2 и 3 соответственно. Путем суммирования моделей (а) и (б) и деления обеих частей сумм на число два можно построить модель с тремя переменными, а путем суммирования моделей (7), (9), (10) и деления обеих частей сумм на число три – модель с 4-мя переменными, которые имеют вид:
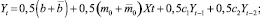 (15)
(15)
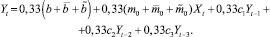 (16)
(16)
Третий метод состоит в следующем:
– методом наименьших квадратов определяются свободные члены и коэффициенты при переменных (коэффициентов регрессии) для четырех следующих моделей с одной лаговой переменной (лагом 0, 1, 2 и 3):
Yt = b0 + m0Xt; (17)
Yt = b1 + c1Yt–1; (18)
Yt = b2 + c2Xt–2; (19)
Yt = b3 + c3Xt–3; (20)
– просуммировав модели (17) и (18); (17), (18) и (19); (17), (18), (19) и (20) и разделив первую сумму на 2, вторую – на 3 и третью – на 4, можно получить следующие модели:
Yt = 0,5∙(b0 + b1) + 0,5∙m0Xt + 0,5∙c1Yt–1; (21)
Yt = 0,33∙(b0 + b1 + b2) + 0,33m0Xt + 0,33c1Yt–1 + 0,33c2Yt–2; (22)
Yt = 0,25∙(b0 + b1 + b2 + b3) + 0,25m0Xt + 0,25c1Yt–1 + 0,25c2Yt–2 + 0,25c3Yt–3; (23)
– сложив обе части модели (17) поочередно с обеими частями моделей (18), (19) и (20), разделив результаты на 2, а затем, достроив их, можно получить еще три модели авторегрессии:
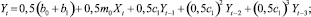 (24)
(24)
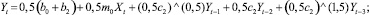 (25)
(25)
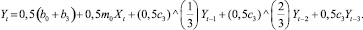 (26)
(26)
Сущность методики построения моделей (7), (9), (10) –(26) состоит в следующем:
– созданы две исходные таблицы-шаблоны для построения четырех моделей с одной переменной и трех моделей с двумя переменными, а также семь промежуточных таблиц-шаблонов для размещения расчетных значений параметров и характеристик моделей с одной и двумя переменными (расчеты выполнены с помощью функции «линейн» из MS Excel);
– созданы аналитические таблицы-шаблоны: две – для параметров и характеристик моделей с одной и двумя переменными, четыре – для коэффициентов при переменных моделей (11)–(14), (15)–(16), (21)–(23), (24)–(26).
В качестве примера в табл. 2 приведены величины коэффициентов при переменных моделей авторегрессии, рассчитанных методом достраивания моделей с 2-мя переменными до моделей с 3-мя и 4-мя переменными по данным РД за 2002–2011 гг.
Как видно из табл. 2, одну и ту же зависимость ВРП (Yt) от объема инвестиций (Xt) и лаговых переменных по ВРП (Yt–1, Yt–2 и Yt–3) можно выразить тремя моделями. Разница числовых значений обусловлена инфляционной составляющей и разницей цен, поскольку ВРП и инвестиции приведены в текущих ценах соответствующих лет.
Для сравнительной оценки параметров и характеристик построенных моделей аналитические таблицы (при необходимости и исходные, и промежуточные) целесообразно транспортировать (скопировать) в MS Word.
Для выполнения расчетов по другим регионам для каждого из них создается копия компьютерной модели. В таблицы-шаблоны с исходными данными созданной копии вместо данных Республики Дагестан, на примере которой она разработана, вводятся данные региона, для которого создана копия. При этом во всех промежуточных и аналитических таблицах-шаблонах автоматически осуществляется перерасчет значений параметров и статистических характеристик.
Поскольку построение некоторых из таблиц предполагает выполнение расчетов, то для их автоматизации нами создан третий модуль компьютерной модели, предусматривающий построение следующих таблиц-шаблонов:
а) для моделей с распределенным лагом:
– четырех аналитических таблиц коэффициентов (b, m0, m1, m2, m3) при переменных Xt, Xt–1, Xt–2, Xt–3 в разрезе регионов СКФО;
– четырех таблиц-шаблонов соотношений коэффициентов при переменных моделей регионов к их величинам по СКФО в целом (относительные коэффициенты определяются путем деления коэффициентов регрессии при переменных моделей регионов на коэффициенты регрессии моделей для СКФО); данные этих таблиц рассчитываются на основе данных предыдущих таблиц;
– двух таблиц-шаблонов с величинами мультипликаторов (краткосрочных, промежуточных и долгосрочных), рассчитываемых на основе коэффициентов m0, m1, m2, m3 полученных по первой и второй методикам;
– двух таблиц-шаблонов с величинами долгосрочных мультипликаторов с лагами времени, равными 1, 2 и 3, полученными по рассмотренным методикам;
б) для моделей авторегрессии:
– трех аналитических таблиц коэффициентов при переменных, полученных по каждому из методов соответственно;
– трех расчетно-аналитических таблиц-шаблонов для мультипликаторов.
Таблица 2
Величины коэффициентов при переменных моделей авторегрессии, рассчитанных методом достраивания моделей с двумя переменными до моделей с 3-мя и 4-мя переменными по данным РД за 2002–2011 гг.
|
Уравнения |
bi |
mi |
с1 |
с2 |
с3 |
|
1. Yt = b1 + m1Xt + c1Yt–1 |
16,733 |
1,033 |
0,531 |
с12 |
с13 |
|
2. Yt = b2 + m2Xt + c2Yt–2 |
19,619 |
1,160 |
с2^(1/2) |
0,568 |
с2^(3/2) |
|
3. Yt = b3 + m3Xt + c3Yt–3 |
18,279 |
1,415 |
с3^(1/3) |
с3^(2/3) |
0,5123 |
|
4. Yt = b1 + m1Xt + c1Yt–1 + c12Yt–2 + c13Yt–3 |
16,733 |
1,033 |
0,531 |
0,282 |
0,149 |
|
5. Yt = b2 + m2Xt + с2^(1/2)Yt–1 + c2Yt–2 + с2^(3/2)Yt–3 |
19,619 |
1,160 |
0,754 |
0,568 |
0,428 |
|
6. Yt = b3 + m3Xt + с3^(1/3)Yt–1 + с3^(2/3)Yt–2 + c3Yt–3 |
18,279 |
1,415 |
0,800 |
0,640 |
0,512 |
Примечание. Численные значение, выделенные жирным шрифтом, рассчитаны методом достраивания, остальные – методом наименьших квадратов.
Одним из важных назначений моделей с распределенным лагом времени и авторегрессии является расчет на основе коэффициентов при их переменных мультипликаторов.
Коэффициент m0 в обоих видах моделей характеризует среднее абсолютное изменение Yt при изменении Xt на единицу в момент времени t, без учета воздействия лаговых значений фактора Xt–1, Xt–2, Xt–3. Этот коэффициент называют краткосрочным мультипликатором.
Сущность методики расчета промежуточных и долгосрочных мультипликаторов для двух видов моделей отлична.
В случае моделей с распределенным лагом при лаге времени l = 1 увеличение каждого из двух факторов Xt, Xt–1 на единицу приводит к изменению результата Yt на величину, равную сумме (m0 + m1), при лаге l = 2 – сумме (m0 + m1 + m2) и т.д. Полученные таким образом величины принято называть промежуточными мультипликаторами. Величину m = m0 + m1 + m2 + … + ml называют долгосрочным мультипликатором. Он показывает абсолютное изменение результата Yt при увеличении на единицу факторов Xt, Xt–1, Xt–2, Xt–3.
Проанализировать и привести всю совокупность полученных нами результатов в рамках ограниченного объема одной статьи не представляется возможным. Поэтому приведем лишь две таблицы, характеризующие величины мультипликаторов по регионам СКФО – по одной для обоих видов моделей с лаговыми переменными. В табл. 3 приведены величины мультипликаторов (краткосрочных, промежуточных и долгосрочных), рассчитанных на основе коэффициентов при переменных моделей с распределенным лагом.
Как показывает анализ, сложилась вполне четкая картина эффективности использования инвестиций по регионам СКФО. В частности по всем долгосрочным мультипликаторам, рассчитанным разными методами, регионы расположились в одной и той же последовательности при всех трех величинах лага времени: Кабардино-Балкарская республика, Республика Северная-Осетия – Алания, Карачаево-Черкесская республика, Ставропольский край, Республика Ингушетия и Республика Дагестан (Чеченская республика не рассматривалась из-за отсутствия данных с 2002 по 2009 гг.).
В модели авторегрессии промежуточные мультипликаторы рассчитываются по формулам: m1 = m0*c1; m1 = m0*c1; 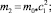 …
… 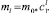 А долгосрочный – по формуле:
А долгосрочный – по формуле:
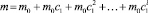
или
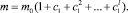
Таблица 3
Величины мультипликаторов (краткосрочных, промежуточных и долгосрочных), рассчитанных на основе параметров моделей с распределенным лагом для регионов СКФО (по первой методике)
|
m0 |
m1 |
m2 |
m3 |
Промеж. мультип. |
Долгоср. мультип. |
||
|
Xt |
Xt–1 |
Xt–2 |
Xt–3 |
m0 + m1 |
m0 + m1 + m2 |
||
|
РД |
0,313 |
0,643 |
1,769 |
–0,630 |
0,956 |
2,725 |
2,095 |
|
РИ |
0,181 |
0,668 |
1,800 |
–0,232 |
0,848 |
2,648 |
2,416 |
|
КБР |
0,791 |
1,242 |
0,762 |
1,643 |
2,033 |
2,795 |
4,438 |
|
КЧР |
0,281 |
0,362 |
0,653 |
2,053 |
0,642 |
1,295 |
3,348 |
|
РСО-А |
1,242 |
1,291 |
–0,617 |
1,733 |
2,532 |
1,916 |
3,649 |
|
Ставр. |
–1,429 |
5,582 |
–2,250 |
1,040 |
4,153 |
1,904 |
2,944 |
|
СКФО |
0,840 |
1,299 |
0,312 |
0,009 |
2,139 |
2,451 |
2,461 |
В табл. 4 приведены величины мультипликаторов, рассчитанных по коэффициентам моделей авторегрессии с 2-мя переменными для регионов СКФО по данным за 2002–2011 гг.
Таблица 4
Величины мультипликаторов, рассчитанных по коэффициентам при переменных моделей авторегрессии по данным регионов СКФО за 2002–2011 гг.
|
m0 |
m0c1 |
m0c12 |
m0c13 |
Мультипликаторы |
|||
|
лаг = 1 |
лаг = 2 |
лаг = 3 |
|||||
|
РД |
0,967 |
0,797 |
0,657 |
0,542 |
1,764 |
2,420 |
2,962 |
|
РИ |
1,049 |
0,759 |
0,551 |
0,399 |
1,808 |
2,359 |
2,758 |
|
КБР |
1,794 |
1,451 |
1,173 |
0,949 |
3,245 |
4,419 |
5,368 |
|
КЧР |
1,421 |
1,098 |
0,850 |
0,657 |
2,519 |
3,369 |
4,026 |
|
РСО-А |
1,554 |
1,170 |
0,883 |
0,665 |
2,724 |
3,607 |
4,272 |
|
Ставр.кр. |
1,364 |
0,997 |
0,730 |
0,533 |
2,361 |
3,091 |
3,624 |
|
СКФО |
1,155 |
0,894 |
0,693 |
0,536 |
2,049 |
2,742 |
3,278 |
Анализ величин мультипликаторов, полученных на основе разных моделей авторегрессии, позволяет сформулировать два важных вывода:
а) с увеличением лага времени долгосрочные мультипликаторы растут по данным всех регионов;
б) по величинам мультипликаторов, рассчитанным на основе моделей авторегрессии, регионы расположились в той же последовательности, что и по моделям с распределенным лагом. Исключением оказалась Республика Дагестан, которая по величинам мультипликаторов при лаге 2 и 3 опережает Республику Ингушетию. Эффективность использования инвестиций по Кабардино-Балкарской республике, являющейся лидером среди регионов СКФО, почти в 2 раза выше, чем по Республике Дагестан.
Рецензенты:Алиев М.А., д.э.н., профессор кафедры экономической теории, ФГБОУ ВПО Дагестанский государственный педагогический университет, г. Махачкала;
Шейхов М.А., д.э.н., профессор, ФГБОУ ВПО Дагестанской государственной академии им. М.М. Джанбулатова, г. Махачкала.
Работа поступила в редакцию 29.11.2013.



