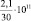Ударное взаимодействие падающих частей ковочного молота с заготовкой сопровождается отскоком. Процесс является прерывистым и существенно нелинейным [2]. Учитывая разницу в возникающих динамических деформациях, при которых пластические деформации заготовки при ударе оказываются весьма значительными (несколько миллиметров), а деформации упругих частей составляют порядка одного миллиметра, представим процесс взаимодействия падающих частей с заготовкой как систему с одной степенью свободы. Эти результаты были получены по методу конечных элементов [1, 2].
Рассмотрим аналитическое описание этого взаимодействия, которое может быть найдено из энергетических соображений.
Пусть изменение потенциальной энергии бабы между двумя соседними отскоками равно:
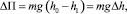
где m – масса падающих частей; g ‒ ускорение свободного падения; h0 – высота падения; h1 – высота подъема при отскоке, Dh – разница высот.
Характер процесса представлен на рис. 1.
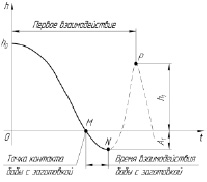
Рис. 1. Процесс взаимодействия падающих частей ковочного молота с заготовкой: h0 ‒ высота падения; h1 ‒ высота подъема при отскоке; А1 ‒ амплитуда сжатия падающих частей; t ‒ время
Для получения аналитического решения рассматриваемой задачи необходимо исключить зависимость, связанную с определением величины h. Зная скорость соударения верхнего бойка с заготовкой, можно определить начальную высоту h из соотношения
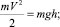
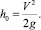
Величину V скорость соударения падающих частей молота с заготовкой можно определить экспериментально.
Упростим процесс до одного взаимодействия падающих частей с заготовкой, это позволит учитывать только одну амплитуду сжатия, при этом изменением высоты падения за счет деформации заготовки пренебрегаем. Поскольку движение падающих частей молота осуществляется за счет паровоздушного устройства молота, то каждый ее удар по заготовке будем рассматривать с новыми начальными условиями (скорость падающих частей, характеристики заготовки). Такой подход позволяет определить амплитуду деформаций заготовки.
Оценим пластические деформации заготовки.
Полагая внутреннее трение в штоке, бабе и верхнем бойке малым и пропорциональным амплитуде сжатия А (это предположение дает хорошее приближение к опыту), сила сопротивления Fv будет
Fv =c0A,
где с0 ‒ коэффициент сопротивления.
Считаем силу взаимодействия между падающими частями и заготовкой постоянной и за время взаимодействия изменение энергии будет
ΔE = с0A2.
Пренебрегая трением о воздушную среду, приравнивая убыль потенциальной энергии ΔП величине рассеяния энергии в материале бабы ΔE, получаем
с0A2 = mgΔh.
При гистерезисном рассеянии энергии, если демпфирование мало, то решение уравнения свободных колебаний может быть получено методом энергетического баланса, согласно которому приравнивается работа сил сопротивления изменению потенциальной энергии системы за один период колебаний. Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией. Поэтому потенциальная энергия, накапливаемая в материале бабы, изменится на величину:
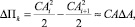
где С ‒ жесткость бабы; ΔA = Ai Ai+1, A = Ai.
Составим дифференциальное уравнение изменения высоты отскоков бабы. Пусть
.
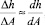При этом
ΔП ≈ CAΔA = mgΔh.
Тогда
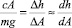и 
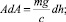
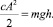
Приближенно положим:
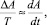
откуда
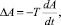
и, следовательно
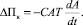
Таким образом,
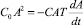
или
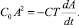
Подставляя
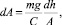
получаем
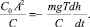
Убыль потенциальной энергии определяется через величину Δh, которая выражается через скорость соударения падающих частей с заготовкой. Обе эти величины взаимосвязаны и могут быть определены экспериментально.
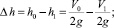
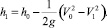
Кривую на рис. 1, отражающую характер изменения высоты падающих частей в процессе работы ковочного молота, можно условно разделить на три участка: 1 до момента соударения верхнего бойка с заготовкой (точка контакта M), 2 участок MN взаимодействия верхнего бойка с заготовкой, при котором происходит операция осадки, 3 участок NP отскока падающих частей. На этом участке коэффициент внутреннего рассеяния энергии γ будем считать равным нулю, пренебрегая внутреннем и внешним рассеянием энергии. После контакта в период взаимодействия верхнего бойка с заготовкой происходит сжатие заготовки с последующим образованием пластических деформаций в заготовке и упругих деформаций в штоке, бабе и верхнем бойке.
Во время предыдущего периода баба накапливает потенциальную энергию взаимодействия, которая за счет восстановления ее упругих деформаций на 3 участке кривой приводит к ее росту.
После отскока падающих частей, который происходит вследствие работы сил сопротивления и энергии деформации заготовки, предположим, что ее высота изменяется по закону затухающих колебаний, при этом уже γ = 0. Это допущение принято для упрощения рассматриваемой задачи и предполагает не учета влияния паровоздушного механизма молота.
Затухающие колебания при наличии силы сопротивления среды, пропорциональной скорости, и описываются следующей формулой [4, 5]:
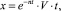(1)
где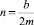 
‒ приведенный коэффициент сопротивления среды,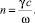 
Это решение дифференциального уравнения колебаний получается при n = k, где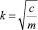 
‒ частота свободных незатухающих колебаний; c ‒ жесткость, c = EF; Е ‒ модуль упругости заготовки; F ‒ площадь поперечного сечения заготовки; 
‒ частота свободных колебаний с учетом затухания;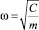 
– частота колебаний.
Получение теоретического закона изменения высоты отскоков падающих частей при ковке имеет практическую значимость при определении осадки заготовки при последующих ударах, когда, рассматривая задачу с новыми начальными условиями при каждом последующем ударе, можно в некоторой степени формализовать процесс ковки, имеющий в настоящее время эмпирический характер.
В качестве примера рассмотрим соударение падающих частей ковочного молота модели М1345 с заготовками, представленными в табл. 1. Испытания проводились в производственных условиях ЗАО «Авиастар-СП» на операциях свободной ковки с целью исследования осадки заготовки в процессе ударного взаимодействия с падающими частями ковочного молота при фиксированном ходе бабы.
Таблица 1
Результаты экспериментальных исследований
|
№ п/п |
Материал заготовки |
Температура ковки, °С |
Форма и размеры заготовки |
Ход бабы, мм |
Размеры заготовки после 1 удара |
Осадка заготовки, мм |
|
1 |
30ХГСА |
1170 |
∅ 45×115 |
635 |
∅ 50×93 |
22 |
|
2 |
30 ХГСА |
1170 |
∅ 45×80 |
670 |
∅ 50×65 |
15 |
|
3 |
12Х18Н10Т |
1170 |
∅ 210×92 |
448 |
∅ 220×83 |
9 |
|
4 |
АК6 |
450 |
110×140×86 |
610 |
95×145×96 |
15 |
Построим кривую (рис. 1), заданную уравнением (1), при следующих исходных данных (табл. 2), взятых для ковочного молота модели М1345 и заготовки № 1 из табл. 1.
Таблица 2
Исходные данные для расчетов [4]
|
Е , Па |
ρ, кг/м3 |
F, м2 |
V, м/с |
g |
|
|
7620 |
0,0016 |
7 |
0,03 |
В результате численных расчетов, осуществленных с помощью программного комплекса MathCAD2001, получен график движения падающих частей ковочного молота в процессе ударного взаимодействия с заготовкой (сплошная линия на рис. 2). Получено, что осадка заготовки после первого удара составляет 21,6 мм, что составляет 2 % расхождение с экспериментальным значением в 22 мм, полученным в результате нахождения разности между высотой заготовки до и после удара (осадки). Полученное расчетное время деформации заготовки 0,01 с.
Сплошная линия на рис. 2 характеризует процесс взаимодействия падающих частей ковочного молота с заготовкой с момента соударения до момента отскока, с которого кривая показана пунктирной линией, потому что реальный закон движения падающих частей на этом участке уже не будет соответствовать закону (1).
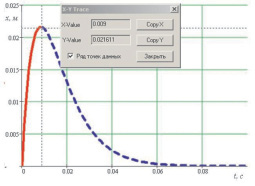
Рис. 2
Такой подход в оценке пластических деформаций заготовок в зависимости от скорости соударения получен впервые.
Рецензенты:
Лебедев А.М., д.т.н., доцент, профессор Ульяновского высшего авиационного училища (института), г. Ульяновск;
Антонец И.В., д.т.н., профессор Ульяновского государственного технического университета им. И.Н. Ульянова, г. Ульяновск.
Работа поступила в редакцию 29.11.2013.