Активно развивающимся направлением науки и техники является внедрение видеокамер для бесконтактного измерения и контроля параметров вибрации техногенных объектов в таких отраслях, как машиностроение, строительство, энергетика [1, 2], когда доступ к объекту контроля затруднен. В связи с этим разработка новых оптических методов контроля параметров вибрации является актуальной научно-технической задачей.
Для измерения параметров гармонической вибрации можно использовать стробоскопический эффект, зафиксированный с помощью ПЗС-фотоприемника [4]. Очевидно, что при кадровой частоте видеокамеры fТВ, равной частоте вибрации объекта f0, наблюдается неподвижное изображение тест-объекта. При этом размах вибрации R можно определить по размытию изображения тест-объекта [6].
Несмотря на то, что изображение вибрирующего тест-объекта при стробоскопическом эффекте неподвижно, оно все-таки отличается от изображения статического тест-объекта своим контрастом на высоких пространственных частотах. Поэтому изображения, возникающие при стробоскопическом эффекте, будем называть квазистатическими. Также следует отметить, что контраст в квазистатическом изображении тест-объекта может существенно изменяться в зависимости от размаха вибрации и времени экспозиции. Для характеристики изменения контраста в изображении тест-объекта в зависимости от изменения пространственной частоты будем использовать частотно-контрастную характеристику (ЧКХ) [5].
Для матричного фотоприемника с размерами дискретных фоточувствительных элементов p×p, мм, когда изображение перемещается в вертикальном направлении, а считывание сигнала осуществляется в горизонтальном направлении, ЧКХ вдоль оси перемещения изображения имеет вид
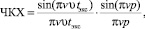(1)
где υ – скорость перемещения изображения тест-объекта относительно фотоприемника; tэкс – время экспозиции; v − пространственная частота парных штрихов; p – размер дискретных фоточувствительных элементов.
Второй сомножитель в формуле (1) характеризует влияние размера дискретного фоточувствительного элемента на контраст в изображении парных штрихов. С целью реализации метода контроля параметров вибрации при калибровке устройства необходимо, чтобы светлый промежуток между штрихами в изображении тест-объекта на самой высокой пространственной частоте составлял 1–2 пикселя, что соответствует его размеру 1p–2p в области фотоприемника. Следовательно, размер A для этой пары штрихов будет равен 2p–4p, и второй сомножитель в (1) для самой высокой пространственной частоты примет постоянное значение 0,64–0,90, то есть будет стремиться к единице. При выполнении этого условия в реализации метода изменение контраста будет определять только первый сомножитель. Задавая время экспозиции у фотоприемника, равное периоду смены кадров, а также принимая во внимание стробоскопический эффект, когда каждая точка тест-объекта за время смены кадров проходит путь S, равный удвоенному размаху вибрации 2R, аргумент синуса в формуле (1) преобразуется к виду
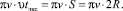(2)
Следовательно, аргумент синуса в формуле (1) будет представлять собой величину, не зависящую от времени.
Учитывая, что размер А = 2а и пространственная частота n = 1/А, из аргумента функции sin(pn∙2R) несложно получить условие возникновения первого нулевого контраста [3]: размах вибрации R должен быть равен ширине штриха а, то есть R = а.
Таким образом, опуская постоянный множитель в (1), изменение контраста в парных штрихах при стробоскопическом эффекте можно записать в виде
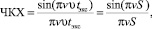(3)
где S – расстояние, на которое перемещаются штрихи тест-объекта за время экспозиции tэкс.
Формула (3) является теоретической основой для контроля размаха вибрации. При кадровой частоте fТВ, равной частоте вибрации f0 (fТВ = f0), а также равенстве времени экспозиции tэкс времени смены кадров ts (tэкс = ts) переход ЧКХ через нуль характеризует возникновение нулевого контраста в изображении парных штрихов с пространственной частотой v, равной [13]:
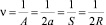. (4)
Согласно формуле (4), при размахе вибрации R = a0 переход ЧКХ через нуль соответствует пространственной частоте:
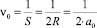(мм–1).
Следовательно, в парных штрихах, имеющих аналогичную пространственную частоту, должен возникать нулевой контраст.
Согласно ЧКХ в изображении парных штрихов, имеющих частоты n менее, чем n0, должен наблюдаться положительный контраст, а в изображении парных штрихов с пространственной частотой выше, чем n0 – отрицательный контраст.
Отмеченный признак – размах вибрации R должен быть равен ширине штриха a изображения тест-объекта, полученного при регистрации стробоскопического эффекта, – может быть использован для контроля размаха гармонической вибрации.
Из формулы ЧКХ (3) видно, что изменение контраста (в том числе и возникающие погрешности) зависят от пути S, пройденного тест-объектом.
Рассмотрим гармонические вибрации тест-объекта с периодом Т0 и размахом R, как показано на рис. 1. Видеокамера регистрирует процесс вибраций за время экспозиции tэкс. Считывание изображений повторяется с периодом смены кадров TТВ. Найдем расстояние S, на которое перемещаются штрихи тест-объекта за время экспозиции tэкс.
Как видно из рис. 1, за время экспозиции tэкс в первом кадре тест-объект пройдет расстояние
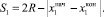
За время экспозиции tэкс во втором кадре расстояние равно
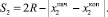
Следовательно, за время экспозиции tэкс в i-м кадре расстояние, пройденное тест-объектом, составит
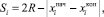(5)
где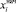 
− начальное положение тест-объекта в i-м кадре; 
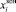− конечное положение тест-объекта в i-м кадре.
Для вычисления значени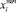й 
и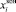 
представим закон вибрации тест-объекта в виде:
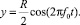
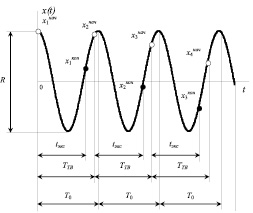
Рис. 1. Представление регистрации пространственно-временного процесса вибраций тест-объекта с помощью линейного датчика видеокамеры
Значение координаты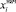 
за время смены кадров TТВ найдем по следующей формуле:
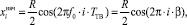(6)
где
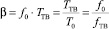(7)
− коэффициент, характеризующий отношение периода смены кадров к периоду вибрации тест-объекта, или частоты вибрации к кадровой частоте видеокамеры.
Для вычисления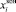 
за время экспозиции tэкс найдем по следующей формуле:
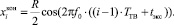(8)
Введем коэффициент g, характеризующий отношение разности периода смены кадров и времени экспозиции к периоду вибраций тест-объекта:
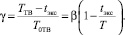(9)
Подставляя (6), (8) в (5) и учитывая коэффициенты (7) и (9), получим расстояние Si, которое проходит тест-объект за время экспозиции tэкс в i-м кадре:
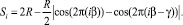(10)
Подставляя Si из (10) в формулу (3), можно вычислить изменения контраста в изображении парных штрихов тест-объекта.
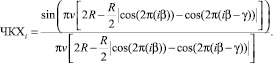(11)
Как видно из формулы (11), если значение Si не изменяется с течением времени, то не будет изменяться и ЧКХ. Однако при изменении Si от кадра к кадру ЧКХi тоже будет изменяться. Этот, на первый взгляд, тривиальный математический вывод иллюстрирует возникновение стробоскопического эффекта.
При регистрации стробоскопического эффекта fТВ ≡ f0 коэффициент β приобретает значение, равное единице. Подставляя значение β в формулу (10), получим упрощенное значение изменения расстояния Si в виде
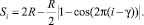(12)
При условии, что tэкс ≡ ts, то есть коэффициент g принимает нулевое значение, имеем простое выражение:
Si = 2R
Следовательно, расстояние, которое проходят парные штрихи в любом i-м кадре, остается неизменным, поэтому и ЧКХi тоже остается неизменной в любой момент времени.
На рис. 2 приведена зависимость расстояния S, которое проходят парные штрихи, от номера кадра для различных значений γ и β при R = 1 о.е. Как видно из этого рисунка, при значениях коэффициентов β = 1 и γ = 0, расстояние, которое проходит тест-объект равно 2 о.е., то есть удвоенному значению размаха вибрации.
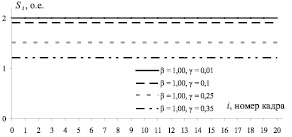
Рис. 2. Зависимость расстояния S, которое проходят парные штрихи, от номера кадра для различных значений γ при β = 0 и R = 1 о.е.
При сохранении значения коэффициента β = 1 и увеличении коэффициента γ = 0,35 расстояние, которое проходит тест-объект, уже не равно удвоенному значению размаха вибрации, оно меньше этого значения, однако вне зависимости от номера кадра расстояние не изменяется. Это объясняется тем, что частота вибрации f0 равна кадровой частоте видеокамеры fТВ, поэтому начальное положение тест-объекта в любом кадре постоянно. При этом даже если время экспозиции не равно периоду смены кадров видеокамеры, то конечное положение тест-объекта в любом кадре будет одним и тем же, хотя и не будет совпадать с начальным положением.
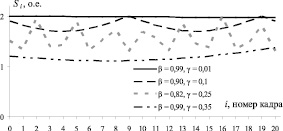
Рис. 3. Зависимость расстояния S, которое проходят парные штрихи, от номера кадра для различных значений β и γ при R = 1 о.е.
На практике добиться равенства частоты вибрации кадровой частоте видеокамеры практически невозможно, приблизиться к этому равенству можно в пределах погрешности измерения, которая определяется шагом изменения периода смены кадров. В связи с этим значение коэффициента β меньше единицы, и значение коэффициента γ больше нуля, хотя и может стремиться к этим значениям.
При значении коэффициента β = 0,99, практически равного единице, характер изменения зависимости пройденного расстояния от номера кадра в зависимости от значения коэффициента γ изменяется.
Если коэффициент γ = 0,01 (рис. 3), то есть близко к нулю, то расстояние, пройденное парными штрихами за период смены кадров, не изменяется во времени и равно удвоенному значению размаха вибрации. Следовательно, при значении коэффициента β = 0,99 и значении коэффициента γ = 0,01 наблюдается стробоскопический эффект.
Если коэффициент γ = 0,35, то есть больше нуля, то расстояние, пройденное парными штрихами за период смены кадров, за различные кадры изменяется и меньше удвоенного значения размаха вибрации. Следовательно, при значении коэффициента β = 0,99 и значении коэффициента γ = 0,35 стробоскопический эффект не наблюдается.
Рассмотрим случай, когда коэффициент β = 0,9 и коэффициент γ = 0,1, то есть время экспозиции не равно периоду смены кадров, их минимальная разница определяется временем оцифровки кадра. Как видно из рис. 3 расстояние S, которое проходят парные штрихи за период смены кадров, периодически изменяется через 10 кадров. Причем за некоторые кадры тест-объект проходит расстояние, равное удвоенному значению размаха вибрации, за некоторые кадры – расстояние, меньшее удвоенного значения размаха вибрации.
При уменьшении коэффициента β до значения 0,82 и увеличении коэффициента γ до значения 0,25 (рис. 4) расстояние S, которое проходят парные штрихи за период смены кадров, постоянно изменяется, причем выделить период изменения из-за дискретности значения номера кадров сложно.
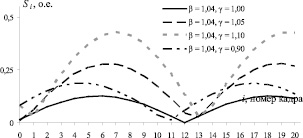
Рис. 4. Зависимость расстояния S, которое проходят парные штрихи, от номера кадра для значений β ≈ 1, γ ≈ 1 и R = 1 о.е.
Из проделанной работы можно сделать вывод, что при равенстве значения коэффициента β = 1 вне зависимости от значения коэффициента γ можно зарегистрировать стробоскопический эффект. На практике добиться равенства значения коэффициента β невозможно, поэтому при значении коэффициента β = 0,99, то есть стремящемся к единице, стробоскопический эффект можно зарегистрировать при значении коэффициента γ = 0,01, то есть стремящегося к нулю, иначе расстояние, которое проходит тест-объект за период смены кадров, изменяется, и стробоскопический эффект зарегистрировать невозможно.
При уменьшении коэффициента β уменьшается и значение функционально зависящего от него коэффициента γ, что приводит к изменению расстояния, которое проходит тест-объект за период смены кадров, во времени, и стробоскопический эффект зарегистрировать также нельзя.
Зафиксировав стробоскопический эффект, можно контролировать частоту вибрации. Измерительным признаком при контроле размаха вибрации является фиксация нулевого контраста в изображении тест-объекта, но для этого необходимо уточнить вид ЧКХ.
Во всех предыдущих случаях для регистрации стробоскопического эффекта задавалось условие β ≈ 1 и γ ≈ 0. Рассмотрим вариант, при котором γ = 1, физический смысл которого заключается в том, что время смены кадров TТВ больше периода вибрации T0 ровно на значение времени экспозиции tэкс. Как видно из формулы (7), значение коэффициента β > 1. В этом случае за время смены кадров TТВ тест-объект переместится в точку, в которой он находился в последний момент фиксации на ПЗС-фотоприемнике видеокамеры tэкс, таким образом каждый кадр будет фиксировать изменение положения тест-объекта, при этом достигается интересный результат: при таких начальных условиях можно получить 1/(β – 1) отсчетов на период T0 при кадровой частоте видеокамеры fТВ, близкой к частоте периодического процесса, в данном случае частоте гармонической вибрации f0.
Учитывая вышесказанное, формула (10), определяющая расстояние Si, которое проходит тест-объект за время экспозиции tэкс в i-м кадре, примет вид:
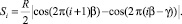(13)
Как видно из рис. 4, при β = 1,04, то есть время экспозиции tэкс в 25 раз меньше периода вибрации T0, и γ = 1,00 зависимость изменения расстояния, пройденного парными штрихами в области фотоприемника, от номера кадра имеет вид синусоиды, повторяя траекторию движения тест-объекта в области объектов.
Отклонение значения коэффициента γ от единицы приводит к изменению расстояния, которое проходит тест-объект за кадр, а также отклонению зависимости расстояния S, которое проходят парные штрихи в области фотоприемника, от траектории движения тест-объекта в области объектов.
Следовательно, для контроля параметров вибрации можно использовать не только регистрацию стробоскопического эффекта при fТВ = f0, При незначительном отклонении кадровой частоты видеокамеры fТВ от частоты гармонической вибрации f0, когда TТВ = T0 + tэкс, можно регистрировать положение тест-объекта, получая 1/(β – 1) отсчетов на период T0.
Рецензенты:
Седалищев В.Н., д.т.н., профессор кафедры «Информационные технологии» Алтайского государственного технического университета им. И.И. Ползунова, г. Барнаул;
Маркин В.Б., д.т.н., профессор, декан естественно-научного факультета Алтайского государственного технического университета им. И.И. Ползунова, г. Барнаул.
Работа поступила в редакцию 29.11.2013.