Рассмотрим основные особенности и приемы сглаживания данных с помощью одномерных сплайнов, оказавшихся эффективными при расчетах сложных геометрических поверхностей. Разработанные авторами методы сглаживания являются актуальными в САПР сложных объектов заготовительно-штамповочного производства [1, 2, 5].
Пусть на сетке Δ:a = x1 < ... < xN = b по заданным значениям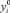 
, i = 1, ..., N построен кубический интерполяционный сплайн S степени n = 2. Известно, что этот сплайн определяется однозначно N – 2 + 2n независимыми параметрами, из которых n параметров связаны условиями единственности сплайна. Поэтому функционал
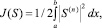(1)
где S(n) – n-я производная сплайна S, является положительной квадратичной функцией N – 2 независимых переменных. Варьируя в допустимых пределах N – 2 независимых параметра, можно уменьшить величину этого функционала и получить в таком смысле более гладкий сплайн, чем исходный.
Для построения такого сплайна, кроме узловых значений функции, необходимы еще два значения ее производных. Если использовать значения вторых производных на концах сетки ∆, то эти условия будут следующими:
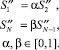
Дополнительные параметры α, β чаще всего принимаются равными единице. В таком случае на последних отрезках сетки Δ получается «чистый изгиб».
При проектировании профиля пера поковки будем использовать кубические сплайны, обеспечивающие необходимую для оболочек Кирхгофа‒Лява непрерывность второй производной, то есть кривизны.
Вернемся к сглаживающим сплайнам. Пусть М – множество сплайнов S, проходящих в «коридоре»:
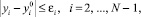(2)
где εi – допустимые отклонения исходных данных в N – 2 узлах сетки ∆. Тогда сплайн S* ∈ М, удовлетворяющий условию
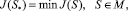(3)
где J(S) определяется по (1), является сглаживающим.
Рассмотрим теперь вариацию функционала J(S) по N – 2 независимым узловым перемещениям, для которых образован коридор (2). Вариация функционала имеет следующий вид:
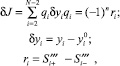(4)
где ri – разрыв старшей производной сплайна в узле i сетки.
Очевидно, функционал J(S) будет уменьшаться, если будут выполняться условия
qiδyi ≤ 0, i = 2, ..., N – 1, (5)
позволяющие определить необходимый знак приращения δyi по знаку реакции qi. Так, если qi > 0, то δyi < 0 и наоборот. В случае qi = 0 нет разрыва старшей производной сплайна, что эквивалентно отсутствию узла i сетки. Отсюда следует, что самый гладкий сплайн не имеет разрывов старшей производной на отрезке (а, в).
Далее, если сглаживающий сплайн в сеточном узле i принимает верхнее предельное положение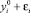 
, то qi ≤ 0, и наоборот. Если такой сплайн занимает промежуточное положение в коридоре, то это, очевидно, эквивалентно отсутствию узла, то есть в этом узле qi = 0.
Данные положения подложены в основу алгоритма построения слаживающих сплайнов. Действительно, так как в узле i сетки сглаживающий сплайн может принимать всего три положения, то множество М содержит 3N–2 элемента. Поскольку сглаживающий сплайн существует, то простым перебором элементов множества его можно найти. Понятно, однако, что такой алгоритм не рационален. Поэтому рассмотрим другие алгоритмы, которые в отличие от некоторых известных алгоритмов [3] обеспечивают сходимость и при этом выполняются условия (2). Существует алгоритм перебора узловых точек сплайна для сглаживания, предложенный С.Л. Березницким [4].
Пусть границы коридора (2) раздвигаются от нуля до предельных значений одновременно при изменении некоторого параметра t от нуля до единицы. В начальный момент строится исходный сплайн S и определяются величины qi во всех узлах i = 2,..., N – 1. Далее, если qi > 0, то узел i «прикрепляется» к нижней подвижной границе, если qj < 0 – к верхней. В случае qi = 0 узел «освобождается».
В закрепленных узлах принимается, что
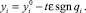(6)
При данном наборе закрепленных узлов коэффициенты qi и уi линейно зависят от t.
На втором шаге назначается t = t1 < 1 и строится соответствующий сплайн. По значениям qi, i = 2, ..., N – l на основе указанной линейности определяются парамет ры t(i), i = 2,... , N – 1, при которых:
1) в закрепленном узле величина q; сменит знак;
2) свободный узел i пересечет предельную границу «коридора».
Затем выбирается t* = min t(i) и строится новый сплайн по значению параметра t2 = t*. В полученном сплайне узлы с qi = 0 отпускаются, а узлы, пересекающие предельную границу, прикрепляются к ней.
Далее все повторяется. Если окажется, что наименьшее значение t* > 1, то принимается t* = l, границы принимают предельное положение, а соответствующий сплайн является сглаживающим. Если все qi = 0, i = 2, ..., N – 1, то процесс также прекращается.
Этот алгоритм является трудоемким при пересчете, поэтому можно ввести упрощения, разработанные авторами.
На первой итерации по заданным значениям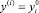 
, i = 2, ..., N – 1 строится исходный сплайн и вычисляются коэффициенты qi. На второй и последующих итерациях узловые значения сплайна вычисляются по формуле
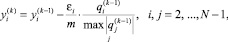(7)
где m ‒ назначаемое целое число, определяющее погрешность построения сглаживающего сплайна. Далее строится соответствующий сплайн.
На каждой итерации контролируется условие:
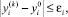i = 2, ..., N – 1. (8)
И если оно нарушается в узле I, то в нем принимается соответствующее предельное значение. Поскольку здесь узлы с нулевой реакцией qi не «отпускаются», то приходится проверять основное условие: δJ ≤ 0 Если оно нарушается, то шаг итерации дробится, т.е. вместо числа m принимается 2m, и вновь строится сплайн. В результате получаем сглаживающий интерполяционный сплайн. Результаты использования этого 1 алгоритма показаны в таблице.
Существует еще один алгоритм [3] построения интерполяционных сглаживающих сплайнов. В нем речь идет о минимизации функционала вида:
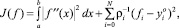(9)
где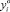 
– ординаты исходных данных, ρi > 0 – заданный весовой коэффициент.
Заметим, что если все ρi = 0, то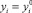 
, i = 0, ..., N и сглаживающий сплайн превращается в интерполяционный. Отсюда следует, что чем точнее заданы 
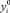в узлах сетки, тем меньше должны быть весовые множители ρi. В частности, если возникнет необходимость закрепить точку с номером 1, то надо принять ρi = 0.
Сглаживающий сплайн S(x) должен удовлетворять условиям:
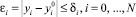(10)
или
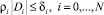, (11)
где δi – допустимый «коридор» заданных значений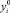 
, который на практике задается технологом и обычно берется равным 20 % допуска на припуск по эквидистанте пера.
Строится итерационный процесс, реализация которого позволяет получить множители ρi, i = 0, ..., N
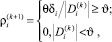(12)
где k – номер итерации. Коэффициенты D рассчитываем матричным способом [4].
Следующим шагом находится yi:
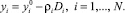(13)
Итерационный процесс продолжается до тех пор, пока значения сплайна в узлах сетки не окажутся в допустимом «коридоре».
Однако в работе [3] не приводится четких рекомендаций по выбору коэффициентов θ и ϑ, что затрудняет практическое применение этого алгоритма. Результаты работы второго алгоритма находятся в таблице.
Можно использовать алгоритм сглаживания интерполяционными кубическими сплайнами с описанием массива узловых точек, предлагаемый авторами. По этому алгоритму последовательно корректируется положение каждой точки массива, кроме одной из осей. На рисунке показана графическая модель сплайна.
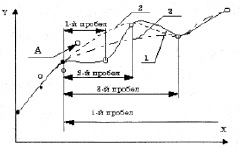
Графическая модель сплайна
Пусть сначала корректируется положение точки А. На первом этапе эта точка исключается из общего массива, в результате чего образуется 1-й пробел. Интерполяционный сплайн 1, построенный по оставшимся узловым точкам, показывает величину ее коррекции. На следующих этапах пробел увеличивается за счет включения в него нарастающего числа точек. Возникающие при этом новые сплайны (2, 3 … i) позволяют рассчитать поэтапную коррекцию. Значение этой величины принимается равным среднеарифметическому ее поэтапных величин. Выбор длины максимального пробела зависит от кривизны профиля и шага базовых точек. Математическая модель интерполяционного сплайна берется из теории сплайн – функций [3].
Кубический сплайн имеет вид:
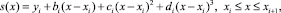(14)
на каждом подынтервале
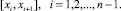
Эти коэффициенты выражаются формулами:
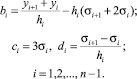
σi находится из системы:
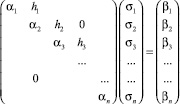. (15)
Здесь диагональные элементы αi вычисляются по формулам:
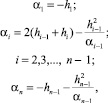
а правые части βi – по формулам
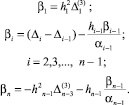
Наконец, коэффициенты σi определяются посредством обратной подстановки:
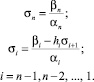
Эту систему из n уравнений можно решить методом исключения. Для вычисления неизвестных σi можно использовать написанные программы. С помощью другой программы можно вычислять значения сплайна.
На каждом шаге итерации оставшиеся точки апроксимируются кубическим сплайном, что позволяет рассчитывать n новых скорректированных значений рассматриваемой точки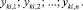 
Отклонения новых значений координат точки от исходных определяются из отношений:
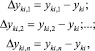(16)
где уki – исходная координата рассматриваемой точки в i-й итерации.
Новая координата рассматриваемой точки находится из выражения:
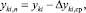(17)
в котором
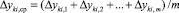
– среднее отклонение.
В результате корректировки любая точка массива не должна выходить за пределы ранее установленного «коридора», т.е.
\ук0 – ykj| < ε.
Если условие не выполняется, то точка смещается на допустимое значение ε. Количество итераций сглаживания ограничивается условием: δJ → 0.
Расчеты по описанному алгоритму показали, что хорошие результаты достигаются, если максимальная длина пробела равна трем точкам исходного массива.
Для сравнительной оценки эффективности сглаживания по рассмотренным алгоритмам был реализован численный расчет. Результаты расчетов для массива точек спинки пера заготовки с шагом 0,05 по рассмотренным алгоритмам сглаживания приведены в таблице.
Результаты сглаживания и их оценочные показатели
|
X |
Y |
уисх (округленные) |
у 1 (1 алгоритм) |
у2 (2 алгоритм) |
у3 (3 алгоритм) |
|
0,80 |
2,2255 |
2,2 |
2,2169 |
2,2121 |
2,2238 |
|
0,85 |
2,3396 |
2,3 |
2,3276 |
2,3311 |
2,3485 |
|
0,90 |
2,4596 |
2,5 |
2,4788 |
2,4557 |
2,4734 |
|
0,95 |
2,5857 |
2,6 |
2,6042 |
2,5849 |
2,5925 |
|
1,00 |
2,7183 |
2,7 |
2,7000 |
2,7186 |
2,7000 |
|
Значение функционала |
5910,3 |
990,5 |
96,9 |
67,5 |
|
|
Кол. итераций |
30 |
32 |
6 |
Из таблицы видно, что хорошие результаты сглаживания достигаются при расчетах по 2-му и 3-му алгоритмам. Это согласуется с численными значениями функционалов. Следует отметить, что расчеты по 3-му алгоритму приводят к удовлетворительным результатам за меньшее количество итераций, т.е. его сходимость является максимальной.
Рецензенты:
Попов И.П., д.т.н., профессор кафедры «Обработка металлов давлением», СГАУ, г. Самара;
Михеев В.А., д.т.н., профессор кафедры «Обработка металлов давлением», СГАУ, г. Самара.
Работа поступила в редакцию 22.11.2013.