Свойство древесины усиливать звук без искажения тона называется резонансной способностью [1]. В свою очередь древесина, которая обладает данной способностью, называется резонансной. Она используется, главным образом, в музыкальной промышленности: для изготовления дек музыкальных инструментов, внутренней отделки концертных залов и т.д.
В настоящее время приходится сталкиваться с проблемой нехватки древесины с уникальными резонансными свойствами. Этот материал является весьма дорогим: стоимость кубометра сертифицированной резонансной ели составляет 50–70 тыс. рублей. Более того, затруднено определение резонансных свойств среди растущих деревьев, что может привести к нерациональному и убыточному использованию и без того редкого сырья в качестве обычного сортимента. Ситуация также усугубляется отсутствием диагностики акустических свойств древесины как в зрелом возрасте к моменту рубки, так и молодняков. Поэтому имеется необходимость целевого выращивания резонансных деревьев и проведения диагностики их древесины еще в стадии подроста. Данная проблема решается на базе «Учебно-опытного лесхоза» и «Лаборатории квалиметрии резонансной древесины» при кафедре стандартизации сертификации и товароведения ПГТУ.
Резонансные свойства характеризуются акустической константой К [7]
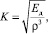(1)
где Ед – динамический модуль упругости, Н/м2; r – плотность древесины, кг/м3.
Для того чтобы рассчитать акустическую константу, необходимо найти динамический модуль упругости и плотность древесины. Существующие стандартные методы нахождения модуля упругости [4, 5] не подходят для ранней неразрушающей диагностики дендроакустических свойств. Поэтому целью нашей работы являлся поиск оптимального неразрушающего способа определения дендроакустических свойств молодняков.
Цели исследования
- Выполнение экспериментальных исследований по определению акустических показателей древесины тремя способами: ультразвуковым, виброакустическим и статическим.
- Обоснование достоверности результатов экспериментов данным численного анализа, полученных методом конечных элементов (МКЭ).
- Провести статистическую обработку результатов исследований и оценить точность данных способов.
- Анализ преимуществ и недостатков рассматриваемых способов. Выбор наиболее точного и эффективного способа.
Для экспериментальных исследований использовались образцы из древесины березы цилиндрической формы. Влажность образца в момент испытания составила 6,8 %. Измерения проводились в соответствии со следующими стандартами:
- влажность древесины по ГОСТ 16483.7-71;
- плотность древесины по ГОСТ 16483.1-84;
- исследования на стандартном образце по ГОСТ 16483.0-89.
При диагностике упругих свойств образцов использован ультразвуковой метод, а также вибрационный (резонансный) и статический.
Ультразвуковой метод
Метод состоит в измерении времени прохождения звуковой волны t вдоль деревянного образца длиной l на приборе УК-14П и вычислении скорости прохождения звука c, посредством которой возможно определение динамического модуля упругости Ед вдоль волокон (2) и акустической константы К (3) [6, 7]. Результаты измерений и вычислений представлены в табл. 1.
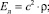(2)
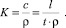(3)
Таблица 1
Определение упругих свойств ультразвуковым способом
|
Номер образца |
Время прохождения звуковой волны t, мкс |
Скорость звука с, м/с |
Модуль упругости Ед, ГПа |
Акустическая константа К, м4/(кг·с) |
|
1 |
17,5 |
5731 |
19,78 |
9,5 |
|
2 |
17,5 |
5731 |
19,78 |
9,5 |
|
3 |
17,4 |
5764 |
20,01 |
9,6 |
|
4 |
17,2 |
5831 |
20,48 |
9,7 |
|
5 |
17,6 |
5698 |
19,56 |
9,5 |
|
6 |
17,3 |
5797 |
20,24 |
9,6 |
|
7 |
17,4 |
5764 |
20,01 |
9,6 |
|
8 |
17,4 |
5764 |
20,01 |
9,6 |
|
9 |
17,5 |
5731 |
19,78 |
9,5 |
|
10 |
17,2 |
5831 |
20,48 |
9,7 |
|
Рабочая длина образцов l = 100,3 мм; диаметр d = 2,96 мм; плотность ρ = 596,1 кг/м3 |
||||
Виброакустический метод
Основан на выявлении собственной (резонансной) частоты образца f при пропускании через образец детерминированного звукового сигнала с повышающейся частотой и определении Ед с учетом его рабочей длины l, диаметра d и объемного веса γ, а также константы К по формуле (1) [3, 8].
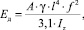(4)
где А – площадь поперечного сечения; γ – удельный вес; Iz – момент инерции поперечного сечения. Результаты представлены в табл. 2.
Численный анализ
С целью численной проверки достоверности экспериментальной методики по определению низшей собственной частоты образцов использована расчетная стержневая модель, построенная на базе метода конечных элементов (МКЭ) [6]. Древесина представляется на основе модели ортотропного тела. Для описания ее упругих свойств использованы данные из табл. 2, а также справочные физико-механические характеристики:, Gar = 1,095 МПа, μra = 0,038 [6]. Индекс «a» соответствует направлению вдоль волокон древесины, индекс «r» – радиальному направлению. Построенная дискретная модель из 10 конечных элементов (КЭ) представлена на рис. 1. Защемление стержня моделировалось запрещением линейных и угловых перемещений крайнего узла.
Используя КЭ построенную модель, решена задача динамики, которая описывается системой обыкновенных дифференциальных уравнений
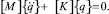(5)
Здесь [M], [K] – матрицы масс и жесткости конструкции;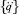 
, {q} - векторы обобщенных ускорений и перемещений соответственно. Порядок матриц равняется числу степеней свободы n = 35.
Рис. 1. Конечно-элементная модель
Для расчета низшей собственной частоты и формы колебаний использован метод итераций в подпространстве собственных векторов. Колебательные движения образца представляются суперпозицией низших собственных форм:
.
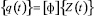Здесь [Ф] = [j1, j2…, j5] - матрица, составленная из пяти низших собственных форм, {Z(t)} - главные или нормальные координаты. В этом случае уравнения (5), записанные в главных координатах, становятся разделяющимися относительно них и принимают вид:
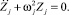(6)
Здесь wj - круговая частота для j-й собственной формы. Для дискретизации образца используются трехузловые КЭ с 3 степенями свободы в узле. Задача решена с использованием моделей различной степени дискретизации. Во всех случаях получены одинаковые результаты, что означает достаточно высокую степень сходимости результатов МКЭ. Уже при дискретизации на 10 КЭ точность расчетов оказывается достаточно удовлетворительной. Программный комплекс позволил проанализировать результаты в графическом виде: построена низшая форма колебаний (рис. 2). Результаты расчета сведены в табл. 2.
Рис. 2. Первая форма колебаний образца
Таблица 2
Определение упругих свойств виброакустическим способом
|
Номер образца |
Резонансная частота f, Гц |
Модуль упругости Eд, ГПа |
Акустическая константа K, м4/(кг·с) |
|
|
Решение МКЭ |
Эксперимент |
|||
|
1 |
123 |
119 |
2,14 |
3,13 |
|
2 |
124 |
120 |
2,18 |
3,16 |
|
3 |
124 |
120 |
2,18 |
3,16 |
|
4 |
124 |
120 |
2,18 |
3,16 |
|
5 |
124 |
120 |
2,18 |
3,16 |
|
6 |
124 |
120 |
2,18 |
3,16 |
|
7 |
124 |
120 |
2,18 |
3,16 |
|
8 |
124 |
120 |
2,18 |
3,16 |
|
9 |
124 |
120 |
2,18 |
3,16 |
|
10 |
124 |
120 |
2,18 |
3,16 |
|
Рабочая длина образцов l = 80,2 мм; плотность ρ = 602,1 кг/м3 |
||||
Анализ табличных данных показывает соответствие результатов расчета экспериментальным данным. Это означает правильность методики эксперимента. Вместе с тем видно, что величина модуля упругости оказывается существенно заниженной по сравнению с известными значениями [2]. Видимо, это связано с заниженным экспериментальным значением собственной частоты колебаний образца, что является следствием несовершенства технических элементов устройства [8]. Данная проблема может быть решена введением поправочного коэффициента при экспериментальном определении собственной частоты.
Статический метод
Методика предполагает измерение максимальной стрелы прогиба v образца при его консольном креплении и последующем расчете модуля упругости и акустической константы (7), (8) [7]. Результаты измерений представлены в табл. 3.
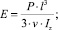(7)
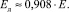(8)
Здесь Р – вес подвешиваемого на образец груза, Н.
Таблица 3
Определение упругих свойств статическим способом
|
Номер образца |
mгр., г |
l, мм |
v, мм |
Iz, мм4 |
Е, ГПа |
Ед, ГПа |
K, м4/(кг∙с) |
|
1 |
10,90 |
79,9 |
0,10 |
3,77 |
48,2 |
43,8 |
14,4 |
|
2 |
17,36 |
79,9 |
0,50 |
3,77 |
15,4 |
13,9 |
8,13 |
|
3 |
23,92 |
79,9 |
0,96 |
3,77 |
11,0 |
10,0 |
6,89 |
|
4 |
30,50 |
79,9 |
1,27 |
3,77 |
10,6 |
9,64 |
6,76 |
|
5 |
36,57 |
79,9 |
1,71 |
3,77 |
9,47 |
8,59 |
6,38 |
|
6 |
42,91 |
79,9 |
1,98 |
3,77 |
9,6 |
8,70 |
6,42 |
|
7 |
49,35 |
79,9 |
2,30 |
3,77 |
9,49 |
8,62 |
6,39 |
|
8 |
55,80 |
79,9 |
2,64 |
3,77 |
9,35 |
8,49 |
6,34 |
|
9 |
62,33 |
79,9 |
3,01 |
3,77 |
9,16 |
8,31 |
6,28 |
|
10 |
68,81 |
79,9 |
3,33 |
3,77 |
9,14 |
8,30 |
6,27 |
Статистический анализ
По полученным данным был проведен статистический анализ: оценены погрешности измерений и точность способов. Значения акустической константы, найденные разными способами, весьма отличаются друг от друга (табл. 4). Видно, что К при испытаниях ультразвуком наибольшая, виброакустическим способом – наименьшая. Также была проведена оценка погрешности каждого из способов и, соответственно, их точность. Результаты приведены в табл. 4.
Таблица 4
Статистический анализ данных
|
Характеристики измерения акустической константы К |
Ультразвуковой способ |
Виброакустический способ |
Статический способ |
|
Расчетное значение, м4/(кг∙с) |
9,57 |
3,16 |
6,27 |
|
СКО, м4/(кг∙с) |
0,0893 |
0,0140 |
0,0998 |
|
Дисперсия, м8/(кг∙с)2 |
0,000069 |
0,000196 |
0,009960 |
|
Показатель точности, % |
0,29 |
0,14 |
0,50 |
|
Доверительная ошибка, м4/(кг·с), Р = 95 % |
0,053 |
0,032 |
0,2255 |
|
Относительная погрешность, % |
0,6 |
1,0 |
3,5 |
|
Коэффициент корреляции |
–0,2066 |
||
|
Критерий Фишера, Р = 95 % |
2,84 < 3,21 – дисперсии однородны |
||
Заключение
Итак, меньшей погрешностью и большей точностью обладает виброакустический способ измерения. Более грубые ошибки получены при использовании способа статического изгиба. Проверена корреляция между ультразвуковым и виброакустическим способами. Сильной корреляционной связи между ними не выявлено (r = –0,2066). Между тем дисперсии выборок этих двух методов оказались однородными. На данном этапе исследований установлено, что наиболее приемлемым способом диагностики акустических свойств деревьев в молодом возрасте является виброакустический с использованием установки типа «Резонанс-4» [8], так как он дает быстрые результаты c небольшой доверительной ошибкой. Однако при этом для получения корректных результатов возникает необходимость введения поправочных коэффициентов. Вероятно, что существуют или могут быть разработаны иные способы идентификации, поэтому исследования в данном направлении целесообразно продолжать.
Работа выполнена при поддержке гранта РФФИ № 13-01-97045 р_поволжье_а.
Рецензенты:
Войтко П.Ф., д.т.н., профессор, декан лесопромышленного факультета, ФГБОУ ВПО ПГТУ, г. Йошкар-Ола;
Царев Е.М., д.т.н., профессор кафедры «Технология и оборудование лесопромышленных производств», ФГБОУ ВПО ПГТУ, г. Йошкар-Ола.
Работа поступила в редакцию 22.11.2013.