Исследования широкого класса экономических систем, в первую очередь систем массового обслуживания (СМО) осуществляется в основном в условиях стационарности потоков (простейшие, эрланговские и др.). СМО с простейшими потоками, как известно [1], описываются системами линейных дифференциальных уравнений Колмогорова с постоянными коэффициентами. Обычно, когда уравнений достаточно много и характерное время переходных процессов существенно меньше периода функционирования системы, интересуются только асимптотикой поведения решения, то есть так называемыми стационарными распределениями вероятностей состояний, возникающими при длительном наблюдении системы (t → ∞). В классическом случае такие решения выражаются формулами Эрланга и аналогичными им. Однако практически это означает, что системы, интервал наблюдения которых оказывается меньше интервала сходимости, не могут быть описаны адекватно стационарным распределением. Кроме того, интенсивности потоков в процессе функционирования могут медленно или скачкообразно изменяться. В этих условиях моделирование сводится к построению модели многомерной динамической системы с изменяющимися параметрами. Кроме этого, иногда необходимо построить модели СМО реального времени. В теории массового обслуживания такие модели, по сведениями авторов, не известны. Необходимость вычислений в реальном масштабе времени при сохранении приемлемой точности требует применения техники параллельных вычислений, основанной на матричных преобразованиях.
Цель работы. В соответствии со сказанным целью работы является алгоритмизация процедуры численного моделирования непрерывных процессов в СМО, исходя из их представления размеченными графами состояний и переходов. Для решения этой задачи нами предлагается наглядный способ составления численных схем итеративного матричного процесса с использованием теории сигнальных графов. Необходимость дать простой хорошо структурированный способ построения численной схемы решения дифференциальных уравнений Колмогорова диктуется, в частности, отсутствием у специалистов по экономике сферы обслуживания специальных знаний по численным методам моделирования непрерывных процессов. Способ основан на идее аналогового моделирования [6, 4] обыкновенных дифференциальных уравнений.
Методика построения численного представления схемы аналогового интегратора
Как известно, решение дифференциального уравнения (ДУ) на аналоговой вычислительной машине (АВМ) достаточно подробно разработано (например, работа [5]). Аналоговый интегратор обычно обозначается особым знаком 
(рис. 1), а выполняемое им преобразование может быть представлено в виде выражения
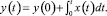
Типовые звенья АВМ при программировании соединяются согласно разрабатываемой структурной схеме. При этом сформулированная задача в форме Коши вида (1) приводится к виду (2), на основе чего формируется структура вычислительной сети, представленной на рис. 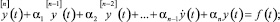1.
(1)
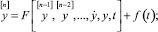
при начальных условиях
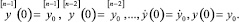(2)
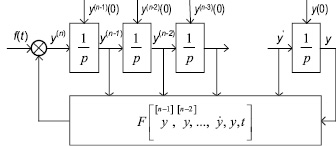
Рис. 1
Приведенная структурная схема решения ДУ на АВМ является основой для построения её численного аналога, предлагаемого авторами.
Рассмотрим один интегратор, который находится в момент t0 в начальных условиях y(t0), и на его вход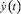 
«подаётся» величина f(t)
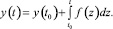
Простейшая численная схема интегратора, построенная по методу прямоугольников, имеет вид
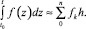(3)
Очевидно, что итерационная формула интегрирования будет иметь вид
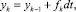(4)
где h = dt, а fk – отсчет функции f(tk) при tk = tk-1 + dt.
Ясно, что (3) формально означает вычисление значений первообразной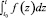 
по значению производной, поэтому выражению (4) соответствует сигнальный граф преобразования 
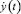в y(t) за один шаг вычислительного процесса, представленный на рис. 2. Это и есть численный интегратор, который при dt → 0 в пределе, как известно [2], дает ломаную Эйлера, сколь угодно близкую к интегральной кривой.
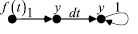
Рис. 2
Интегратору, представленному этим сигнальным графом, можно сопоставить переходную матрицу, которая описывает на шаге превращение вектора–строки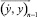 
в вектор–строку 
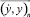. Заметим также, что в действительности (4) отражает тот факт, что настоящие состояния любой системы есть следствия некоторой «вынуждающей силы» и непосредственно предшествующих состояний. Это означает, что в простейшем случае процесс получения численных решений дифференциального уравнения является причинным (или марковским [3] – т.е. без предыстории) с переходной матрицей, такой, что:
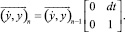(5)
Методика использования рассмотренного интегратора для моделирования д.у. сводится к следующему.
1. Исходное уравнение (1) разрешается относительно старшей производной, т.е. приводится к виду (2).
2. Вычерчивается часть структурной схемы, на которой изображается цепочка из последовательно включенных численных интеграторов (рис. 2), число которых равно порядку дифференциального уравнения.
3. На основании полученной цепочки строится сигнальный граф, вершины которого соответствуют последовательно соединенным входам и выходам интеграторов. При этом вершинам интеграторов соответствуют значения производных, фигурирующих в уравнении с последовательно понижающимся порядком вплоть до исходной переменной на выходе последнего в цепочке интегратора.
4. Строится граф функционального преобразователя, соответствующего правой части выражения (2). Конкретный вид этой схемы определяется заданным аналитическим выражением функции F[.].
5. Выход схемы, реализующей F[.], подается на вход первого численного интегратора графа. Установление такой связи математически соответствует приведению к равенству (материальному выравниванию) правой и левой частей уравнения (2). Если уравнение содержит независимую функцию времени (вынуждающую силу), то эта функция суммируется на входе цепочки интегратора с выходным сигналом преобразователя F[.] (как это представлено в (2)).
6. По полученной структуре сигнального графа численного решения формируется переходная матрица, порядок которой равен порядку дифференциального уравнения (числу интегрирующих вершин). Переходная матрица позволяет записать рекуррентное отношение вычисления вектора переменных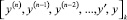 
на шаге k, в общем случае с учетом значения f[k].
7. Начальным условиям соответствует вектор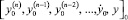 
, со значений которого начинается вычислительный процесс.
Получаемый по предложеной методике сигнальный граф предлагается назвать интегрирующим сигнальным графом.
Пример применения методики. Пусть задано уравнение линейного осциллятора:
Действуя по предложенной методике, получим сигнальный граф вида рис. 3. Графу на рис. 3 соответствует переходная матрица 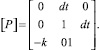(6).
(6)
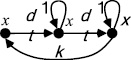
Рис. 3
Модель, изображенная графом на рис. 3 и представленная матрицей (6), описывает линейный осциллятор без потерь. Динамику свободного движения этого осциллятора можно описать в виде следующего преобразования
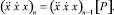
Удобство метода матричного моделирования д.у. состоит еще и в том, что вектор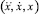 
сразу даёт решение как последовательность точек фазового портрета динамической системы.
Численное моделирование процессов массового обслуживания
В некоторых случаях возникает необходимость исследовать работу системы массового обслуживания при отсутствии стационарного режима или когда такой режим ещё не наступил. Как правило, постановка задачи в такой форме означает, что время функционирования системы меньше времени окончания переходного процесса или сопоставимо с ним по длительности (СМО в здравоохранении, торговле и т.д.).
При наблюдении СМО с заданной длительностью рабочего периода (рабочего дня) режим работы изменяется скачком в процессе рабочего цикла либо интенсивности потоков в течении рабочего периода системы могут существенно меняться. Это означает, что в системе постоянно происходят переходные процессы от одного стационарного режима к другому. В некоторых изучаемых системах возможен случай, когда рабочий период системы существенно меньше времени переходного процесса.
Предложенный выше способ моделирования динамических систем на основе интегрирующих сигнальных графов позволяет получить относительно простой и наглядный способ решения за счет упрощения перехода от размеченного графа системы непосредственно к численной схеме интегрирования.
Дополнительным преимуществом предложенного метода является то, что матричные вычисления большой размерности и с большим числом шагов, которые требуются для более точных вычислений по методу Эйлера, легко реализуются на современных многопроцессорных компьютерах. Это обусловлено тем, что матричные алгоритмы позволяют достаточно легко провести векторизацию вычислений, а в некоторых случаях и их распараллеливание. Такой подход к построению алгоритмов вычислений позволяет также исследовать поведение систем в реальном масштабе времени.
Алгоритм численного моделирования системы дифференциальных уравнений Колмогорова, общего для классических СМО и для процесса гибели–размножения, включает следующие этапы.
1. Строится размеченный граф процесса.
2. Для каждого состояния графа по известным правилам записывается дифференциальное уравнение Колмогорова [1].
3. Для каждого уравнения (вершины размеченного графа состояния) вычерчивается интегратор.
4. По дифференциальным уравнениям системы, которые в соответствии с канонической формой Колмогорова уже разрешены относительно старших производных, значения этих производных приравниваются правым частям, то есть проводятся стрелки с передачами и направлениями, соответствующими суммируемым интенсивностям и направлениям действия потоков.
5. Составляется алгоритм вычисления всех значений вероятностей и их производных в матричной форме.
При использовании алгоритма необходимо иметь в виду следующее. При составлении уравнений Колмогорова считается, что все потоки действуют на скорости изменения вероятностей, то есть только на их первые производные по времени. Поскольку вытекающие потоки уменьшают вероятности, они воздействуют на соответствующую производную со знаком минус. Эти воздействия имеют причинно-следственный характер, поэтому невозможно, например, инвертировать дуги, как может показаться на первый взгляд.
Рассмотрим пример моделирования процесса, имеющего 3 состояния. Схема процесса гибели–размножения, включающая три состояния, имеет вид, представленный на рис. 4, а.
Система дифференциальных уравнений Колмогорова для приведенной схемы представленная выражениями 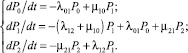(7).
(7)
Структурная схема численной модели, содержащая три интегратора, представлена сигнальным графом, изображенном на рис. 4, б. Данному графу может быть сопоставлена матрица передач, соответствующая линейному оператору пересчета вектора вероятностей и их производных за один шаг времени dt.
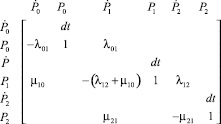(8)
а 
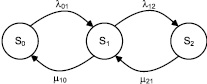б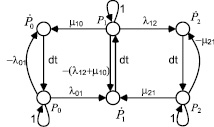
Рис. 4
Уравнение изменения вероятностей на шаге интегрирования будет иметь вид
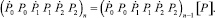(9)
Рассмотрим численный пример. Пусть даны следующие значения величин потоков: l01 = 1, l12 = 1, m10 = 1, m21 = 1, dt = 0,0001. Начальное распределение p = (0; 0,5; 0; 0,3; 0; 0,2). Тогда при числе шагов N = 50000 получим следующий график, представленный на рис. 5, а). При тех же интенсивностях потоков размножения l01 = 1, l12 = 1 и других интенсивностях потоков смертности m10 = 2, m21 = 2 получим, очевидно, другое решение (рис. 5, б).
Аналитические выражения для стационарных вероятностей имеют для нашего случая вид:
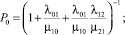
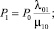
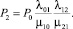(10)
а 
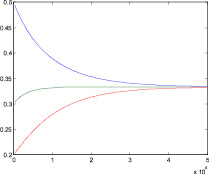б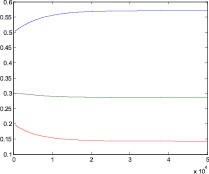 
Рис. 5
Для первого набора начальных условий по формулам (10) получаем: P0 = P1 = P2 = 1/3. Для второго набора получаем: P0 = 4/7 ≈ 0,57142857, P1 = 2/7 ≈ 0,28571423, P2 = 1/7 ≈ 0,142867143.
Отметим, что сумма стационарных вероятностей всегда равна единице, что соответствует условиям нормировки, обычно принимаемой при нахождении стационарного решения обычным путем. Как видно с достаточно высокой точностью, полученные решения системы дифференциальных уравнений асимптотически стремятся к этим значениям.
Заключение
Предложенная графоаналитическая методика для составления численных схем решения систем линейных дифференциальных уравнений, как показывает практика, является достаточно удобным инструментом исследования переходных режимов работы реальных систем, в частности, СМО. Такие режимы наблюдаются в течение работы таких систем как лечебно-профилактические учреждения, режим работы которых можно разбить на несколько участков стационарности.
Рецензенты:
Верхотуров М.А., д.т.н., профессор кафедры ВМиК, ФГБОУ ВПО УГАТУ, г. Уфа;
Мунасыпов Р.А., д.т.н., профессор кафедры технической кибернетики, ФГБОУ ВПО УГАТУ, г. Уфа.
Работа поступила в редакцию 22.11.2013.