Необходимость изучения интегрированных структур в агропромышленном комплексе связана с изменениями производственных отношений, социально-политических и организационно-экономических условий производства, формированием многоукладной экономики, развитием рынка, что влечет за собой изменения структур и механизмов взаимодействия предприятий агропромышленного комплекса.
По нашему мнению, одним из возможных инструментов устойчивого развития регионального агропромышленного комплекса может стать формирование такой региональной интегрированной структуры, как агропродовольственный кластер, который будет являться своеобразным локомотивом динамичного развития сельского хозяйства и перерабатывающей промышленности, и служить повышению уровня и качества продовольственного обеспечения населения региона. Кроме того, «…формирование агропромышленных кластеров может стать одним из перспективных направлений как в решении стратегических задач в агропродовольственной сфере, так и в повышении устойчивости экономического развития региона» [1]. Обоснование целесообразности формирования агропродовольственного кластера, как сложной социально-экономической системы, должно базироваться на использовании системного подхода, суть которого заключается в использовании концепции оптимизации денежных потоков доходов и расходов основных экономических агентов, заинтересованных в эффективном функционировании агропродовольственного кластера региона. «Системный подход к продовольственной самообеспеченности – это совокупность и комплексное использование таких подходов в деятельности АПК, как структурный, инвестиционный, управленческий, финансово-бюджетный и ряд других» [2; 3].
Для решения описанной выше задачи требуется разработка математических моделей управления сельскохозяйственной отраслью, ее подсистемами или интегрированными структурами для оценки эффективности их деятельности.
Содержательная постановка задачи
При разработке моделей крупных социально-экономических систем и оценке эффективности их функционирования, в связи с наличием множества влияющих на это факторов, возникают проблемы взаимной увязки операционных, инвестиционных, финансовых потоков экономических агентов в них, что, в частности, порождает необходимость использования большого количества данных, используемых в процессе моделирования. Для обработки данной информации необходимо использовать автоматизированные средства анализа, эффективность применения которых зависит от сбалансированности математических моделей, лежащих в основе алгоритмов ее обработки.
При этом используются либо имитационные, либо оптимизационные математические модели. В имитационных моделях подробно описываются инвестиционные, производственные и финансовые потоки указанных структур, что требует большого количества численных экспериментов. При этом не решается задача оптимизации потоков и не гарантируется получение даже квазиоптимального сценария. В оптимизационных моделях результат функционирования социально-экономической системы описывается, как правило, в виде упрощенных производственных функций, что в значительной степени не устраивает экономистов-аналитиков. В данной работе предлагается основанная на оптимизационно-имитационном подходе [4] гибридная математическая модель в форме линейной задачи оптимизации. В указанной модели, при формировании доходных и расходных характеристик экономических агентов (производителя, потребителя, налогового органа), используется достаточно универсальный алгоритм, соответствующий существующим правилам расчета прибыли, амортизации, налоговых и прочих затрат производителя, а также оплаты труда потребителя и налоговых сборов управляющего органа.
Для обоснования целесообразности формирования агропродовольственного кластера модифицируется математическая модель реальных инвестиций, опубликованная в работе [5]. В указанной работе в качестве основного критерия эффективности функционирования экономической системы (агропродовольственного кластера) выбирается дисконтированное сальдо ее доходных и расходных потоков.
Математическая постановка задачи
Введем следующие обозначения:
yk – объем производства по k-му виду сельскохозяйственной продукции, тыс. т;
mk – количество приобретаемых основных производственных фондов для производства k-го вида сельскохозяйственной продукции, ед.;
qk – прогнозный спрос на продукцию k-го вида в стоимостном выражении, рублей;
Vk – проектная производительность основных производственных фондов по k-му виду;
Тk – срок службы основных производственных фондов k-го вида, лет;
Pk – стоимость единицы продукции k-го вида, рублей;
Т – срок действия (горизонт планирования), лет;
ck – среднегодовая стоимость основных производственных фондов k-го вида сельскохозяйственной продукции, рублей;
xk = ckmk (k = 1, ..., n) – инвестиции (стоимость, вложения для поддержания в рабочем состоянии) приобретаемых основных производственных фондов k-го типа, рублей;
xn+k = Pkmkyk (k = 1, ..., n) – выручка от продажи продукции k-го вида, рублей;
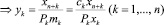– выпуск продукции k-го вида, т;
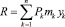– суммарная выручка от реализации по всем видам продукции;
F = βR – фонд оплаты труда, определяемый как заданный экспертно процент β выручки от реализации R всей продукции;
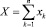– суммарные инвестиции в приобретение основных производственных фондов;
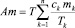– сумма амортизационных отчислений за весь горизонт планирования Т по всем видам основных производственных фондов, рублей;
z – суммарные материальные затраты, определяемые в виде заданного процента от общих затрат деятельности агропродовольственного кластера, рублей;
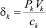– относительный показатель эффективности по k-го вида основных производственных фондов;
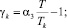
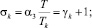
θk = T/Tk;
γ = (1 – α3)(1 – β) (k = 1, ..., n) .
Чистая прибыль (после налогообложения), полученная участниками агропродовольственного кластера, будет описана следующим выражением:
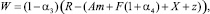(1)
где α3 – ставка единого сельскохозяйственного налога (ЕСХН); α4 – ставка отчислений с фонда оплаты труда на обязательное страхование, или, с учетом введенных обозначений,
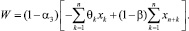(2)
Собственные средства агропродовольственного кластера можно представить в виде: Ds = Am + W или, с учетом введенных обозначений,
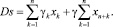(3)
Предположим, что в процессе своего функционирования агропродовольственный кластер будет платежеспособен, то есть выполняется условие Ds ≥ 0.
Среди основных факторов, влияющих на стабильность развития и эффективность функционирования любой экономической системы, можно выделить два фактора. Первый – фактор спроса на производимую продукцию как основной рыночный фактор, позволяющий избежать неэффективного развития экономической системы из-за перепроизводства продукции. Второй – фактор научно-технического прогресса, ограничивающего производственные возможности экономической системы характеристиками и уровнем развития основных фондов, которые непосредственно вовлечены в процесс производства продукции и влияют на объем и качество выпускаемой продукции. Поэтому при функционировании агропродовольственного кластера целесообразно рассматривать следующие ограничения:
1) 0 ≤ Pkmkyk ≤ qk – объем продаж продукции k-го типа (в стоимостном выражении) не превышает спрос на нее;
2) 0 ≤ yk(t) ≤ qk, то есть выпуск продукции k-го типа не превосходит производительности ОПФ (определяемой уровнем научно-технического прогресса).
Критерием эффективности (оптимизации) в модели агропродовольственного кластера будем считать его чистую приведенную стоимость J, отражающую добавленную стоимость функционирования создаваемой интегрированной структуры:
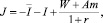(4)
где r – ставка дисконтирования, учитывающая уровень инфляции, требования доходности инвестора и другие риски за весь период функционирования агропродовольственного кластера.
Таким образом, можно говорить об универсальности приведенной оптимизационной математической модели для оценки эффективности агропродовольственного кластера, в которой учтены операционные, инвестиционные, финансовые потоки, возникающие в результате деятельности участвующих в данной социально-экономической системе экономических агентов – производителя (прибыль, затраты), потребителя (фонд оплаты труда), налогового органа (крупнейшие налоговые потоки), а также ограничения их деятельности (платежеспособность, спрос, научно-технический прогресс, инвестиционные ограничения) – с учетом специфики сельскохозяйственного производства региона.
Учитывая введенные обозначения и формулы (1)–(4), математическая модель агропродовольственного кластера приобретет формализованный вид:
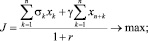(5)
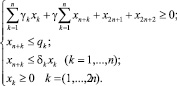
Заключение
Модель (5) является многопараметрической задачей линейного программирования, при решении которой определяется оптимальный уровень инвестиций, производства и выручки от реализации продукции. В ней учитываются налоговые потоки, зарплатоемкость, материальные затраты, характеристики основных производственных фондов (среднегодовая стоимость, срок полезного использования), характеристики продукции (стоимость по каждому виду сельскохозяйственной продукции, потребительский спрос), показатели среды функционирования агропродовольственного кластера (показатели внутренней и внешней среды): ставка дисконтирования (учитывающая уровень инфляции, требования доходности инвестора и другие риски за весь период функционирования агропродовольственного кластера), горизонт планирования, максимальные суммы инвестиционных вложений в развитие отрасли.
В отличие от базовой модели, приведенная здесь модель адаптирована к анализу функционирования регионального агропродовольственного кластера и имеет следующие содержательные особенности.
- Модель впервые применяется к агропродовольственному кластеру, который характеризуется высокой материальной затратностью сельскохозяйственного производства (удельный вес материальных затрат в структуре затрат на производство сельскохозяйственной продукции колеблется на уровне 60–70 %).
- Может учитывать специфику сельскохозяйственного производства в виде высокой зарплатоемкости (удельного веса заработной платы работников отрасли в общих затратах агропредприятий), что ведет к низкой производительности труда и ограничивает конкурентоспособность отрасли.
- Может учитывать повышенный срок эксплуатации основных производственных фондов в АПК, существенно отличающийся от других отраслей экономики. Более 80 % техники и оборудования в сельском хозяйстве, используемых в производственном процессе, находятся за пределами нормативного срока эксплуатации.
- Допускает возможность применения специального режима налогообложения – единого сельскохозяйственного налога (ЕСХН) для сельскохозяйственных предприятий, существенно снижающего налоговую нагрузку на сельскохозяйственных товаропроизводителей и первичных переработчиков сельскохозяйственного сырья.
- Учитывает особенности динамики спроса на продукцию, характеризующегося относительным постоянством, что отличает сельскохозяйственную отрасль от других отраслей экономики.
Модель (5) может быть положена в основу определения прогнозного экономического эффекта от функционирования агропромышленного кластера.
Рецензенты:
Попов Е.А., д.ф.-м.н., профессор кафедры системного анализа и исследования операций Сибирского государственного аэрокосмического университета имени академика М.Ф. Решетнева, г. Красноярск;
Березнев С.В., д.э.н., профессор, ФГБОУ ВПО «Кузбасский государственный технический университет имени Т.Ф. Горбачева», г. Кемерово.
Работа поступила в редакцию 30.10.2013.