Ведущей отраслью промышленного развития государства является машиностроение. В последние годы в Российской Федерации проблеме развития машиностроения уделяется особое внимание, поставлены задачи о его коренной модернизации на основе внедрения инновационных подходов. Решение этих важных задач возможно только при использовании результатов новейших научных исследований и, в первую очередь, в теории машин, одним из основных разделов которой является синтез структур механизмов, позволяющих решать поставленные практикой технологические задачи.
Настоящее исследование проводится с целью разработки основополагающих условий структурного синтеза механизмов, отнесенных академиком И.И.Артоболевским ко второму семейству [1], которые, имея перспективы широкого применения в технике, до настоящего времени оставались практически не исследованными.
Методы исследования основаны на принципах теории структурного синтеза кинематических цепей при использовании универсальной структурной системы; приемах конструирования деталей машин. Объектом исследования являются механизмы второго семейства, предметом исследования – их структура.
В течение ХХ века благодаря исследованиям Л.В. Ассура [2], А.П. Малышева [7], В.В. Добровольского [4], Н.И. Колчина [6], И.И. Артоболевского [1], С.Н. Кожевникова [5], О.Г. Озола [8], Л.Н. Решетова [9] и других ученых теория структуры механизмов была развита до ее прямого использования в практике машиностроения.
Анализ трудов перечисленных исследователей показал, что к началу ХХI века были выявлены принципы построения кинематических цепей, определены основы их классификации и разработаны методы их исследования.
Структурная формула плоских механизмов, выведенная П.Л. Чебышевым в 1869 г., имеющая вид [10]
W = 3n – 2p5, (1)
где W – подвижность цепи; n – число подвижных звеньев; р5 – число одноподвижных кинематических пар, была развита А.П. Малышевым в 1923 г. в формулу [7]
W = 6n – 5p5 – 4p4 – 3p3 – 2p2 – p1, (2)
для пространственных механизмов, где р5, р4, р3, р2 и р1 – одно-, двух-, трех-, четырех- и пятиподвижные кинематические пары, а в 1939 году В.В. Добровольским была выведена универсальная структурная формула для всего многообразия механизмов в виде [4]
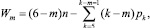 (3)
(3)
где m – число общих связей, накладываемых на механизм.
Последняя формула позволила И.И. Артоболевскому впервые обосновать классификацию механизмов по семействам в зависимости от параметра m, который может принимать значения 0, 1, 2, 3 или 4 [1]. Для механизмов нулевого семейства m = 0 и формула (3) для них полностью повторяет формулу (2) А.П. Малышева. При m = 1 организуются механизмы первого семейства, структурная формула которых выглядит следующим образом:
W1 = 5n – 4p5 – 3p4 – 2p3 – p2. (4)
Для механизмов второго семейства параметр m принимается равным двум (m = 2), и их формула подвижности записывается как
W2 = 4n – 3p5 – 2p4 – p3. (5)
Движение звеньев механизмов третьего семейства ограничивается тремя общими наложенными связями (m = 3)
W3 = 3n – 2p5 – p4. (6)
На движение звеньев механизмов четвертого семейства накладываются четыре общие связи (m = 4). Их формула подвижности определяется формулой В.В. Добровольского
W4 = 2n – p5. (7)
К настоящему времени в большей или меньшей степени исследованными и широко используемыми в практике являются простейшие механизмы нулевого семейства, плоские и сферические механизмы третьего семейства, клиновые и винтовые механизмы четвертого семейства. Что же касается механизмов первого и второго семейств, то они фактически являются неисследованными. Так, все сведения о механизмах второго семейства, содержащиеся в работах В.В. Добровольского и И.И. Артоболевского, касаются лишь нескольких кинематических схем, три из которых приведены на рис. 1.

Пространственный рычажно-винтовой механизм
Винто-рычажный механизм для перемещения коромысла
Пространственный рычажно-винтовой механизм
Рис. 1. Известные механизмы второго семейства
Опыт последних лет и анализ технических возможностей таких механизмов дает основания утверждать, что их практическое применение в технике может иметь весьма широкие перспективы.
Систематическое исследование строения (структуры) механизмов второго семейства было начато с установления возможных подсемейств механизмов, анализа пространств их функционирования и с рассмотрения полного состава кинематических пар, которые в таких механизмах могут быть применены.
Внутри второго семейства оказалось возможным выделить принципиально отличающиеся друг от друга подсемейства механизмов в зависимости от того, какие по классам кинематические пары в них используются. С учетом формулы (5) в механизмах второго семейства могут использоваться пары только трех классов – пятого (р5), четвертого (р4) и третьего (р3). Поэтому всего во втором семействе было выделено семь подсемейств. Структурно они описываются формулами
1) W2(1) = 4n – 3p5 – 2p4 – p3
2) W2(2) = 4n – 3p5 – 2p4
3) W2(3) = 4n – 3p5 – p3
4) W2(4) = 4n – 3p5
6) W2(6) = 4n – 2p4
7) W2(7) = 4n – p3
5) W2(5) = 4n – 2p4 – p3
Обязательным условием для всех семи подсемейств является наличие ненулевых значений чисел кинематических пар в правых частях их уравнений. Из приведенных формул подсемейств видно, что они описывают принципиально разные структуры, которые требуют своих подходов к их построению и дальнейшему исследованию.
Механизмы второго семейства, как и всех других семейств, могут создаваться в различных пространствах функционирования. В полном декартовом пространстве – ВПВПВП (вращательное В и поступательное П движения относительно всех трех осей координат) могут иметь движения лишь звенья механизмов нулевого семейства, описываемых формулой (2) А.П. Малышева и являющихся самоустанавливающимися.
Так как на движения звеньев механизмов второго семейства накладываются два общих условия связи (m = 2), которые могут быть различными, а именно в виде ПП, ПВ, ВВ или ВП, то пространствами функционирования таких механизмов могут быть следующие четыре ВПВВ, ВППВ, ВППП и ВПВП, которые показаны на рис. 2.

Пространство ВПВВ
Пространство ВППВ
Пространство ВППП
Пространство ВПВП
Рис. 2. Пространства функционирования механизмов второго семейства
Отметим, что в каждом из показанных пространств присутствуют движения ВП – вращательное В и поступательное П движения относительно одной из координатных осей. Третьим и четвертым относительным движением являются ВВ, ПВ или ПП относительно других осей и ВП относительно второй оси. Очевидно, что механизмы, построенные в четырех показанных пространствах, имеют также принципиальные отличия друг от друга не только по структуре, но и по методам их исследования.
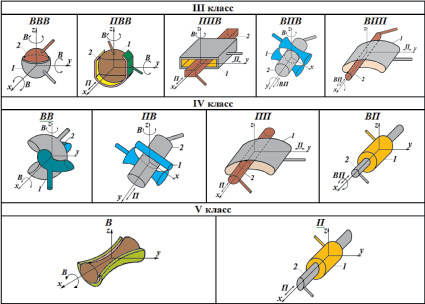
Помимо отмеченного выше, кинематические пары пятого, четвертого и третьего классов, используемые в механизмах второго семейства, отличаются по составу относительных движений в них. Так, кинематические пары третьего класса могут обеспечивать пять комплексов относительных движений (ВВВ, ПВВ, ППВ, ВПВ и ВПП), четвертого класса – четыре (ВВ, ПВ, ПП и ВП) и пятого – два (В и П). Специально выполненное исследование позволило выявить все возможные из перечисленных пар, которые впервые полностью приведены в таблице. При этом пары выполнены удерживающими (двухстороннего действия).
Следующим отличием структур механизмов является деление их на виды в зависимости от параметра τ универсальной структурной системы профессора Л.Т. Дворникова [3]
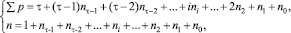 (8)
(8)
который определяет сложность базисного звена цепи – от двухпарного (τ = 2), трехпарного (τ = 3) и т.д. до наиболее сложного. В (8) под ni понимается число звеньев, добавляющих в цепь по i кинематических пар.
Внутри видов механизмы могут различаться по подвидам в зависимости от используемых звеньев ni. Например, III вид механизмов (τ = 3) содержит два подвида, описываемые формулами:
1) p5 + p4 + p3 = 3 + 2n2 + n1;
2) p5 + p4 + p3 = 3 + n1.
Полный состав удерживающих кинематических пар III, IV и V классов
Разработанные критерии структурного синтеза позволяют создавать любые по сложности механизмы второго семейства. Обратимся к частной задаче создания механизма (W = 1) с четырьмя подвижными звеньями (n = 4), в котором одновременно будут присутствовать кинематические пары пятого р5, четвертого р4 и третьего р3 классов (первое подсемейство), наиболее сложным звеном будет трехпарное – τ = 3 (III вид), остальные звенья будут добавлять по одной кинематической паре каждое – n1 (второй подвид).
Запишем универсальную структурную систему (8) совместно с формулой подвижности первого подсемейства при заданных параметрах
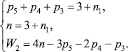
Выразим n1 из второго уравнения системы и введем его в первое уравнение. С учетом n = 4 преобразуем исходную систему к виду
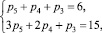
откуда путем исключения параметра р5 получим уравнение р4 + 2р3 = 3, которое имеет единственное решение: р4 = 1, р3 = 1. Тогда из исходной системы определим, что р5 = 4, а n1 = 3. Запишем полное решение в виде: W2 = 1, τ = 3, n = 4, n1 = 3, р5 = 4, р4 = 1, р3 = 1.
По найденному решению покажем на рис. 3 кинематическую схему механизма с виртуальными парами, а на рис. 4 – с реальными парами.
Под виртуальной парой в данном случае понимается пара, на место которой может быть поставлена пара III, IV или V классов согласно полученному решению. Далее на место кинематической пары определенного класса будет введена выбранная пара с конкретным комплексом движений. Например, если это пара третьего класса, то на место виртуальной пары может быть поставлена ВВВ, ПВВ, ППВ, ВПВ или ВПП. Такой подход позволяет найти все без исключения схемы механизмов при заданных параметрах.
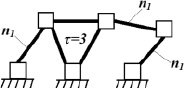
Рис. 3. Схема пятизвенного механизма с виртуальными парами
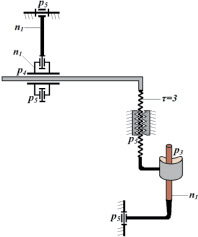
Рис. 4. Схема пятизвенного механизма с реальными парами
Подвижность пятизвенного механизма определится по формуле (5) как
W2(1) = 4n – 3p5 – 2p4 – p3 = = 4∙4 – 3∙4 – 2∙1 – 1 = 1,
то есть механизм обладает одной степенью свободы и в нем достаточно задать движение одному звену, чтобы все остальные звенья двигались вполне определенно.
Заключение
Таким образом, полный системный синтез структур механизмов второго семейства возможен при условии четкого разделения их на семь подсемейств, изучения их функционирования в четырех различных пространствах, разделении их на виды и подвиды в зависимости от сложности базисного звена и при учете всего многообразия кинематических пар третьего, четвертого и пятого классов.
Работа выполнена при финансовой поддержке в форме гранта DAAD и Министерства образования и науки Российской Федерации по программе «Михаил Ломоносов» (регистрационный № 11.7190.2013).
Рецензенты:
Притыкин Ф.Н., д.т.н., профессор кафедры «Инженерная геометрия и САПР», ФГБОУ ВПО «Омский государственный технический университет», г. Омск;
Живаго Э.Я., д.т.н., профессор, заведующий кафедрой теоретической механики, ФГБОУ ВПО «Сибирский государственный индустриальный университет», г. Новокузнецк.
Работа поступила в редакцию 29.10.2013.



