При проектировании глубоководных нефте- и газопроводов, подводных трубопроводов и насосов, применяемых при добыче нефти с морских платформ, а также в других устройствах, связанных с транспортировкой жидкости на значительные расстояния, весьма актуальным является вопрос о недопущении передачи шума и вибрации по трубопроводу от их источника на значительные расстояния. Такая передача связана с зарождением распространяющейся волны, которая появляется на некоторых частотах. Современный тонкостенный трубопровод представляет собой тонкую цилиндрическую оболочку, поэтому вопрос об определении её волновых чисел и построении дисперсионных кривых весьма актуален. Этот вопрос рассматривался различными авторами монографий и статей в разное время (см., например, [2, 5]) с применением различных теорий оболочек (моментной и различных упрощенных теорий), но недостаточно внимания уделялось сопоставлению результатов и определению границ применимости различных теорий для удовлетворения практических потребностей при проектировании. Поэтому возникла необходимость расчета всех вещественных, мнимых и полностью комплексных волновых чисел на основе моментной теории, построения дисперсионных кривых и сопоставления полученных результатов с теми, которые получаются по упрощенным теориям.
Рассматривается бесконечная цилиндрическая оболочка толщины h с радиусом срединной поверхности R
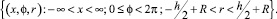
Уравнения движения такой оболочки по моментной теории (см. [3]) запишутся:
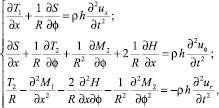 (1)
(1)
где T1, T2, S – осевое, окружное и поперечное усилия; M1, M2, H –продольный изгибающий, окружной изгибающий и крутящий моменты соответственно.
Переходя к перемещениям и опираясь на работу [4], получаем следующую систему уравнений, описывающую свободные колебания такой оболочки:
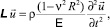 (2)
(2)
где матрица оператора
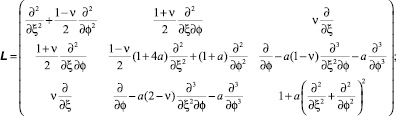
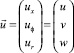 – вектор перемещения; ρ – плотность; Е – модуль Юнга; ν – коэффициент Пуассона;
– вектор перемещения; ρ – плотность; Е – модуль Юнга; ν – коэффициент Пуассона; 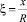 – безразмерная осевая координата,
– безразмерная осевая координата, 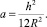
Введем, для компактности записи, обозначения k = λR и 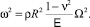 Будем называть k и m осевым и окружным волновыми числами соответственно, а ω – частотой (на самом деле это приведенный параметр частоты).
Будем называть k и m осевым и окружным волновыми числами соответственно, а ω – частотой (на самом деле это приведенный параметр частоты).
Перенесем инерционные члены налево и будем искать решения системы (2) в виде
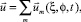 (3)
(3)
где 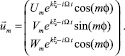
Это позволит искать решения отдельно для каждого m. Тогда получим систему вида
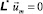 (4)
(4)
с матрицей оператора
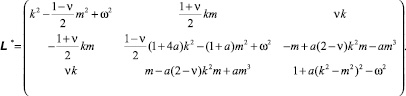
При рассмотрении задачи по безмоментной теории следует в матрицах (2) и (4) положить a = 0. При использовании упрощенной теории Власова (см. [1] и [3]), которая, вообще говоря, применяется для коротких оболочек, следует положить a = 0 во всех элементах матрицы, кроме L33 и, соответственно 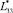 . Если же применять полумоментную (или полубезмоментную) теорию, пренебрегая в уравнениях движения окружным изгибающим и крутящим моментами (см. [3]), то матрица запишется:
. Если же применять полумоментную (или полубезмоментную) теорию, пренебрегая в уравнениях движения окружным изгибающим и крутящим моментами (см. [3]), то матрица запишется:
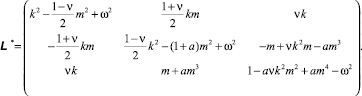 (5)
(5)
Для удобства введем новые обозначения для коэффициентов при различных степенях k. Тогда матрица запишется:
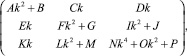 (6)
(6)
где
A = 1; 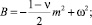
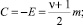 D = K = ν;
D = K = ν;
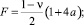
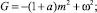
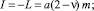

N = a; 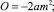
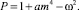
По безмоментной теории следует положить a = 0 во всех коэффициентах матрицы (6). По упрощенной теории Власова следует положить a = 0 во всех коэффициентах, кроме N, O, P. При использовании полумоментной теории следует в (6) принять 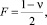 I = aνm, L = 0, N = 0; O = –aνm2, а остальные коэффициенты оставить без изменения.
I = aνm, L = 0, N = 0; O = –aνm2, а остальные коэффициенты оставить без изменения.
Приравнивая к нулю определитель этой матрицы, приходим к одному из следующих уравнений для k:
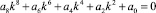 (для моментной и упрощенной теорий),
(для моментной и упрощенной теорий),
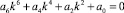 (для полумоментной теории), (7)
(для полумоментной теории), (7)
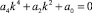 (для безмоментной теории).
(для безмоментной теории).
В случае m = 0 для полумоментной теории уравнение (7) будет четвёртого порядка. Коэффициенты этих уравнений очевидным образом выражаются из (6).
Ниже представлены результаты расчетов корней этих уравнений при ν = 0,3 в среде Mathcad. При определении корней уравнений (7) значения окружного волнового числа m фиксировались равными 0, 1, 2, 3. Соотношение 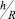 принималось равным 0,025. Искались все возможные вещественные и комплексные значения осевого волнового числа k в зависимости от частоты ω. Корни уравнений (7) могут быть либо полностью комплексные вида
принималось равным 0,025. Искались все возможные вещественные и комплексные значения осевого волнового числа k в зависимости от частоты ω. Корни уравнений (7) могут быть либо полностью комплексные вида 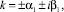 либо вещественные вида
либо вещественные вида 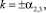 либо чисто мнимые вида
либо чисто мнимые вида 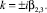 Поэтому на рисунках приводятся значения корней только со знаком «+» у вещественной и мнимой частей. Полностью комплексные корни изображены сплошной линией, а чисто вещественные и чисто мнимые – пунктирной.
Поэтому на рисунках приводятся значения корней только со знаком «+» у вещественной и мнимой частей. Полностью комплексные корни изображены сплошной линией, а чисто вещественные и чисто мнимые – пунктирной.
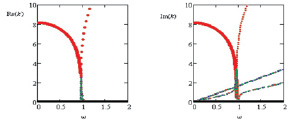
Рис. 1. Дисперсионные кривые при m = 0 (осесимметричные колебания). Красные – по моментной теории и теории Власова (совпадают), синие – по полумоментной теории, зеленые – по безмоментной теории
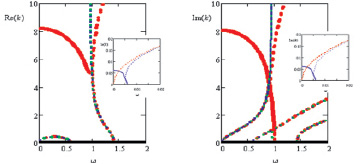
Рис. 2. Дисперсионные кривые при m = 1 (балочные колебания). Красные – по моментной теории и теории Власова (совпадают), синие – по полумоментной теории, зеленые – по безмоментной теории. На вставках при малых частотах: красные – по моментной, полумоментной и безмоментной теориям (совпадают), фиолетовые – по теории Власова
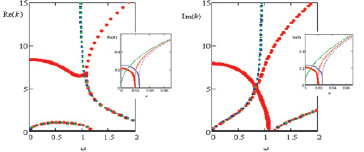
Рис. 3. Дисперсионные кривые при m = 2 (неосесимметричные колебания, две волны в поперечном сечении). Красные – по моментной теории и теории Власова (совпадают), синие – по полумоментной теории, зеленые – по безмоментной теории. На вставках при малых частотах: красные – по моментной и полумоментной теориям (совпадают), фиолетовые – по теории Власова, зеленые – по безмоментной теории
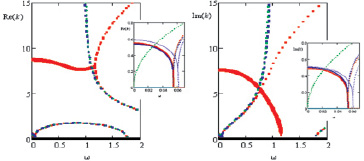
Рис. 4. Дисперсионные кривые при m = 3 (неосесимметричные колебания, три волны в поперечном сечении). Красные – по моментной теории и теории Власова (совпадают), синие – по полумоментной теории, зеленые – по безмоментной теории. На вставках при малых частотах: красные – по моментной теории, синие – по полумоментной, фиолетовые – по теории Власова, зеленые – по безмоментной теории
Анализ рис. 1–4 показывает, что безмоментная теория не позволяет определить комплексные ветви дисперсионных кривых, которые соответствуют затухающим волнам, для всех рассмотренных m. Первая распространяющаяся волна (чисто мнимые k) по безмоментной теории всегда появляется при ω = 0, что согласуется с моментной только при m = 0 и m = 1. Безмоментная теория перестаёт улавливать первую распространяющуюся волну, начиная с ω ≈ 0,9во всех случаях. Из двух вещественных ветвей, на которые распадается комплексная при ω ≥ 1, безмоментная теория определяет только нижнюю. Полумоментная теория, как и безмоментная, не позволяет найти комплексные ветви и точки бифуркации, но точно определяет частоты отсечки распространяющихся волн. Моментная теория и теория Власова дают близкие результаты, кроме случая m = 1 (см. вставку в рис. 2), когда теория Власова дает несуществующую по другим теориям комплексную ветвь, начинающуюся с ω = 0, а первая распространяющаяся волна появляется при чуть больших ω. На малых частотах при m = 2 и m = 3 (см. вставки в рис. 3 и 4) преимущество имеет полумоментная теория, результаты которой почти полностью совпадают с моментной. Теория Власова при этом дает на малых частотах незначительные отличия от моментной.
С физической точки зрения представляется достаточно очевидным, что безмоментная теория, при которой в уравнениях движения пренебрегают всеми моментами, не даёт реального значения частоты отсечки первой распространяющейся волны в режиме изгибных колебаний и неосесимметричных режимах, а применима только для осесимметричного (мембранного) режима m = 0.
Вышеизложенное позволяет сделать вывод, что для определения частот отсечки на не слишком малых частотах (ω > 0,07) можно использовать любую упрощенную теорию, ибо каждая из них позволяет точно определить частоты отсечки, что особенно важно для определения диапазона частот, в котором осевые волновые числа чисто мнимые, и соответственно имеется распространяющаяся волна. На малых частотах следует использовать только полумоментную или моментную теории. Следует иметь в виду, что по безмоментной и полумоментной теориям можно лишь косвенно судить о диапазонах частот, в которых имеют место затухающие волны, ибо эти теории не позволяют найти полностью комплексные корни. Если эти сведения необходимы, то наилучшие результаты дает теория Власова. Кроме вышеизложенного, исследовалась возможность применения к рассматриваемой задаче теории пологих оболочек Власова [1], когда в уравнениях движения пренебрегают продольным изгибающим моментом по сравнению с окружным. Эта теория позволяет успешно определять комплексные ветви дисперсионных кривых и частоты отсечки, но при малых ω, кроме ветвей, согласующихся с моментной теорией, даёт еще дополнительные. Отметим также, что в работе [6] предлагается находить отдельно большие и малые по модулю k, принимая во внимание, что коэффициенты a8 и a6 в уравнении (7) имеют существенно меньший порядок по сравнению с остальными, что приводит к тем же результатам, что и безмоментная теория.
Рецензенты:
Сорокин С.В., д.т.н., профессор кафедры сопротивления материалов Санкт-Петербургского государственного морского технического университета, г. Санкт-Петербург;
Картузов Е.И., д.т.н., профессор кафедры теоретической механики Санкт-Петербургского государственного морского технического университета, г. Санкт-Петербург.
Работа поступила в редакцию 30.10.2013.



