Долгосрочный прогноз в экономике является актуальной задачей на протяжении всего времени её существования. В связи с этим решению данной задачи посвящено множество работ как российских, так и зарубежных авторов [5]. Один из популярных подходов основан на так называемой теории предвидения, выдвинутой ещё Н.Д. Кондратьевым [6] и впоследствии развитой многими его последователями. Существующая также теория макропрогнозирования сочетает в себе достоинства теории предвидения и теории циклов, кризисов и инноваций Н.Д. Кондратьева, учение о ноосфере и цивилизационный подход Н.Н. Моисеева и В.И. Вернадского и балансовый метод В.В. Леонтьева.
На сегодняшний день активно развиваются методы прогнозирования на основе нелинейной динамики, теории фракталов и математической статистики – фундаментальных математических дисциплин. Одним из наиболее интересных направлений в разработке методов анализа и прогнозирования экономических систем, по мнению авторов, является метод Хёрста, или R/S метод, получивший также название метода нормированного размаха. Данный эмпирический метод был предложен для статистического анализа временных рядов ещё в начале XX века Хёрстом [8] и основан на результатах его наблюдений за развитием многих природных процессов, Например, количество осадков, сток рек, толщина годовых колец на деревьях, донных отложений и пр. Длительное измерение эволюции множества природных показателей обнаруживает их, на первый взгляд, беспорядочное поведение, как на коротких, так и на длинных временных интервалах. Для анализа временных последовательностей исследуемых величин и существует метод, разработанный Хёрстом.
Классический метод Хёрста. Для исследуемого временного ряда ξ(t) вводится среднее значение <ξ(t)> на интервале времени τ, затем рассчитывается зависимость накопленного отклонения X(t, τ) на интервале времени τ, по которому вычисляется функция абсолютного размаха R:
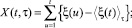
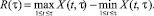
Далее вычисляется зависимость безразмерной функции R/S от длины временного интервала τ делением R на стандартное отклонение S(τ) ряда ξ(t). По результатам исследования многих природных процессов Хёрстом была установлена эмпирическая связь между нормированным размахом R/S и длиной интервала τ через показатель H [7]:
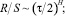
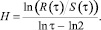 (1)
(1)
Впоследствии самим Хёрстом было доказано, что Н может принимать значения от 0 до 1. Для анализа экономических показателей, порождённых определённой экономической системой, это имеет следующий смысл. В случае отсутствия долговременной статистической зависимости (случайное поведение экономического показателя), данное отношение должно асимптотически стремиться к τ1/2 (Н = 0,5) при стремлении длины выборки к бесконечности, что на примере броуновского движения было доказано ещё Б. Мандельбротом. Значения же Н > 0,5 характеризуют сохранение тенденций к росту или убыванию показателя, как в прошлом, так и в будущем (персистентное поведение – сохранение структуры) [7]. Н < 0,5 означает склонность экономической системы к постоянной смене тенденции: рост сменяется убыванием и наоборот. В работах [1,2] было установлено, что все эти свойства справедливы даже для относительно коротких временных рядов.
Модернизированный метод Хёрста. Время достоверного прогноза. В работах [1, 2] было показано, что если сделать предположение о зависимости показателя H в выражении (1) от временного масштаба τ и определить функцию H(τ) из производной функции R/S по τ, то для удобства численного дифференцирования функции R/S в виде временного ряда выражение для нахождения зависимости H(τ) примет следующий вид:
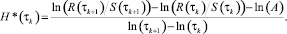 (2)
(2)
По поведению характеристической функции можно классифицировать временные ряды, как статистически фрактальные, случайные, периодические. Можно выделить ещё один тип с глобальной персисистентностью, который характерен для функций роста или убывания. По поведению этой функции в случае анализа существенно нелинейной экономической системы с хаотическим поведением можно установить характерное время выхода на случайный процесс. Это время, как показано в работе [3], близко ко времени забывания начальных условий, на котором теряется корреляция (взаимосвязь) будущих значений с прошлыми. Поэтому точное предсказание поведения исследуемой системы на интервалах времени, больших tr становится невозможным. Достоверное прогнозирование на интервалы времени, превышающие tr, невозможно, поэтому tr, можно назвать временем достоверного прогноза.
Следует отметить наличие сложной структуры в территориально-экономических отношениях. В геометрическом отношении эта структура является пространственно распределенной с широко развитым древом ветвлений, заканчивающихся на микротерритории домашнего хозяйства. Это подтверждает существование фракталов в экономике, как в территориальном, так и экономическом отношении. В экономике фрактал – это множество, подобное самому себе в территориально-экономическим смысле. Различного рода фрактальные структуры в экономических системах приводят к фрактальному поведению экономических показателей таких систем. Метод Хёрста, применяемый для анализа фрактальных свойств экономических систем по временным рядам начиная от экономики региона и заканчивая макроэкономикой, может применяться и для прогнозирования поведения таких систем.
Учёт изменения управляющих параметров в прогнозировании
Считая фрактальные свойства территориально-экономической системы неизменными (постоянство территории и неизменность для них соотношений потоков товаров и капитала, а главное – форм собственности) возможно достроение временного ряда исследуемого экономического показателя на некоторый временной интервал в будущем. Если фрактальные свойства территориально-экономической системы не изменятся за время прогнозирования, то появляется возможность точно предсказать её поведение на таком участке времени. Функция R/S и показатель Хёрста в этом случае считаются постоянными для системы с неизменными фрактальными свойствами и не зависящими от длины исследуемого временного ряда. Поэтому достроение временного ряда на некоторый интервал в будущем выполняется таким образом, чтобы оно не меняло функцию Хёрста для исследуемого ряда. Подробнее это описано в работах [1,2].
Однако нельзя быть уверенным, особенно при использовании для прогнозирования временных рядов экономических показателей за достаточно длительный промежуток времени, что за это время не произошло никаких изменений основных управляющих параметров нелинейной территориально-экономической системы, следовательно, и её фрактальных свойств. Особенно этот вопрос касается макроэкономических показателей, вклад в которые дают множество отдельных территориально-экономических единиц. В этом случае необходимо оценивать достоверность такого прогнозирования, даже несмотря на автоматический учёт при построении прогноза времени забывания начальных условий.
Дело в том, что при изменении параметров даже четко детерминированных систем, например классической системы уравнений Лоренца, происходит неизбежно и изменение времени забывания начальных условий. Это означает, что в функцию R/S, рассчитываемую для прогнозирования хоть и по последним (ближайшим к прогнозируемой) точкам, однако же, с увеличением τ охватывающую всё больший временной интервал, дают вклад как последние значения временного ряда, так и довольно «давние». При наличии изменения параметров системы за этот интервал времени таким образом неизбежно находится некоторая усреднённая функция R/S и соответственно показатель Хёрста. Наличие такого усреднения негативно влияет на точность (следовательно, на общую достоверность) прогнозирования. Так как постоянное изменение параметров территориально-экономических систем неизбежно, необходимо оценивать степень такого изменения для коррекции метода с целью повышения достоверности прогнозирования даже на временных интервалах, не превышающих времени забывания начальных условий.
Такая коррекция возможна, если знать, на каком участке исходного для прогнозирования временного ряда изменение параметров не превысило некоторую допустимую для данной конкретной ситуации построения прогноза норму. Оказывается, оценить это изменение можно по ширине «коридора» изменения функции R/S, построенной, как выполнено в работах [1, 2], по скорости изменения исследуемого показателя (рис. 1). Если среднее значение функции R/S близко к обеим границам коридора, по сравнению с её текущим значением, то, следовательно, влияющие параметры системы за анализируемый промежуток времени менялись незначительно.
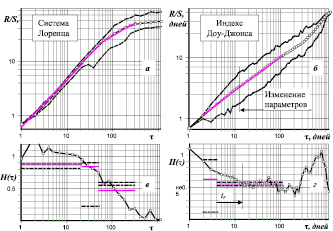
Рис. 1. Изменение функции нормированного размаха и соответствующая её зависимость показателя Хёрста от временного интервала для системы уравнений Лоренца (а, в) и для индекса Доу-Джонса (б, г) за 2005–2011 гг. соответственно. Пунктирной и штрихпунктирной линиями выделен коридор изменения функции R/S. Светлой сплошной линией показано усреднение показателя Хёрста на участке 1–20, 20–40 и 40–250 для системы уравнений Лоренца и 2–5, 5–100 дней для индекса Доу-Джонса. Пунктирной и штрихпунктирной линией на в, г) обозначены усреднённые значения Н для верхней и нижней границы функции R/S
Оценка «коридора» изменения функции R/S проводилась следующим образом. Вычислялся весь спектр значений R(τ)/S(τ) по всему временному ряду при условии, что τ < t0, где t0 – длина временного ряда. Для дискретного набора N выборок, которым является временной ряд, это возможно, если определить τ’ = τ/h, t′ = t/h, где h = t0/N – временной шаг. В этом случае дискретная функция накопленного отклонения Xt′,τ′,i и функция размаха Rt′,τ′,i могут быть представлены в виде:
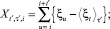
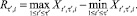
Тогда максимальным и минимальным значением R/S или верхней и нижней границей коридора можно называть величины:
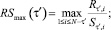
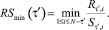
Если среднее значение функции R/S близко к обеим границам коридора, по сравнению с её текущим значением, то, следовательно, влияющие параметры системы за анализируемый промежуток времени менялись незначительно. Если среднее значение функции R/S остаётся близким к верхней границе, при этом нижняя испытывает резкий «скачок» в сторону уменьшения – это означает приближение и переход через время забывания начальных условий. На рис. 1, а, в приведён пример для системы уравнений Лоренца с неизменными параметрами. Анализ проводился по первой производной первой переменной. Хорошо виден узкий коридор (рис. 1а) и соответствующие ему близкие значения показателя Хёрста для каждой функции R/S (рис. 1, в) на интервале 1–20 единиц приведённого времени. При переходе через время забывания начальных условий происходит резкий отрыв нижней границы функции R/S и, как следствие, резкое уменьшение соответствующего ей показателя Хёрста (штрихпунктирная линия на рис. 1, а,в интервал 20–40). При этом верхняя граница остаётся по прежнему близка к среднему значению функции R/S, что может являться характеристикой неизменности параметров такой системы.
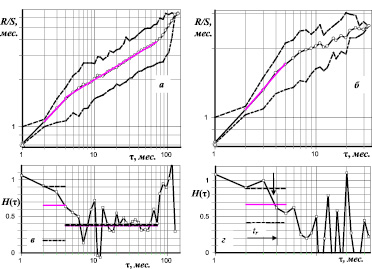
Рис. 2. Изменение функции нормированного размаха и соответствующая её зависимость показателя Хёрста от временного интервала для ИПП за период с 2000 по 2011 г. а, в) и за период с 2001 по 2007 г. б, г). Хорошо видна большая стабильность параметров региональной территориально-экономической системы в период с 2001 по 2007 г., нежели на всём периоде. Хорошо виден перепад показателя Хёрста (г) и выход его в область 0,5, что соответствует более точному определению времени забывания начальных условий на этом интервале
Для сравнения на рис. 1, б, г приведён R/S анализ с построением «коридора» для важного макроэкономического показателя и пока по прежнему непредсказуемого поведения индекса Доу-Джонса. Виден не только резкий отрыв нижней границы, что указывает на присутствие малых времён забывания начальных условий порядка нескольких дней, но также и отрыв верхней границы, что безусловно указывает на наличие периодических изменений параметров исследуемой макроэкономической системы «извне» в течение максимум каждых 10 дней. В таких условиях точно спрогнозировать поведение столь важного биржевого показателя при учёте постоянного изменения параметров порождающёй макроэкономической системы даже на несколько дней становится сложно, а на интервалы, превышающие 10 дней – невозможно. При этом среднее время достоверного прогноза остаётся на уровне 15–16 дней.
В качестве примера нахождения такого интервала на рис. 2 приведены результаты R/S анализа для ИПП. При анализе был определён интервал с 2000 по 2005 г., на котором основные параметры порождающей территориально-экономической системы изменялись гораздо слабее, чем за весь анализируемый период с 2000 по 2011 г. В качестве подтверждения на рис. 3б приведены два участка прогноза – первый для исходного ряда за 2001–2007 г. и второй – для участка 2000–2010 г.
Попытка соответствующего прогнозирования приведена на рис. 3, а. Хотя на интервале 8 дней можно считать прогноз достоверным, однако далее происходит разворот тренда, вызванный внешними силами, который не может быть предсказан, так как мы ничего не знаем о возможной эквивалентной математической модели и соответственно о величине воздействия на неё.
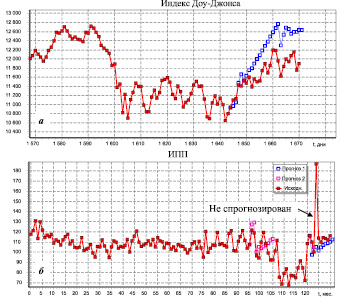
Рис. 3. Примеры построения прогноза с проверкой для исходного временного ряда индекса Доу-Джонса за период с 2005 по 2011 г. (а) и ИПП за период с 2000 по 2011 г. (б). На б) приведены прогнозные участки, соответствующие рис. 2, б, г – первый и рис. 2, а, в – второй
Однако же, в случае, если может быть установлен интервал, на котором параметры системы почти не изменялись, возможно прогнозирование с неплохой достоверностью, которое однако же не может превышать времени забывания начальных условий. При этом преимуществом определения такого интервала является более точная оценка самого времени забывания начальных условий.
По результатам прогнозирования хорошо видно, что его достоверность снижается при сильном изменении параметров системы, отражающегося в наличии широкого коридора функции R/S.
Заключение
Таким образом, метод Хёрста является неплохим методом для прогнозирования, так как позволяет сразу оценить время достоверного прогнозирования по наименьшей из величин: либо по времени забывания начальных условий, либо по периоду времени изменения параметров территориально-экономической системы, а также найти для прогнозирования участок исходного ряда с наибольшей стабильностью управляющих параметров. Возможность учёта изменения управляющих параметров, по мнению авторов, является большим его достоинством по сравнению с другими методами прогнозирования, особенно это касается линейных методов.
Все вычисления были выполнены с помощью специализированного программного продукта [4], модернизированного для решения поставленной в этой статье задачи.
Исследование выполнено при финансовой поддержке РГНФ в рамках научно-исследовательского проекта «Нелинейная динамика развития социально-экономических систем: диагностика, моделирование, прогнозирование», проект РГНФ № 11-02-00531а.
Рецензенты:
Быстрай Г.П., д.ф.-м.н., профессор кафедры общей и молекулярной физики Института естественных наук Уральского федерального университета, г. Екатеринбург;
Куклин А.А., д.э.н., профессор, руководитель центра экономической безопасности Института Экономики УрО РАН, г. Екатеринбург.
Работа поступила в редакцию 08.10.2013.



