Распространение поверхностных волн в слое жидкости на пористом основании рассмотрено в работах [8, 9]. Исследование математической модели распространения волн на поверхности слоя электропроводной жидкости с поверхностным электрическим зарядом, находящейся на слое пористой среды, проведено в [7]. Классическая задача о волнах на поверхности струи жидкости впервые была решена Релеем [1]. Волны на заряженной поверхности струи жидкости исследованы в [11]. Задача о волнах на поверхности струи магнитной жидкости рассмотрена в [10]. Задача о распространении волн на заряженной поверхности цилиндрического столба электропроводной жидкости, окружающей длинное пористое ядро, решена в [5] для случая электрода достаточно большого радиуса.
Предполагается, что внутри цилиндрического объема электропроводной несжимаемой жидкости находится ядро из пористого материала в форме коаксиально расположенного круглого цилиндра. Влиянием окружающего воздуха на распространение волн пренебрегается. Учитывается наличие поверхностного натяжения. Сила тяжести отсутствует. Ось пористого цилиндра направлена по оси коаксиального цилиндрического конденсатора, к электродам которого приложена разность потенциалов V. В качестве внутреннего электрода конденсатора используется поверхность проводящей жидкости. Задача решается в цилиндрической системе координат (r, θ, z), в которой жидкий столб покоится. Ось z направлена по оси пористого цилиндра. Радиус пористого цилиндра, невозмущенной поверхности жидкости и внешнего электрода обозначим a, a0 и b соответственно. Предположение о том, что величина b достаточно велика, далее не делается. Заряд будет сосредоточен на поверхности электропроводной жидкости [4]. Внутри жидкости и пористой среды напряженность электрического поля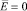 
и будет отлична от нуля в промежутке между электродами. На поверхности проводника выполняется соотношение
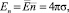
где 
– единичная внешняя нормаль к поверхности; σ – плотность поверхностного заряда. Величины, относящиеся к пористой среде и свободной жидкости, в необходимых случаях обозначаются индексами 1 и 2 соответственно.
Уравнения движения электропроводной жидкости в пористой среде при условии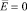 
имеют вид [9]:
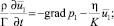
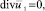(1)
где ρ – плотность жидкости; Γ – пористость (отношение объема пор ко всему элементарному объему среды); η – вязкость; K – коэффициент проницаемости пористой среды; p1 – давление;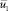 
– макроскопическая скорость фильтрации, связанная со средней скоростью v1 жидкости в порах соотношением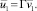 
Уравнения движения свободной жидкости при и в предположении, что амплитуда волны значительно меньше ее длины [3], запишем в линейном приближении
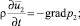
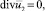(2)
где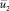 
– скорость свободной жидкости. Ограничиваемся случаем волн достаточно большой длины λ, существенно превышающей радиус a0 жидкого столба, с тем, чтобы пренебречь слагаемыми, содержащим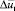и 
и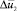 
в уравнениях (1) и (2).
Уравнения для электрического поля в воздухе [4]
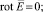
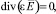(3)
где ε = const – диэлектрическая проницаемость.
Из уравнений (1)–(3) следует
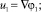
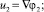
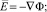(4)
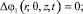
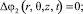
ΔΦ(r, θ, z, t) = 0.
Потенциал Φ запишем в виде
Φ = Φ0(r) + Φw(r, θ, z, t),
где Φw – малое возмущение, связанное с волной; Φ0 – невозмущенный потенциал, который находится из уравнения ΔΦ0 = 0 с граничными условиями Φ0(a0) = V, Φ0(b) = 0, и имеет вид:
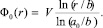
Справедливы равенства
E0(a0) = 4πσ0, (5)
где E0(r) – невозмущенное поле. Возмущенное поле записываем в виде
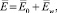
где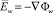 
и ΔΦw = 0.
Система граничных условий имеет вид:
на поверхности пористой среды (r = a)
1) u1r = u2r;
2) p1 = p2; (6)
на свободной поверхности жидкости (r = a0 + ξ(θ, z, t))
3) 
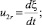
4) Φ0(a0 + ξ) + Φw = V = const;
5) 
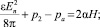
на внешнем электроде (r = b)
6) Φw(b) = 0.
Здесь pa – атмосферное давление; α – коэффициент поверхностного натяжения; H – средняя кривизна поверхности,
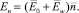
Давления запишем в виде
p1 = p10 + p1w, p2 = p20 + p2w,
где p10, p20 – равновесные давления.
В равновесии выполняются граничные условия
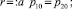
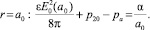(7)
Для возмущений давления из (1) и (2) следует
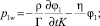
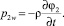(8)
С учетом выражений для 
и H [1]
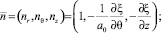
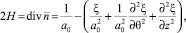
а также (4)–(8), линеаризованные граничные условия
1) 
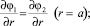(9)
2) 
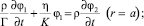
3) 
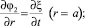
4) Φw – E0ξ = 0 (r = a);
5) 
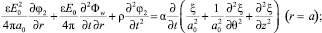
6) Φw(b) = 0.
Здесь E0 ≡ E0(a0), а также учтено, что
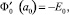
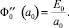
Математическая модель является, таким образом, краевой задачей, состоящей из уравнений Лапласа (4) и граничных условий (9).
Решение уравнений (4) с граничными условиями (9) ищем в виде
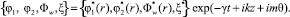
Здесь, например,
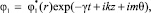
где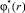 
– амплитуда; k = 2π/λ – волновое число; m = 0, 1, 2, …; γ = β + iω; ω – частота; β – коэффициент, который может быть как положительным (при затухании возмущения), так и отрицательным (при неустойчивости, приводящей к нарастанию возмущения).
Уравнение ∆φ1 = 0 принимает вид модифицированного уравнения Бесселя порядка m
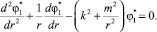
Общее решение этого уравнения
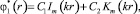
где Im и Km – модифицированные функции Бесселя первого и второго рода порядка m. Аналогично:
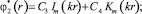
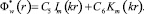
Следует положить C2 = 0, т.к. Km(kr) → ∞ при r → 0.
Граничные условия (9) для амплитуд
1) 
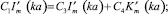(10)
2) 
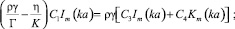
3) 
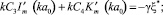
4) 
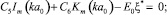
5) 
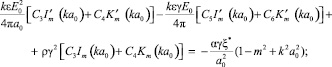
6) 
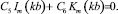
Из пяти равенств (исключая предпоследнее) (10) можно найти выражения коэффициентов C1, C3, C4, C5, C6 через величину ξ*, которую считаем малой первого порядка. В связи с рассмотрением длинных волн необходимо учесть физическое ограничение (k2K)/(Γ⟨⟨1), что приводит к ограничению интервала рассмотрения k (k ∈ [0; 2]). Подставляя найденные коэффициенты в предпоследнее равенство системы (10), получим дисперсионное уравнение для поверхностных волн, кубическое относительно γ
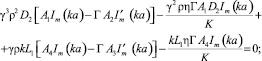(11)
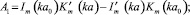
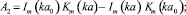
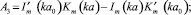
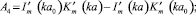
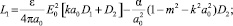
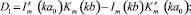
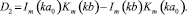
Уравнение (11) – кубическое и может быть приведено к так называемому неполному кубическому уравнению [2] с дискриминантом
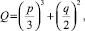
где p и q выражаются через коэффициенты уравнения (11). При выполнении условия Q > 0 существует волновое движение, поскольку при этом уравнение (11) имеет два комплексно сопряженных корня. При Q ≤ 0 волновых движений нет, так как все три корня уравнения (11) действительные.
Конкретные числовые расчеты с дисперсионным уравнением (11) проводились для следующих значений параметров: ρ = 1 г/см3, α = 73 г/с2, η = 0,01 г/см∙с, Γ = 0,8, K = 0,02 см2, 0 < k < 2 см–1, ε = 1, 0 ≤ E0 ≤ 40 ед. СГС (1 ед. СГС = 300 вольт/см).
Случай симметричных возмущений (m = 0) был рассмотрен в [6].
Остановимся подробнее на исследовании влияния напряженности электрического поля E и волнового числа k на коэффициент затухания β и частоту колебаний волны для несимметричных возмущений (m = 1, m = 2). Случай m > 2 не рассматривается, поскольку при этом нарушается физическое ограничение (k2K)/(Γ ⟨⟨ 1).
Для значений a = 0,1 см, a0 = 1,1 см, b = 2 см, 0 < k < 2 см–1, ε = 1, 0 ≤ E0 ≤ 40 ед. СГС, интервал 0 < k < 2 см–1 делится критической точкой kc (λc = 2π/kc), которая находится из условия Q = 0, на два интервала. В интервале 0 < k < kc волны отсутствуют: происходит нарастание возмущений (β < 0). Амплитуда растет с наибольшей скоростью при k = km. Размер образующихся при распаде жидкого столба капель равен λm ≈ 2π/km [1].
В таблице приведены значения kc для случаев m = 1 и m = 2 в зависимости от значений напряженности электрического поля.
Значения kc, см–1, найденные для a = 0,1 см, a0 = 1,1 см,b = 2 см
|
E0, ед. СГС |
0 |
10 |
20 |
30 |
40 |
|
m = 1 |
0,909 |
0,970 |
1,152 |
1,466 |
1,957 |
|
m = 2 |
0,909 |
0,996 |
1,240 |
1,632 |
2,190 |
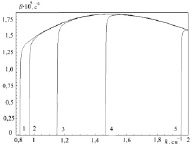
Рис. 1. Зависимость коэффициента затухания β от волнового числа k; параметр m = 1, a = 0,1 см, a0 = 1,1 см, b = 2 см. Номерами 1–5 обозначены кривые, рассчитанные соответственно для E0 = 0, 10, 20, 30, 40 ед. СГС
Из рис. 1 видно, что с ростом волнового числа k значения коэффициента затухания волны сначала резко возрастают, а затем, по достижении максимума, монотонно убывают.
С ростом значения напряженности электрического поля графики сдвигаются вправо вдоль оси x. При этом βmax достигается при k ≈ 1,45 c–1.
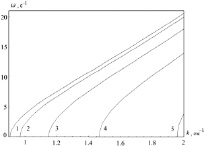
Рис. 2. Зависимость частоты от волнового числа k при m = 1 и фиксированных значениях a = 0,1 см, a0 = 1,1 см, b = 2 см. Номерами 1–5 обозначены кривые, рассчитанные для E0 = 0; 10; 20; 30; 40 ед. СГС соответственно
Из рис. 2 видно, что с ростом волнового числа значения частоты колебаний увеличиваются. При каждом заданном k частота уменьшается с ростом E.
На рис. 3 представлена зависимость коэффициента затухания β от волнового числа k; параметр m = 2, a = 0,1 см, a0 = 1,1 см, b = 2 см. Номерами 1–4 обозначены кривые, рассчитанные соответственно для E0 = 0, 10, 20, 30 ед. СГС.
Из рис. 3 видно, что с ростом волнового числа k значения коэффициента затухания возрастают. С ростом значения напряженности электрического поля графики сдвигаются вправо вдоль оси k. Следует отметить, что после резкого возрастания ветви графиков сливаются в одну линию независимо от напряженности электрического поля (см. рис. 3).
При m = 2 графики зависимости от k аналогичны приведенным на рис. 2.
При m = 1 с ростом невозмущенной поверхности жидкости a0 значения коэффициента затухания и частоты колебаний уменьшаются при каждом заданном значении волнового числа k и зафиксированных значениях прочих параметров. С ростом радиуса пористого цилиндра значения коэффициента затухания волны увеличиваются, а частоты колебаний – уменьшаются при каждом заданном значении волнового числа k и зафиксированных значениях прочих параметров.
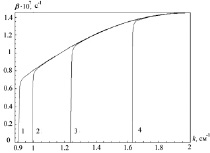
Рис. 3
При m = 1 затухание возмущений сильнее, а частота ω(k) волны меньше, чем при m = 2 при каждом заданном k и одинаковых значениях прочих параметров. В области существования волн частота ω увеличивается, а коэффициент затухания β уменьшается с увеличением радиуса a0 жидкого столба при каждом заданном значении волнового числа k и зафиксированных значениях прочих параметров.
Автор благодарит профессора Н.Г. Тактарова за постановку задачи и ее обсуждение.
Исследование выполнено при поддержке Министерства образования и науки Российской Федерации, соглашение 14.132.21.1353.
Рецензенты:
Тактаров Н.Г., д.ф.-м.н., профессор, ФГБОУ ВПО «Мордовский государственный педагогический институт имени М.Е. Евсевьева», г. Саранск;
Малыханов Ю.Б., д.ф.-м.н., профессор, ФГБОУ ВПО «Мордовский государственный педагогический институт имени М.Е. Евсевьева», г. Саранск.
Работа поступила в редакцию 09.10.2013.