В колосниковых цементных холодильниках через слой клинкерных гранул, обожженных в печи, продувается поток воздуха, который охлаждает клинкер, рекуперируя его теплоту для возврата в печь. Эффективность работы холодильника влияет на расход топлива для обжига и коэффициент полезного действия печного агрегата [2–4, 6, 9]. Целью работы являлся анализ влияния режимных параметров на эффективность работы клинкерного колосникового холодильника с переталкивающей решеткой методами компьютерного моделирования.
Описание модели
Для моделирования процесса охлаждения материала в колосниковом клинкерном холодильнике с переталкивающей решеткой [7, 8, 10, 11] с использованием сиcтемы Ansys Fluent была построена упрощенная двумерная компьютерная модель горячей секции колосникового клинкерного холодильника [5].
Расчетная сетка представляет собой поли- или монодисперсный слой гранул, перемещающийся с постоянной скоростью по горизонтальному направлению, над которым расположена воздушная камера (рис. 1).
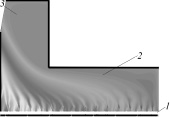
Рис. 1. Распределение температурного поля в камере горячей секции при установившемся режиме: 1 – слой клинкера; 2 – воздушная камера; 3 – шахта, соединяющая холодильник и печь
Воздух с температурой 300 К поступает под колосники, проходит через слой клинкерных гранул в воздушную камеру и через шахту подается в печь. Модель двумерная, каждая гранула представляет собой отдельную область, разбитую расчетной сеткой на контрольные объемы, что позволяет представить гранулу как отдельный объект со своим температурным полем, изменение которого в общем случае нелинейно и позволяет учесть влияние тепловой инерции гранул на общий теплообмен. Расход воздуха, проходящего через слой клинкерных гранул, задавался в виде граничных условий – массового расхода в нижнем сечении модели (под слоем). Моделирование охлаждения слоя несколькими дутьевыми машинами осуществляется установлением отдельных граничных условий на каждом участке секции. Теплофизические свойства материала и коэффициенты теплообмена в слое были приняты согласно данным работы [1]. Расчет проводился до стабилизации расчетных полей. На рис. 2 представлены участки слоя для некоторых вариантов, использованных в расчетах для различной высоты слоя и диаметра гранул.
а  б
б 
Рис. 2. Модель охлаждения монодисперсого (а) и полидисперсного (б) слоя
Упрощение модели заключается в отсутствии перемешивания слоя гранул, производимого в холодильнике колосниковыми решетками, и задании непрерывного движения слоя, тогда как в отличие от этого в колосниковом холодильнике происходит циклическое движение групп колосников. Реализация перемешивания в рамках данной модели возможна, однако требует её усложнения – включения в модель подвижных колосников, использование динамической перестраиваемой сетки между перемещающимися гранулами и колосниками, подключения уравнений взаимодействия гранул между собой и элементами холодильника (подвижными колосниками и неподвижной решеткой), что усложнит расчет и снизит его точность. Такая задача, тем не менее, может быть решена даже в трехмерной постановке благодаря возможности распараллеливания вычислений в Ansys Fluent на кластере или распределенной сети из нескольких компьютеров.
Следует отметить, что по мере переталкивания слоя подвижными колосниками мелкие гранулы просыпаются вниз, что также может влиять на аэродинамику слоя и на теплообмен. Также в модели не учтено пыление, возникающее вследствие разрушения гранул.
Адекватность разработанной модели подтверждает соответствие результатов моделирования параметрам работы промышленных колосниковых холодильников [3, 6].
Результаты моделирования
Для исследования были смоделированы случаи, представленные в таблице.
В численных экспериментах величина массового расхода воздуха принималась равной 2 кг/кг клинкера, скорость колосников определяла высоту слоя. Расход материала является фиксированным значением, высота слоя является вычисляемым параметром, определяемым через расход материала и скорость движения слоя.
На рис. 3 представлены полученные значения средних температур материала по длине секции, воздуха на выходе из слоя, перепад давления в слое при установившемся режиме и расходе воздуха 2 кг/кг клинкера. На рис. 4 показаны температура воздуха на выходе из слоя, средняя температура материала и массовый расход по длине секции для характерных случаев.
Варианты для моделирования
|
№ п/п |
Диаметр гранул, мм |
Тип засыпки |
Высота слоя, м |
Температура клинкера на входе в холодильник, K |
Средняя температура воздуха на выходе из слоя в начале секции, К |
Средняя температура материала на выходе из холодильника, K |
Средняя температура воздуха в конце секции, К |
|
1 |
13 |
Монодисперсная |
0,1 |
1470 |
908 |
667 |
464 |
|
2 |
13 |
0,15 |
1470 |
1248 |
682 |
523 |
|
|
3 |
17 |
0,1 |
1470 |
1086 |
739 |
566 |
|
|
4 |
17 |
0,15 |
1470 |
1200 |
760 |
607 |
|
|
5 |
13, 17 |
Слой из гранул двух диаметров |
0,15 |
1470 |
1230 |
690 |
530 |
|
6 |
10…25 |
Полидисперсная (диаметры гранул с нормальным распределением фракций, крупные гранулы расположены вверху) |
0,15 |
1470 |
1187 |
653 |
460 |
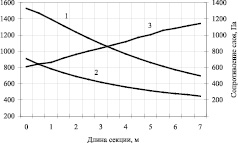
Рис. 3. Параметры слоя по длине секции: 1 – средняя температура материала; 2 – средняя температура воздуха на выходе из слоя; 3 – сопротивление слоя
а 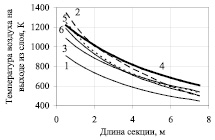 б
б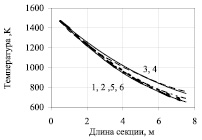
Рис. 4. Температура воздуха (а) и клинкера (б) по длине секции, обозначения кривых соответствуют нумерации в таблице
Анализ результатов
В результате моделирования можно сделать выводы, что сопротивление слоя обратно пропорционально температуре материала и диаметру гранул (доле мелкой фракции) и прямо пропорционально высоте слоя. Полидисперсный слой материала характеризуется сопротивлением, лежащим между сопротивлением монодисперсных слоев из самых крупных и самых мелких гранул. Следовательно, упрощенная модель с принятыми допущениями адекватна и результаты моделирования для моно- и полидисперсного слоя клинкера можно использовать для оценки эффективности и оптимизации режимов работы клинкерного холодильника.
В результате моделирования получены зависимости, характеризующие различные режимы охлаждения слоя клинкера (рис. 5).
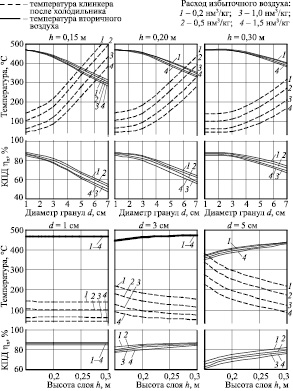
Рис. 5. Характеристики работы колосникового холодильника при различном диаметре клинкерных гранул d и высоте слоя h (расход вторичного воздуха во всех случаях 1,8 нм3/кг∙кл; высота слоя одинакова во всех секциях)
Объем воздуха, подаваемого в холодильник, равен сумме объемов вторичного и избыточного воздуха. Из рис. 5 видно, что при увеличении этого объема температура клинкера после холодильника значительно снижается, но при этом из-за роста потерь теплоты с избыточным воздухом происходит снижение КПД.
С увеличением диаметра гранул клинкера процесс теплопередачи в слое ухудшается и эффективность охлаждения падает. Но при этом необходимо отметить, что при диаметре гранул до 2…3 см показатели работы холодильника меняются мало, таким образом этот диапазон является интервалом его устойчивой работы.
Выводы
Разработанная компьютерная модель позволяет исследовать режим работы колосникового холодильника при разном фракционном составе охлаждаемого материала. Установлено, что при диаметре гранул до 2…3 см показатели работы колосникового холодильника меняются мало, таким образом, этот диапазон является интервалом устойчивой работы.
Рецензенты:
Беседин П.В., д.т.н., профессор кафедры технологии стекла и керамики, ФГБОУ ВПО «Белгородский государственный технологический университет им. В.Г. Шухова», г. Белгород;
Носов О.А., д.т.н., профессор, проректор по научной работе, НОУ ВПО «Белгородский инженерно-экономический институт», г. Белгород.
Работа поступила в редакцию 09.10.2013.



