Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Основной задачей любого руководителя является принятие решений, и применение адекватных методов принятия решений играет большую роль в повышении эффективности его работы. Существуют разные определения понятия «решение», но во всех случаях это – выбор альтернативы.

В современных условиях развития российской экономики особое значение приобретает принятие решения о правильном выборе инновационного проекта из альтернативных вариантов, что сводится к сравнительному анализу их эффективности. Распространенным способом поиска решения является коллективное обсуждение, однако этот процесс требует много времени и может оказаться субъективным, поскольку проводится в условиях значительной неопределенности исходной информации [8].

Альтернативой является привлечение к сравнительному анализу эффективности проектов экспертов, и здесь крайне важна рациональная организация их работы. Один из эффективных способов сравнительного анализа проектов – это опрос группы экспертов по заранее разработанной и уточненной с их привлечением модели с помощью системы подготовки принятия решения (СППР). В частности, такой СППР является экспертно-аналитическая система Expert Decide, разработанная в 2000–2001 гг. специалистами Орловского государственного технического университета (ОГТУ) и Орловской региональной академии государственной службы (ОРАГС) [2]. Эта система поддерживает алгоритмы метода аналитических иерархий (МАИ, в англо-американской литературе AHP – analitical hierarchy process [6]), который является одним из доведенных до практического применения методов системного анализа и завоевал сторонников во всем мире. Система обладает дружественным интерфейсом и рассчитана на работу с группой экспертов.

Известны и другие системы подготовки принятия решения, использующие алгоритмы МАИ/AHP, в частности, система «MPRIORITY 1.0» [1]. Интересной особенностью этой СППР является использование шаблонов – готовых иерархий для «стандартных» задач принятия решений. Используя поставляемые вместе с программой стандартные шаблоны, пользователь может выбрать наиболее подходящий для текущей задачи принятия решений, загрузить его, подкорректировать в случае необходимости и приступить к решению своей задачи принятия решений. При этом пользователь, работая в той или иной области (например, в медицине, в банковском деле и т.д.), накапливая опыт решения различных задач принятия решений, может создать свою библиотеку шаблонов, которую потом можно будет использовать другим пользователям, работающим в аналогичных областях.

Алгоритмы МАИ/AHP были также положены в основу более поздней разработки – экспертно-аналитической системы Expert Solution 1.0 [5], специально предназначенной для сравнительного анализа альтернативных инновационных проектов в условиях риска и информационной неопределенности. Эта разработка Российского экономического университета им. Г.В. Плеханова выгодно отличается от аналогов модульным построением, в основе которого лежит реализация алгоритмов моделей прямой и обратной иерархии, что позволяет проводить совершенствование системы без существенных изменений внутри модулей. Кроме того, система Expert Solution 1.0 поддерживает алгоритмы расширения метода анализа иерархий – метода аналитических сетей [7]. Все это, вместе взятое, повышает надежность принятия решения в условиях информационной неопределенности.

Таким образом, можно говорить о широком признании метода анализа иерархий не только за рубежом, но и в нашей стране. Приведем высказывание генерального директора консалтинговой группы МБИ В.Г. Литвинова: «Внушительная история успешного применения указанного метода в частных и государственных организациях разных стран показала его высокую практическую эффективность. Метод анализа иерархий обеспечивает интеграцию многих факторов, вовлеченных в решения, упрощает поиск решений путем представления сложной проблемы в виде последовательного анализа более простых задач» [6].

В то же время существует ряд проблем обоснованности применения МАИ/AHP, которые стали причиной критики некоторых специалистов. Так, в работе [4] проводится обоснование тезиса, что метод анализа иерархий, предполагающий для проведения анализа многокритериальных задач принятия решений с использованием аддитивной функции ценности оценивание предпочтений в шкале отношений, несостоятелен. Действительно, из теории многокритериальных оценок известно, что аддитивная свертка частных критериев в обобщенный критерий используется в случае их коррелированности, тогда как в случае отсутствия сильных корреляций частных критериев, что является одним из требований в методе анализа иерархий, более подходящей является их мультипликативная свертка.

В связи с этим несоответствием нами выполнен имитационный эксперимент, цель которого – сравнить два альтернативных вида свертки – аддитивную и мультипликативную; очевидно, что наиболее вероятное значение глобального вектора приоритетов альтернатив будет определяться как среднее арифметическое этих двух оценок. В основу этого эксперимента положена иерархическая модель риск-анализа трех альтернативных проектов в сфере автомобилестроения с условными названиями «Ford Focus II», «KIA Rio 2» и «Тойота Камри» по уровню каждого из пяти факторов риска – финансового, риска сбыта, политического, производственного и рыночного риска [9].

В экспертно-аналитической системе Expert Solution 1.0 задача риск-анализа альтернативных проектов по пяти факторам риска сводится к генерации концептуальной иерархической модели, на верхнем уровне которой цель – фокус «оценка риска проектов», на среднем – факторы риска (финансовый риск, риск сбыта, политический, производственный и рыночный риски), на нижнем – сравниваемые проекты. Затем эксперту предъявляется матрица парных сравнений – вначале критериев (факторов риска), затем пять матриц парных сравнений альтернатив (по каждому из факторов риска). Матрицы заполнены единицами, что отвечает их равной значимости, и эксперт на выплывающей шкале сравнений выбирает суждение о фактическом соотношении значимости критериев и альтернатив.

Результатом опроса является информационная модель риск-анализа по каждому из экспертов, одна из которых представлена на рис. 1.

Отметим, что синтез локальных векторов весов рисков альтернативных проектов в глобальный вектор в системе Expert Solution 1.0 проводится по формуле принятой в МАИ/AHP аддитивной свертки. Можно, однако, применить и иной вид свертки, например, мультипликативную, воспользовавшись данными по локальным векторам весов риска проектов и вектору приоритетов факторов риска. Вообще говоря, глобальные векторы рисков альтернативных проектов, вычисленные по формуле аддитивной и мультипликативной свертки, будут различаться. Предположительно, эти различия будут тем меньше, чем выше степень согласованности основной матрицы – матрицы сравнений факторов риска.

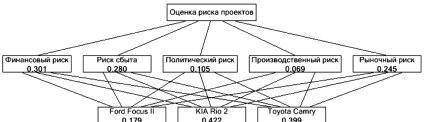
Рис. 1. Информационная модель риск-анализа альтернативных проектов (получена в системе Expert Solution 1.0)

Для проверки этого предположения нами по исходным данным для локальных векторов весов риска проектов и вектору приоритетов факторов, приведенным в табл. 1, в редакторе данных пакета SPSS Base [10] рассчитаны компоненты глобального вектор уровня риска альтернативных проектов по формулам аддитивной и мультипликативной свертки. Полученные результаты, приведенные в двух последних строках таблицы, показывают, что эти векторы различаются, но не на много, и ранжирование альтернативных проектов по уровню риска остается тем же.

Таблица 1

Расчет глобальных векторов уровня риска проектов

Оценим разницу между глобальными векторами риска проектов, вычисленными по формулам аддитивной и мультипликативной свертки, количественно. Автор метода анализа иерархий Т. Саати в работе [6] приводит две меры отклонения между векторами: среднеквадратичное отклонение (СКО) и медианное абсолютное отклонение (МКО), при этом отмечает, что для того, чтобы показать, насколько они малы в абсолютных значениях, их надо разделить на среднее значение приоритета, т.е. на 1/n, где n – число компонент вектора. Размерность глобальных векторов риска проектов n = 3, отсюда значение меры отклонения (МО) составит:

МО = {1/n Σ(w1i – w2i)2}1/2/(1/n) = {1/3 [(0,179 – 0,187)2 + (0,422 – 0,429)2 + + (0,399 – 0,384)2]}1/2 / (1/3) = 0,022.

Это значение меры отклонения меньше 0,1, и, по Т. Саати, можно считать, что оба вектора почти одинаковы.

Для оценки степени согласованности иерархий применим процедуру, предложенную в работе [6]. Согласно теории метода анализа иерархий, степень согласованности информационной иерархической модели определяется величиной отношения согласованности OC

OC = Icoord/Ierr, (1)

где индекс согласованности Icoord рассчитывается по формуле

Icoord = (lmax - n)/(n - 1). (2)

Здесь lmax – максимальное собственное число матрицы парного сравнения; n — порядок матрицы, а Ierr — случайный индекс, т.е. индекс согласованности сгенерированной случайным образом по шкале от 1 до 9 обратносимметрической матрицы с соответствующими обратными величинами элементов (значения Ierr приведены в [6]). Согласованность матрицы тем выше, чем меньше lmax отличается от ее размерности n.

Понятие согласованности в работе [6] обобщено на всю иерархию следующим образом: индекс согласованности, полученный из матрицы парных сравнений, умножается на приоритет критерия, относительно которого проведено сравнение, и к этому числу добавляются аналогичные результаты для всей иерархии. Затем эта величина сравнивается с соответствующим индексом, полученным как сумма случайно сформированных индексов, взвешенных соответствующими приоритетами. В рассматриваемом случае имеем:

– вектор приоритетов факторов риска (критериев)

Wкритер = (0,301; 0,280; 0,105; 0,069; 0,245);

– индекс согласованности матрицы парного сравнения

ИС = (5,07 – 5)/(5 – 1) = 0,018;

– вектор индекса согласованности матриц сравнения проектов (альтернатив)

ИСальтер = (0,026; 0,004; 0,026; 0,000, 0,009).

Отсюда индекс согласованности иерархии

ИСИ = 0,016 + (0,301;0,280;0,105;0,069;0,245)× ×(0,026;0,004;0,026;0,000;0,009)т = 0,016 + 0,014 = 0,030.

Случайный индекс иерархии в целом определяется соотношением

ИИС = 1,12 + (0,301;0,280;0,105;0,069;0,245)× ×(0,58;0,58;0,58;0,58;0,58)т = 1,12 + 0,58 = 1,7.

Здесь 1,12 и 0,58 – случайные индексы матрицы пятого и третьего порядка соответственно [6, с. 34].

Из сравнения индекса согласованности иерархии ИСИ с величиной случайного индекса следует, что отношение согласованности рассматриваемой иерархии составляет величину ОСИ = ИСИ/ИИС = 0,030/1,7 = 0,018. Это меньше критического значения ОСИ = 0,1 и свидетельствует о хорошей согласованности парных сравнений в рассматриваемой информационной модели риск-анализа альтернативных проектов.

Полученные результаты позволяют перейти к выявлению связи меры отличия глобальных векторов рисков альтернативных проектов МО, вычисленной по формуле аддитивной и мультипликативной свертки, со степенью согласованности основной матрицы – матрицы парных сравнений факторов риска. Для решения этой задачи нами выполнен имитационный эксперимент, суть которого – в изменении элементов матрицы парных сравнений факторов риска в небольших пределах, на ±(1–2) делений девятибальной шкалы отношений Т. Саати. Остальные пять матриц – матрицы парных сравнений альтернативных проектов по каждому фактору риска – при этом сохраняем неизменными, так что в расчете значений ИСИ – индекса согласованности иерархии – заметно изменяться будет только первое слагаемое, второе же останется практически таким же. Что касается случайного индекса иерархии ИИС, то для всех вариантов имитации его значения составят 1,7.

Результаты имитационного эксперименты приведены в табл. 2, а на диаграммах рис. 2 зависимость различия векторов весов рисков проектов, рассчитанных по формулам аддитивной и мультипликативной свертки, от степени согласованности суждений в модели риск-анализа представлена в наглядном графическом виде.

Из графиков на рис. 2 видно, что между мерой различия векторов весов риска проектов, рассчитанных по формулам аддитивной и мультипликативной свертки, и показателями согласованности – отношением согласованности матрицы парных сравнений факторов риска, с одной стороны, и отношением согласованности иерархии модели риск-анализа в целом, с другой, наблюдаются тесные линейные зависимости.

Таблица 2

Результаты имитационного эксперимента по зависимости различия векторов весов рисков проектов, рассчитанных по формулам аддитивной и мультипликативной свертки, от степени согласованности суждений в модели риск-анализа

а)

б)

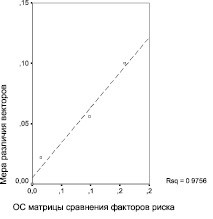
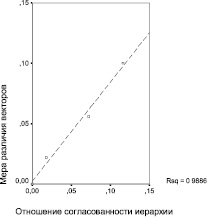
Рис. 2. Зависимость меры различия векторов весов риска проектов, рассчитанных по формулам аддитивной и мультипликативной свертки: а – от отношения согласованности матрицы парных сравнений факторов риска; б – от отношения согласованности иерархии модели риск-анализа в целом

Эти зависимости формально можно выразить следующими уравнениями:

МРВ = 0,00509 + 0,582∙ОС; (3)

МРВ = 0,00221 + 0,821∙ОСИ, (4)

где МРВ – мера различия векторов весов риска проектов, рассчитанных по формулам аддитивной и мультипликативной свертки; ОС – отношение согласованности матрицы парных сравнений факторов риска; ОСИ – отношение согласованности иерархии модели риск-анализа в целом. При этом коэффициенты 0,582 и 0,821 в выражениях (3) и (4) отражают прирост меры различия векторов весов риска проектов, рассчитанных по формулам аддитивной и мультипликативной свертки, при увеличении предикторов на единицу.

На основании этих моделей можно оценить показатели эластичности МРВ по параметрам согласованности ОС и ОСИ. Учитывая, что средние значения зависимой переменной и предикторов в выражениях (3) и (4) составляет МРВср = 0,0445, ОСср = 0,06775 и ОСИср = 0,0515, получим:

ЭМРВ/ОС = 0,582∙0,06775/0,0445 = 0,866;

ЭМРВ/ОСИ = 0,812∙0,0515/0,0445 = 0,940.

Полученные оценки эластичности интерпретируются следующим образом: при увеличении отношения согласованности матрицы парных сравнений факторов риска и отношения согласованности иерархии модели риск-анализа в целом на 1 % мера различия векторов весов риска проектов, рассчитанных по формулам аддитивной и мультипликативной свертки, увеличивается на 0,866 и 0,940 % соответственно. Это свидетельствует о высокой степени влияния согласованности суждений экспертов на результат экспертизы.

По представленным в данной статье результатам можно сделать выводы:

1) с ростом согласованности матриц парных сравнений различие глобальных векторов приоритетов альтернатив, рассчитанных по формулам аддитивной и мультипликативной свертки, уменьшается, и при достаточно высокой согласованности суждений по матрицам парных сравнений – не хуже ОС = 0,10 – находится в допустимых пределах – не хуже 0,10;

2) выбор формы свертки локальных векторов приоритетов альтернатив в глобальный вектор практически не влияет на результаты ранжирования сравниваемых проектов.

Тихомирова Е.И., д.э.н., профессор, декан факультета математической экономики и информатики, ФГБОУ ВПО «Российский экономический университет имени Г.В. Плеханова», г. Москва;

Хохлова О.А., д.э.н., профессор, заведующий кафедрой статистики, ФГБОУ ВПО «Российский экономический университет имени Г.В. Плеханова», г. Москва.

Работа поступила в редакцию 17.10.2013.