В последнее время активно ведется обсуждение различных способов организации детонационного горения в перспективных воздушно-реактивных и ракетных двигателях. Чтобы правильно понять суть этих проектов, важно ясно представлять, что такое стационарный и нестационарный газодинамический разрыв (ГДР), ударная волна, и чем они отличаются от волны детонационной, которая также является газодинамическим разрывом. Условимся для определенности считать, что детонационная волна – это ударная волна, возникшая вследствие химической реакции окисления. А просто ударная волна – это газодинамический разрыв, который образуется взаимодействием сверхзвукового потока с твердой стенкой, острой кромкой или в результате пересечения (интерференции) других ГДР.
Развитие теории интерференции газодинамических разрывов
В настоящее время (в последние 19 лет) создана теория и математический аппарат, достаточный для проектирования оптимальных ударно-волновых структур (УВС) в детонационной камере сгорания, работающей как в стационарном, так и в импульсном режимах. Научная группа под руководством В.Н. Ускова последовательно развила теорию экстремальных УВС. Сначала теория интерференции стационарных газодинамических разрывов была обобщена В.Н. Усковым и С.Л. Старых на случай разрывов второго порядка [4–6]. Ими была исследована зависимость неравномерностей течения за разрывом от кривизны разрыва и неравномерностей течения перед ним. Затем теория была дополнена в работах В.Н. Ускова, А.В. Омельченко и М.В. Чернышева теорией интерференции одномерных бегущих волн и взаимодействия косых нестационарных волн [7, 9, 11]. Параллельно аспирантом В.Н. Ускова Тао Ганом была разработана теория оптимальных тройных конфигураций ударных волн сначала в равномерном потоке, а затем и в неравномерном [8]. И наконец, в работах В.Н. Ускова, М.В. Чернышева и П.С. Мостовых [10, 12] она была обобщена на случай тройных конфигураций ударных волн в нестационарном и неравномерном потоке газа. Автором настоящей работы была развита теория низкочастотных колебаний ударных волн на примере течения в канале с внезапным расширением [1–3].
Геометрический смысл уравнений газовой динамики сверхзвуковых течений
В основе каждого раздела физики лежит своя геометрия пространства параметров. Геометрия Минковского описывает пространство Специальной Теории Относительности, Риманова геометрия – Общей Теории Относительности, Симплектическая геометрия – классической механики и т.п. Для того, чтобы иметь возможность воспользоваться достижениями математиков в части классификации и структурной устойчивости ударно-волновых структур (УВС), необходимо дать определения газодинамическим понятиям в терминах симплектической геометрии. По современным представлениям газодинамические переменные образуют многомерное гиперпространство, а уравнения Эйлера, описывающие течения идеального газа, задают в нем гиперповерхность, кривизна которой определяется газодинамическими неравномерностями Ni (неизобаричность, кривизна линии тока и завихренность):
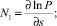
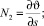
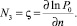
В осесимметричном случае уравнения Эйлера, записанные с помощью неравномерностей, выглядят в естественной системе координат, связанной с линиями тока, следующим образом:
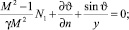
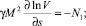
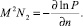
В уравнениях – n – длина нормали к линиям тока; s – длина дуги вдоль линии тока; P – давление; ϑ – угол наклона вектора скорости; P0 – полное давление; ζ – завихренность. Первое выражение – уравнение неразрывности. Второе и третье – проекции уравнения движения на оси естественной системы координат, связанной с линиями тока. Как известно, сверхзвуковые течения могут содержать области, где параметры меняются резко, скачком. В рамках модели идеального газа в таких случаях говорят о существовании газодинамических разрывов (ГДР).
Обобщение понятия поверхности – многообразие. Многообразие представляет собой произвольное множество точек, представленное в виде объединения конечного числа областей евклидового пространства, в каждой из которых заданы локальные координаты.
Ударная и детонационная волна как особенность отображения проектирования многообразия газодинамических параметров
Рассмотрим для простоты одномерное уравнение движения идеального газа (уравнение Эйлера):
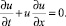
Это уравнение описывает поле скоростей свободно движущихся по прямой частиц. Закон свободного движения частицы имеет вид:
x = ϕ(t) = x0 + vt,
где v – скорость частицы. Функция ϕ удовлетворяет уравнению Ньютона. По определению: dϕ/dt = u(t, ϕ). Продифференцировав последнее соотношение по t, получаем уравнение:
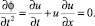
Таким образом, описание движения при помощи уравнения Эйлера для поля и при помощи уравнения Ньютона для частиц эквивалентны. Известно, что квазилинейные дифференциальные уравнения в частных производных решаются с помощью построения характеристик. Каждому многообразию соответствует свое характеристическое поле. Характеристики – фазовые кривые характеристического поля. Уравнение характеристик уравнения Эйлера эквивалентно уравнению Ньютона. Таким образом, задачу о распространении волны можно решить путем построения характеристик, вдоль которых движутся материальные частицы. На рис. 1, 2 показано, как решается уравнение Эйлера с помощью характеристик.
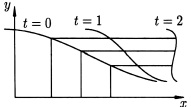
Рис. 1. Решение уравнения Эйлера с помощью характеристик
На плоскости y–x задана начальная функция y = u0(x)t = 0. Уравнения характеристик t’ = 1, y’ = 0, x’ = y. В моменты времени t = 1, t = 2 и т.д. решение строится путем переноса вдоль характеристик значений в начальный момент времени. Интегральная поверхность неоднозначно проектируется на плоскость x–t (рис. 2). Отображение y(x) перестает быть графиком функции, т.е. имеются значения х, которым соответствует несколько значений y. Кривая критических значений проектирования (касательная к поверхности вертикальна) имеет точку возврата (рис. 3).

Рис. 2. Интегральная поверхность перестает быть графиком функции y(x)
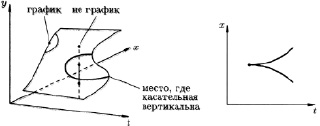
а б
Рис. 3. ГДР – особенность отображения проектирования многообразия параметров
Нарушение единственности решения можно трактовать как свободное прохождение потоков частиц друг сквозь друга. С другой стороны, при большой плотности частиц их взаимодействием нельзя пренебречь. В этом случае, уравнение Эйлера заменяют уравнением Бюргерса, которое учитывает взаимодействие частиц газа внутри ударной волны:
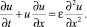
При малых ε оно приближает уравнение Эйлера в областях плавного изменения параметров. Справа и слева от ударной волны течение описывается уравнениями Эйлера, внутри ударной волны (газодинамического разрыва) – уравнением, подобным уравнению теплопроводности.
Таким образом, ударная волна или газодинамический разрыв (ГДР) – это особенность отображения проектирования многообразия газодинамических параметров (рис. 3), их взаимодействие образует ударно-волновые структуры (УВС).
В рассматриваемом одномерном случае ударная волна может быть сформирована движущимся по трубе поршнем. Если скорость поршня выше некоторой критической величины, то распространяющиеся от его поверхности волны сжатия догоняют друг друга, и единственность решений нарушается. Возникает разрыв значений. До волны давление и другие параметры остаются такими же, как в невозмущенной среде, а сразу за разрывом давление скачком увеличивается. Ударная волна может возникнуть и в результате химической реакции горения, в этом случае ее называют детонационной. Предположим, что в предварительно подготовленной топливной смеси каким-то образом (искрой, теплопередачей, сжатием) создали условия для возбуждения реакции окисления (горения). Топливная смесь в определенных условиях может сдетонировать.
При детонации (быстром горении) воспламенение, реагирующее смеси, происходит в результате сжатия в лидирующей Ударной Волне (УВ), которая предшествует зоне химических реакций. Ударная волна распространяется со сверхзвуковой скоростью. Простейшей моделью детонационного горения является модель Зельдовича – Неймана (рис. 4).
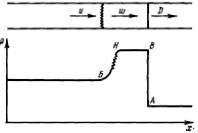
Рис. 4. Модель детонации Зельдовича – Неймана: D – детонационная волна; ω – зона индукции; u – продукты сгорания; А-В – газодинамический разрыв; Н-В – зона образования свободных радикалов; Н-Б – волна разрежения, в которой происходят химические реакции окисления
Заключение
Представление о сверхзвуковых течениях в терминах симплектической геометрии дает в руки исследователя важный инструмент, обладающий общностью анализа, как скачков уплотнения, так и ударных и детонационных волн. Это позволяет конструировать сложные конфигурации ударных и детонационных волн в соответствии с некоторым выбранным критерием оптимальности.
Рецензенты:Пеленко В.В., д.т.н., профессор, заместитель директора по учебной работе Института Холода и Биотехнологий, ФГБОУ «Санкт-Петербургский национальный исследовательский университет информационных технологий, механики и оптики», г. Санкт-Петербург;
Цветков О.Б., д.т.н., профессор, заведующий кафедрой «Теоретические основы тепло- и хладотехники» Института Холода и Биотехнологий, ФГБОУ «Санкт-Петербургский национальный исследовательский университет информационных технологий, механики и оптики», г. Санкт-Петербург.
Работа поступила в редакцию 17.10.2013.



