Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

В настоящее время для решения большого количества практических задач в различных предметных областях человеческой деятельности широкое применение получили экспертные системы. Их появление обусловлено необходимостью тиражирования знаний экспертов в связи с возрастанием числа сложных объектов и систем, при работе с которыми знаний и квалификации обычных специалистов становится недостаточно.

Для описания сложного объекта, как правило, приходится оперировать данными, обладающими следующими особенностями: большой объем, разнотипность, наличие нечеткости в данных, отсутствие части исходных данных, большое количество параметров. Достоинством экспертных систем является возможность их эффективного применения при решении практических задач в указанных условиях. Среди всех классов экспертных систем особое место занимают диагностические системы ввиду важности решения данной задачи в широком диапазоне областей: экономическая, медицинская, техническая диагностика и др.

При построении экспертной системы перед ее разработчиками встают проблемы добычи и формализации знаний. Существует два основных способа получения знаний [2]: ручной и автоматизированный. В первом случае правила формулируются экспертом, что требует от него большой аналитической работы. Во втором случае используются различные инструментальные средства формирования правил на основе алгоритмов интеллектуального анализа данных. Данный подход к получению знаний является актуальным и может быть использован при формировании баз знаний экспертных диагностических систем. Практическая реализация данной задачи требует решения вопросов выбора модели представления знаний, для диагностики состояния сложного объекта, с учетом особенностей исходных данных, а также разработки методов, моделей и алгоритмов анализа данных с целью построения модели диагностики выбранного вида.

Методика группировки параметров объекта диагностики

База знаний экспертной системы представляет собой совокупность правил, описывающих закономерности моделируемого объекта. При большом числе параметров объекта формирование базы знаний начинается с этапа группировки параметров, где каждая группа определяет закономерности «вход» – «выход» для подсистемы сложного объекта.

Рассмотрим постановку задачи разработки методики группировки параметров. Пусть дано множество параметров P = {p1, p2, ..., pk, ..., pN}, описывающих объект диагностики, множество диагнозов состояния объекта, а также множество целевых параметров 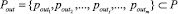, m < Nm < N, где все 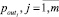принимают конечное дискретное множество значений (состояний объекта). Необходимо сформировать группы параметров 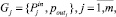где 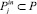 – множество входных параметров для каждого из целевого параметра 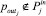, значимо влияющих на него.

Методика группировки параметров состоит из следующих основных этапов.

1. Эксперт на основе своих знаний и анализа имеющихся данных формирует множество диагнозов состояния исследуемого объекта.

2. Среди всего множества параметров {p1, p2, ..., pk, ..., pN} выбираются целевые параметры 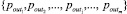, значения которых связаны с диагнозами.

3. Для каждого из целевых параметров 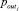эксперт, основываясь на результатах анализа корреляций между всеми параметрами pk и 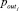, выбирает множество независимых входных параметров 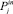, значимо влияющих на целевой.

4. Формируется множество групп параметров «вход – выход»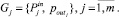

Для реализации предложенной методики необходимо наличие таблицы исходных данных. При этом каждая сформированная группа параметров описывает подсистему сложного объекта, что значительно упрощает его описание.

Модель представления знаний в экспертной системе

Для представления знаний в экспертной диагностической системе и описания зависимостей в сформированных группах параметров предлагается использовать нечетко-продукционную модель следующего вида [3]:

ЕСЛ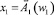И И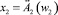

И … 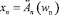ТО y = B [CF], (1)

где xi – входные переменные; wi ∈ [0, 1] – веса условий 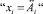; 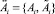, Ai – четкое значение входа;  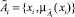– нечеткое значение входа;  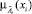– функция принадлежности; y – выходная переменная; B – четкое значение выхода, CF ∈ [0, 1] – достоверность правила.

Особенность модели представления знаний вида (1) заключается в одновременном выполнении следующих требований:

– возможность использования разнотипных входных и выходных параметров;

– возможность обработки четких и нечетких входных данных;

– учет значимости (весов) условий в правиле;

– учет значимости (достоверности) каждого правила.

В рамках нечетко-продукционных правил вида (1) возможно описание зависимостей, характеризующих состояние объектов, в различных предметных областях.

Методика построения совокупности систем правил

Следующим этапом формирования базы знаний является построение совокупности систем нечетко-продукционных правил 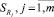, каждая из которых определяется группами параметров 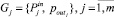, а также градациями (значениями) входных и целевого параметра группы. Разработанная методика построения совокупности систем правил состоит из трех основных шагов.

1. Для каждого параметра pk ∈ Gj определяется 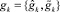, где 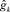 – число значений четкого параметра pk, а  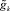– число градаций нечеткого параметра .

2. Строится множество всех комбинаций из значений входных и целевого параметров.

3. Для каждой комбинации задается правило в виде (1).

Рассмотрим пример совокупности систем нечетко-продукционных правил вида (1).

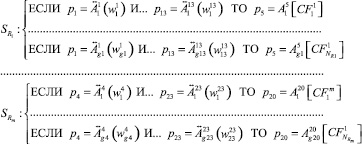
где 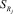 – система правил, описывающих группу параметров Gj; gk – число значений (градаций) параметра pk,  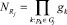– число правил в системе .

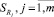Построенная совокупность систем правил вида (1) представляет параметрическую нечетко-продукционную модель состояния объекта. Параметрами модели являются функции принадлежности 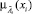в правилах, достоверность каждого правила CF, а также веса условий wi в правилах. Применение систем правил для определения состояния объекта основано на использовании специально разработанного алгоритма логического вывода.

Алгоритм логического вывода на системах правил

Для понимания организации логического вывода на системах нечетко-продукционных правил вида (1) введем следующие обозначения:

● R ∈ [0, 1] (response) – степень срабатывания условной части правила:

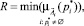
где 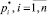 – четкие значения n входных параметров правила;  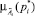– степени принадлежности входных значений 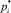к ;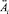

● T ∈ [0, 1] (trust) – совокупный вес условной части правила:

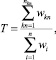
где 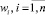 – веса всех ограничений 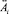на параметры в правиле,  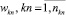– веса ограничений, значения которых известны (определены);

● C ∈ [0, 1] (complex) – комплексная оценка достоверности правила: C = R*T*CF, где CF ∈ [0, 1] (certainty factor) – достоверность правила.

Для каждой системы правил 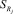, описывающей группу параметров 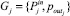, используется алгоритм логического вывода, состоящий из следующих шагов.

1. Ввод значений 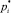входных параметров 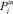группы Gj.

2. Для каждого правила Ruler системы 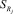расчет степени срабатывания условий Rr.

3. Формирование конфликтного множества, включающего правила с ненулевой степенью срабатывания:

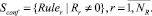
4. Для всех правил из конфликтного множества Ruler ∈ Sconf расчет совокупного веса условной части правила Tr, а также комплексной оценки Cr.

5. Разрешение конфликта – выбор правила с максимальной комплексной оценкой достоверности решения правила:

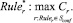
6. Получение значения 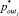выходного параметра 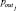выбранного правила 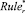в качестве искомого состояния объекта.

Предложенный алгоритм позволяет определять состояние сложного объекта.

Параметрическая адаптация модели состояния объекта

Для практического применения алгоритма логического вывода требуется, чтобы параметры нечетко-продукционной модели состояния объекта были определены. Для этого необходимо произвести ее параметрическую адаптацию к имеющимся данным [4] – определить значения параметров, при которых минимизируется ошибка – отношение числа Nfalse неправильно оцененных состояний объекта к общему объему N исходных данных:

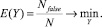(2)

Для решения данной задачи используется специально разработанная нечеткая нейронная сеть, в процессе обучения которой определяются значения параметров модели состояния объекта. На рис. 1 приведен пример структуры сети.

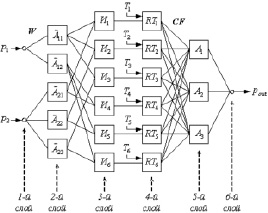
Рис. 1. Пример структуры нечеткой нейронной сети

Архитектура нечеткой нейронной сети соответствует виду нечетко-продукционных правил, а также описанному алгоритму логического вывода на них. Обучение сети основано на использовании метода градиентного спуска.

Таким образом, реализация этапов группировки параметров объекта, построения совокупности систем правил и параметрической адаптации модели к имеющимся данным позволяет сформировать базу знаний как совокупность систем нечетко-продукционных правил с идентифицированными значениями параметров.

Программный комплекс автоматизированного формирования базы знаний

Для автоматизации всех этапов интеллектуального анализа исходных данных и формирования баз знаний экспертных диагностических систем разработан программный комплекс, в основу которого положены описанные методики, модели и алгоритмы. На рис. 2 представлена структура программного комплекса.

Комплекс состоит из четырех модулей, соответствующих этапам формирования базы знаний. Для разработки программного комплекса был выбран высокоуровневый объектно-ориентированный кроссплатформенный язык программирования Java. При реализации комплекса использовалась свободная интегрированная среда разработки NetBeans IDE.

Проведение исследований на базе программного комплекса

С целью определения классифицирующей способности формируемых баз знаний произведено решение известных задач классификации из общедоступного источника UCI Machine Learning Repository [5]. В табл. 1 представлена информация о характеристиках наборов исходных данных, соответствующих решаемым задачам.

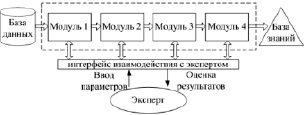
Рис. 2. Структура программного комплекса

Таблица 1

Характеристика исходных данных

В первом наборе представлены данные, соответствующие задаче диагностирования заболевания печени человека по результатам анализа его крови. Второй набор данных соответствует задаче выявления подозрительных транзакций с банковскими картами. Третий набор данных соответствует задаче принятия решения о выдаче потребительского кредита на основании анкетных данных заемщика.

В качестве меры эффективности баз знаний выступала точность классификации. Для определения значимости получаемых результатов производилось их сравнение с известными результатами других авторов [1]. В табл. 2 приведены результаты классификации.

Таблица 2

Сравнение точности методов классификации

Из таблицы видно, что классифицирующая способность сформированных нечетко-продукционных баз знаний уступает лишь классификатору на основе коллектива нейронных сетей и превосходит все известные методы классификации, участвующие в сравнении. Полученные результаты указывают на возможность эффективного использования предложенного подхода к формированию баз знаний экспертных диагностических систем.

Заключение

Описанные в работе математическое обеспечение и программный комплекс позволяют формировать базы знаний экспертных диагностических систем. Проверка работы программного комплекса на известных наборах данных показала высокую эффективность разработанного математического обеспечения и практическую пригодность программного комплекса к решению поставленных задач.

В перспективе, с целью обобщения результатов проведенного исследования и развития данного научного направления, видится решение задач, связанных с совершенствованием математического аппарата и доработкой программного комплекса до уровня аналитической платформы с широкими возможностями по формированию баз знаний промышленных экспертных систем диагностики состояния сложных объектов.

Рецензенты:

Песошин В.А., д.т.н., профессор, заведующий кафедрой компьютерных систем Казанского национального исследовательского технического университета им. А.Н. Туполева-КАИ, г. Казань;

Исмагилов И.И., д.т.н., профессор, заведующий кафедрой статистики, эконометрики и естествознания Казанского (Приволжского) федерального университета, г. Казань.

Работа поступила в редакцию 17.10.2013.