Прецизионные инерционные приборы являются важнейшими элементами систем инерциальной навигации. Данный класс приборов является перспективным и интенсивно развивающимся (постоянно проектируются и вводятся в производство новые поколения приборов с улучшенными функциональными характеристиками).
Производство современных прецизионных приборов предъявляет повышенные требования к качеству и точности их изготовления, что приводит к необходимости углубленного изучения не только конструкции приборов, но и технологии их сборки и настройки. Поэтому разработка технологических решений, направленная, во-первых, на обеспечение требуемых конструктивных параметров, во-вторых, на повышение стабильности настройки приборов, в-третьих, на сокращение трудозатрат на их изготовление, является актуальной задачей на сегодняшний день. Для решения поставленной задачи необходимо выполнение следующих условий:
– задачи должны решаться с помощью математических моделей, использующих современные программные продукты [1, 5];
– модели должны включать в себя максимально полный набор конструктивных параметров и точное описание физических процессов [4];
– при разработке модели, обеспечивающей связь конструктивных параметров с параметрами технологических процессов, должны быть учтены имеющиеся на предприятии типовые технологические процессы, имеющееся современное оборудование;
– использование системного подхода [2], когда между модулями технологического процесса устанавливается связь с использованием принципа «производитель – потребитель» и осуществляется контроль параметров процесса.
Предисследования
Некоторые прецизионные приборы:
1) датчики ускорения;
2) интегрирующие акселерометры.
Метод исследования
1) концептуальные модели;
2) причинно-следственные диаграммы;
3) расширенный спектр критичных конструктивных параметров.
Алгоритм построения и применения математических моделей, использующих расширенный спектр конструктивных параметров, представлен на рис. 1.
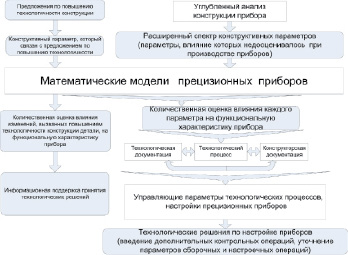
Рис. 1. Алгоритм построения и применения математических моделей, использующих расширенный спектр конструктивных параметров
В структурной схеме можно выделить две ветви. В основной ветви показано, как при углубленном анализе конструкции прибора устанавливаются конструктивные параметры, влияние которых недооценивалось при изготовлении. В результате этого формируется расширенный спектр конструктивных параметров. Разработанные математические модели позволяют учесть влияние каждого конструктивного параметра на функциональные характеристики прибора. Далее, используя данные технологической и конструкторской документации, анализируя исследуемый технологический процесс, выявляем управляющие параметры технологических процессов настройки и сборки приборов, обеспечивающие расширенный спектр конструктивных параметров. На основании полученной связи между функциональными характеристиками прибора и параметрами технологических процессов разрабатывается ряд технологических решений по настройке и сборке прибора, в частности, введение дополнительных контрольных операций, уточнение сборочных и настроечных операций.
Вторая ветвь иллюстрирует алгоритм количественной оценки влияния изменений, вызванных повышением технологичности конструкции деталей, на функциональные характеристики прибора. Вначале рассматривается предложение по повышению технологичности детали и определяется конструктивный параметр, который изменится в результате улучшения, определяются допустимые пределы данного изменения. Затем, с помощью разработанных моделей выполняется количественная оценка влияния данного изменения на функциональные характеристики прибора, позволяющая прогнозировать влияние того или иного технологического улучшения на работу прибора.
примеры использования
Приведем пример критичных конструктивных параметров для датчика ускорения (конструкция и метод расчета подробно представлены в [3]) с чувствительным элементом, совершающим вращательное движение, рис. 2, при повторных срабатываниях прибора (таблица).
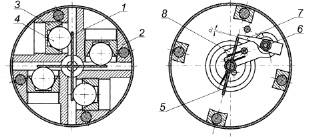
Рис. 2. Основные элементы конструкции порогового датчика: 1 – крестовина; 2 – корпус; 3 – конус; 4 – инерционное тело; 5 – фиксатор; 6 – вал; 7 – рычаг; 8 – перемыкатель
Работа механического датчика ускорения осуществляется следующим образом: при действии ускорения в любом направлении соответствующие инерционные тела (4) выкатываются из конусов (3) и поворачивают крестовину (1). Установленный на крестовине фиксатор (5) поворачивается, освобождая рычаг (7) и связанный с ним вал (6). Перемыкатель (8) замыкает требуемые контакты.
При повторном взведении датчика с вращательным движением рабочего элемента стабильность ускорения срабатывания главным образом определяется условиями крепления концов пружины к валу и корпусу и взаимным расположением деталей. Критичные конструктивные параметры при повторных срабатываниях прибора приведены в таблица.
Критичные конструктивные параметры при повторных срабатываниях датчика
|
Параметр |
1 |
2 |
3 |
4 |
|
Влияние угла α2 = 0º (угол отклонения от 90º контакта фиксатора к рычагу) (рис. 2) |
Влияние параметра величины смещения пружины относительно вала, в направлении стрелки (рис. 3) |
|||
|
Относительная погрешность срабатывания, % |
1 |
3 |
2 |
Менее 1 |
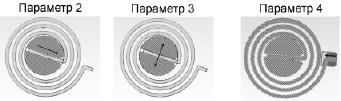
Рис. 3. Смещения пружины относительно вала датчика
Диаграмма влияния различных факторов (см. табл. 1) на погрешность срабатывания прибора показана на рис. 4.
Первый параметр влияет на погрешность срабатывания наиболее сильно (внутренний конец пружины не закреплен в пазу и может смещаться в направлении стрелки), поэтому целесообразно введение дополнительной контрольной операции при установке обоймы c плоской спиральной пружиной на вал крестовины для контроля данного смещения. Введение данной операции позволило, во-первых, существенно сократить временные затраты на анализ, сборку и разборку прибора при настройке ускорения срабатывания на центрифуге, во-вторых, повысить стабильность срабатывания прибора. Функции распределения срабатывания, рис. 5, при настройке для партии приборов до и после введения дополнительной контрольной операции. По кривой распределения видно существенное сокращение дисперсии ускорения срабатывания и уменьшение количества несоответствий при сборке и настройке.
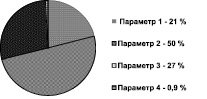
Рис. 4. Диаграмма влияния различных факторов на погрешность срабатывания прибора при повторных взведениях
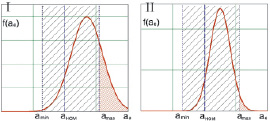
Рис. 5. I – функция распределения f(ae) ускорения срабатывания при настройке для партии приборов до введения дополнительной контрольной операции. II – функция распределения f(ae) ускорения срабатывания при настройке для партии приборов после введения дополнительной контрольной операции
Выводы
1. Математические модели, ориентированные на решение технологических задач, позволяют выявить критичные конструктивные параметры прибора, а также проследить связь: критичные конструктивные параметры – управляющие параметры технологического процесса – функциональная характеристика прибора.
2. Определение критичных конструктивных параметров и применение математических моделей эффективно и целесообразно, так как позволяет разработать рекомендации по улучшению технологических процессов и сократить время изготовления приборов и повысить стабильность их настройки.
Рецензенты:
Чечулин Ю.Б., д.т.н., профессор кафедры детали машин Института фундаментального образования Уральского федерального университета имени первого Президента России Б.Н. Ельцина, г. Екатеринбург;
Паршин В.С., д.т.н., профессор, заведующий кафедрой «Металлургические и роторные машины» Механико-машиностроительного института Уральского федерального университета имени первого Президента России Б.Н. Ельцина, г. Екатеринбург.
Работа поступила в редакцию 17.10.2013.



