В настоящее время для учащихся старшего школьного возраста одним из наиболее эффективных средств выявления способностей и уровней одаренности, а также развития интеллектуальных и творческих способностей являются подготовка и участие в предметных олимпиадах [4]. Среди всех школьных предметов можно выделить информатику как наиболее динамичный предмет, т.к. содержание олимпиадных задач по информатике постоянно изменяется. Следует отметить, что областные и региональные олимпиады по информатике традиционно являются олимпиадами по программированию, а школьные, а иногда и городские олимпиады – это олимпиады по ИКТ.
Проведенные нами опросы учителей информатики школ Волгоградской области показывают, что главную роль при подготовке школьников к олимпиадам по данному предмету занимают задачи. Анализ задач для олимпиад по информатике (программированию) в контексте содержания показал, что они включают задачи по сортировке и перебору данных, динамическому программированию, моделированию, оптимизации, длинной арифметике, линейному и двоичному поиску, жадным алгоритмам, рекурсии, теории графов, комбинаторике и по работе с данными строкового и файлового типов [2].
Многолетний опыт подготовки школьников к олимпиадам по программированию в Волгоградской области показывает, что в качестве основы для проведения занятий целесообразно использовать не отдельные задачи, а комплексные системы задач. Разнообразные наборы задач, входящих в системы задач для подготовки к олимпиадам по информатике, позволяют:
1) постепенно усложнять изучаемый материал;
2) поэтапно увеличивать объем работы;
3) повышать уровень самостоятельности учащихся;
4) привлекать элементы теории для решения познавательных задач;
5) обучать способам рассуждения (как по образцу, так и самостоятельно) с учетом принципа вариативности задач;
6) формировать важнейшие характеристики творческих способностей: беглость мысли (количество идей, возникающих за единицу времени), гибкость ума (способность переключаться с одной мысли на другую), оригинальность (способность находить решения, отличающиеся от общепринятых); любознательность (чувствительность к проблемам в окружающем мире), умение выдвигать и разрабатывать гипотезы.
При построении систем задач мы учитываем требования, определяющие педагогическую целесообразность их использования [1]: дидактические, отражающие соответствующие традиционные и специфические принципы обучения; и методические, учитывающие особенности информатики как учебного предмета и науки. При подготовке к олимпиадам по информатике мы выделили следующие требования к системам задач:
1) ключевая задача (наличие задач, сгруппированных в узлы вокруг объединяющих центров – задач, в которых рассматриваются факты или способы деятельности, применяемые при решении других задач и имеющие принципиальное значение для усвоения предметного содержания);
2) связность (возможность графически представить совокупность задач связным графом, в узлах которого ключевые задачи, выше них – подготовительные и вспомогательные, ниже – следствия, обобщения и так далее);
3) целевая достаточность (наличие достаточного количества задач для тренировки в классе и дома, аналогичных задач для закрепления метода решения, задач для индивидуальных и групповых заданий разной направленности, задач для самостоятельной (в том числе исследовательской) деятельности учащихся, задач для текущего и итогового контроля с учетом запасных вариантов и так далее);
4) психологическая комфортность (система задач учитывает наличие разных темпераментов, типов мышления, видов памяти).
На первых этапах подготовки к олимпиадам по информатике мы конструировали системы задач эмпирическим путем, но в дальнейшем мы пришли к тому, что процесс создания систем задач должен включать в себя следующие этапы: аналитический (анализ содержания учебного материала и требований стандарта, формулирование целей и установление их взаимного соответствия, отбор содержания), проектировочный (выбор методов и методических приемов, определение форм представления учебного материала, способов его подачи) и технологический (техническое создание систем задач в соответствии с предъявляемыми требованиями).
По теме «Техника программирования» нами разработаны системы задач по программированию разветвляющихся и циклических вычислительных процессов, системы задач для работы с одномерными и двумерными массивами, для обработки строк символов, для изучения рекуррентных алгоритмов, алгоритмов длинной арифметики и динамических структур данных, а по теме «Алгоритмы, методы и принципы решения задач» − системы задач для изучения алгоритмов линейного и двоичного (бинарного) поиска, алгоритмов сортировки информации, перебора (перестановки) данных, динамического программирования, алгоритмов работы с графами.
Приведем пример системы задач для изучения алгоритмов поиска информации, которая состоит из задач, построенных путем модификации условия или требования ключевых задач. При описании системы используются следующие обозначения [3]: У (условие) – задан массив переменной длины, Б (базис) – умение просматривать весь массив (с первого до последнего элемента), Т (требование) – найти элементы массива по заданным условиям, С (способ) – просмотреть весь массив и отпечатать элементы, удовлетворяющие заданному условию.
Задача 1. В одномерном массиве A(N) (N≤100) найти все положительные элементы (ограничение условия).
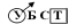
Задача 2. В одномерном массиве A(N) (N ≤ 100) найти все четные элементы (ограничение условия).
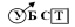
Задача 3. В одномерном массиве A(N) (N ≤ 100) найти все четные положительные элементы (получена из предыдущей добавлением в условие).

Задача 4. В одномерном массиве A(N) (N≤100) найти все четные положительные элементы с индексами, кратными 3 (получена из предыдущей добавлением в условие).
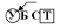
Задача 5. В одномерном массиве A(N) (N ≤ 100) увеличить в два раза все четные положительные элементы (получена из задачи 4 путем изменения требования).
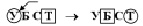
Задача 6. В одномерном массиве A(N) (N ≤ 100) возвести в квадрат все элементы, попадающие в интервал от –2 до 5 (получена из задачи 4 путем изменения требования).
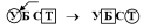
В процессе апробации разработанных нами систем задач была создана методика подготовки к олимпиадам по информатике на основе использования систем задач, которая построена с учетом специфик целевого (система целей – обучение с использованием системы задач), содержательного (дидактические единицы содержания, требующие отображения в системах задач) и процессуального (информации, определение видов, форм и способов подачи учебной информации в соответствии с особенностями методического стиля педагога) компонентов методической системы учителя информатики, реализуемых в системах задач.
Данная методика используется преподавателями Лицея при факультете довузовской подготовки ФГБОУ ВПО «Волгоградский государственный технический университет» при подготовке школьников к олимпиадам по информатике с 2003 и по настоящее время.
Многолетние наблюдения за школьниками, участвующими в процессе подготовки к олимпиадам по информатике показали, что использование систем задач, кроме подготовки к олимпиадам, еще влияет на развитие одаренности [5]. Поэтому в процессе педагогического исследования нами была разработана трехстадийная модель формирования одаренности в условиях подготовки школьников к олимпиадам по информатике, при построении которой мы ориентировались на то, что на каждой из стадий подготовки к олимпиадам учащиеся непосредственно участвуют в процессе формирования своей одаренности. Первая стадия является стадией самоопределения (самоидентификации одаренности) школьника, вторая – стадией определения границ своей одаренности, на третьей стадии происходит осознание, каким образом можно самостоятельно участвовать в процессе формирования своей одаренности. Данная модель является теоретической основой для проведения нами дальнейшей методической работы.
Содержание подготовки регламентирует выбор средств и форм работы, при этом для каждой стадии формирования одаренности в качестве средства выбраны системы задач по формированию знаний и умений школьника, по прогнозированию и формированию одаренности.
Эта стадийная модель внесла коррективы в содержательный и процессуальный компоненты разработанной нами методики подготовки к олимпиадам по информатике на основе использования систем задач. Сконструированные системы задач становятся основой для разработки индивидуальных образовательных траекторий для каждого ученика, что приводит к формированию одаренности учащихся путем развития способностей учащихся и реализации их личностного творческого потенциала. Методика стала стадийной, обеспечивая таким образом разноуровневость индивидуальных образовательных траекторий и трехэтапность процесса подготовки к олимпиадам по информатике и формирования одаренности при использовании комплексов систем задач и сочетании очной и дистанционной форм обучения.
Рецензенты:
Смыковская Т.К., д.п.н., профессор кафедры теории и методики обучения математике и информатике, ФГОУ ВПО «Волгоградский социально-педагогический университет», г. Волгоград;
Петрова Т.М., д.п.н., профессор кафедры теории и методики обучения математике и информатике, ФГОУ ВПО «Волгоградский социально-педагогический университет», г. Волгоград.
Работа поступила в редакцию 08.10.2013.



