В настоящее время во всем мире активно практикуется метод реабилитации, основанный на использовании физических упражнений в лечебных целях с помощью специальных аппаратов и приборов. Этот метод называется «Механотерапия», целью его является улучшение подвижности в суставе, восстановление максимально возможного объема движений в нем, тренировка мышц, улучшение кровообращения и микроциркуляции в тканях сустава [2].
Одним из главных направлений в реабилитации является разработка суставов. Существует большое количество различных тренажеров, методик и реабилитационных систем, которые позволяют заниматься реабилитацией конечностей, при этом управление аппаратами для разработки суставов максимально упрощено и не требует специальных знаний [4; 6; 7; 8; 9]. В настоящее время наибольшее распространение получили двухзвенные системы с одним активным шарниром. Такие устройства имеют ограниченные функциональные возможности, с целью их расширения появились трехзвенные конструкции аппаратов с несколькими активными шарнирами. Трехзвенная система может иметь пассивный коленный шарнир и голеностопный шарнир, перемещающийся поступательно.
В большинстве случаев тренажеры представляют собой системы для пассивной реабилитации, которые лишь сгибают и разгибают сустав в пределах заданного угла. При этом недостаточное внимание уделяется разработке и исследованию аппаратов, воздействующих на нужные группы мышц в определенные фазы движения сустава, тем самым навязывается правильный стереотип ходьбы и тренируются мышцы, необходимые для правильной походки. В данной статье рассматривается исследование заданного движения трехзвенного механизма с активными тазобедренным, коленным и голеностопным суставами, работа которого осуществляется в сопряжении с основными принципами движения нижней конечности человека. Применение таких активных элементов существенно повышает эффективность реабилитационных мероприятий.
Переход к цифровому управлению приводит к появлению дискретного управляемого движения механизма. Целью данного исследования является изучение закономерностей дискретного управляемого движения трехзвенного механизма с тремя активными шарнирами. Для достижения поставленной цели необходимо разработать математическую модель движения трехзвенника, получить результаты исследования, провести сравнительный анализ с экспериментальными данными.
Описание трехзвенного механизма
В работе рассматривается устройство для реабилитации нижних конечностей человека после травм, которое состоит из неподвижного основания 1, стола 2, штанг 3–5, соединенных между собой приводами вращательного движения 6–8, фиксаторов 9–13, которые фиксируют ногу человека, привода вращательного движения 14, для регулировки положения тела, червячного редуктора 15.
Устройство работает следующим образом.
Нога человека удерживается в механизме фиксаторами 9–13. Приводом 14 регулируется угол наклона тела пациента. Приводы 6–8 передают движение ноге пациента.
Переход к цифровому управлению приводит к появлению дискретного управляемого движения механизма.
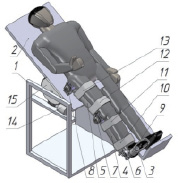
Рис. 1. Конструкция аппарата для реабилитации нижних конечностей человека после травм
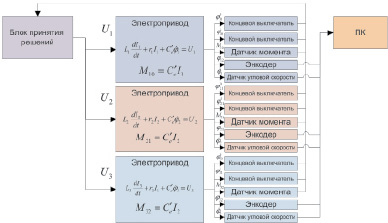
Рис. 2. Система автоматического управления аппаратом для реабилитации нижних конечностей человека после травм
Для устройства разработана система автоматического управления, которая представляет собой комплекс, включающий в себя:
1) пары концевых датчиков, датчиков моментов, датчиков угловых скоростей, датчиков углов поворота;
2) блок электроприводов;
3) блок принятия решений;
4) персональный компьютер.
Предложенная система управления устройством построена на базе микроконтроллеров серии Atmega, которые реализуют алгоритмы цифрового компаратора и интеллектуального регулятора. Пары концевых выключателей образуют релейную систему управления, направленную на повышение безопасности конструкции. Выбор такой многоканальной системы управления обусловлен необходимостью предотвращения возможных травм пациента при выполнении упражнений на устройстве.
Моделирование движения трехзвенного механизма
Исследуем режим работы трехзвенного механизма, при котором шарнир O3 движется поступательно. Такой принцип движения используется во многих существующих аппаратах для разработки суставов [1; 4].
Для получения результатов математического моделирования будем использовать следующую систему дифференциальных уравнений, описывающих движение рассматриваемого механизма [9]:
 (1)
(1)
В САУ аппаратом энкодеры измеряют относительные углы, определяемые по формулам φ10 = φ1 – φ0, φ21 = φ2 – φ1, φ32 = φ3 – φ2.
Для получения временных зависимостей крутящих моментов зададим законы изменения абсолютных углов звеньев:
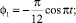
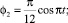
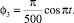 (2)
(2)
Углы φi изменяются в диапазоне 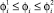 .
.
 ,
,  – это предельные значения соответствующих углов.
– это предельные значения соответствующих углов.
В результате расчетов получены временные характеристики идеальных управляющих моментов, точно обеспечивающих заданные законы изменения абсолютных углов звеньев механизмах (2).
а 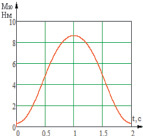 б
б 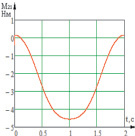 в
в 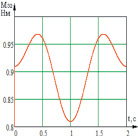
Рис. 3. Временные характеристики изменения идеальных моментов звеньев системы: а – временная характеристика изменения момента M10 звена 1; б – временная характеристика изменения момента M21 звена 2; в – временная характеристика изменения момента M32 звена 3
Для осуществления цифрового (дискретного) управления трехзвенным механизмом посредством полученных моментов, зададим их ступенчато, причем время дискретизации будем изменять в диапазоне 0,005 ≤ Δt ≤ 0,05 c. Получим следующие зависимости изменения углов звеньев от времени:
а 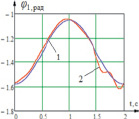 б
б 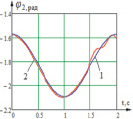 в
в 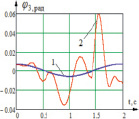
Рис. 4. Временные диаграммы изменения углов звеньев системы при подаче моментов M10, M21, M32: 1 – идеальная характеристика, 2 – полученная при подаче момента M10 с шагом дискретизации Δt = 0,05 c; а – диаграмма изменения угла φ1 звена 1; б – диаграмма изменения угла φ2 звена 2; в – диаграмма изменения угла φ3 звена 3
Как видно из графиков рис. 3, при подаче такого вида сигнала звенья системы не выходят на заданные углы (максимальная абсолютная ошибка угла φ1 составляет ξ1 = 5,8 %, для угла φ2 – ξ2 = 5,7 %), особенно значительны отклонения угла φ3 (ξ3 = 99 %), а также имеют место колебательные процессы, которые недопустимы при проектировании такого рода механизмов.
Попробуем улучшить результат, подавая моменты со временем дискретизации Δt = 0,025 c.
Подавая таким образом моменты, мы получили диаграммы изменения углов звеньев 1 и 2, которые соответствуют заданным законам, угол звена 3 при Δt = 0,025 c имеет нестабильный колебательный характер и требует уменьшения периода дискретизации управляющих моментов до Δt = 0,005 c (рис. 5).
а 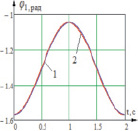 б
б 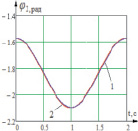 в
в 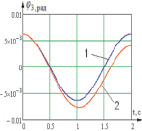
Рис. 5. Временные диаграммы изменения углов звеньев системы при подаче управляющих сигналов: 1 – идеальная характеристика, 2 – полученная при подаче дискретного сигнала; а – диаграмма изменения угла φ1 звена 1 при подаче момента M10 с шагом дискретизации Δt = 0,025 c; б – диаграмма изменения угла φ2 звена 2 при подаче момента M21 с шагом дискретизации Δt = 0,025 c; в – диаграмма изменения угла φ3 звена 3 при подаче момента M32 с шагом дискретизации Δt = 0,005 c
Таким образом мы получили угловые изменения звеньев системы с минимальной ошибкой, которая составляет для углов φ1 и φ2 ξ2 = 0,5 % для угла φ3 – порядка 25 %.
Заключение
В работе предложена конструкция аппарата для реабилитации нижних конечностей человека, оснащенного тремя управляемыми электромеханическими приводами, движение которого имитирует движение ноги человека. Приведена математическая модель, позволяющая исследовать управляемое движение устройства численным методом.
Описан принцип работы устройства и приведена система автоматического управления, представляющая собой многоканальную систему, выбор которой обусловлен необходимостью обеспечения заданного движения звеньев системы с минимальными отклонениями, а так же предотвращения возможных травм пациента при выполнении упражнений на устройстве. Приведенные закономерности могут быть применены при проектировании различных реабилитационных устройств.
Рецензенты:
Кобелев Н.С., д.т.н., профессор, заведующий кафедрой теплогазоснабжения и вентиляции, ЮЗГУ, г. Курск;
Игнатенко Н.М., д.т.н., профессор, заведующий кафедрой общей и прикладной физики, ЮЗГУ, г. Курск.
Работа поступила в редакцию 20.09.2013.


