Создание радиоэлектронных средств (РЭС) с учетом влияния температур усложняется на текущий момент следующими факторами [1–5]:
1) непрерывным увеличением и усилением температурных режимов при использовании РЭС;
2) случайностью разброса теплофизических свойств;
3) трудностями конструируемых изделий, состоящих из большого числа разных элементов;
4) большим количеством эксплуатационных режимов приборов.
Источниками теплоты в РЭС могут быть как отдельные радиоэлементы, так и электрические устройства. Они потребляют электроэнергию, которая превращается в другие виды энергии – механическую, электромагнитную, тепловую и т.д. Иначе говоря, определенный процент энергии, используемой конструктивными элементами РЭС и радиоэлементами, превращается в полезные сигналы, все же остальное переходит в тепло.
Различные условия эксплуатации РЭС усложняют диапазон воздействий. Чаще всего эти воздействия крайне жесткие, что крайне негативно влияет на эксплуатацию проектируемых устройств. Учитывая вышесказанное, необходимо точно оценить температурные условия, в которых будет эксплуатироваться изделие, и, только исходя из полученных данных, проводить процесс проектирования.
Математические модели тепловых процессов при стационаре и нестационаре
Метод электротепловой аналогии (ЭТА) позволяет проводить высокоточные исследования тепловых полей в конструкциях РЭС, учитывая при этом условия охлаждения и особенности конструктивного построения. Данный метод дает возможность представить проходящие в конструкциях РЭС тепловые процессы в виде электрической схемы, которая затем анализируется с помощью отработанного на сегодняшний день математического аппарата по численному анализу электрических цепей. Такой алгоритм работы математически выглядит как замена в частных производных дифференциальных уравнений, изображающих температурные процессы в аппаратуре, уравнениями в конечных разностях. Рассмотрим данный подход на примере дифференциального уравнения Фурье‒Кирхгофа в аспекте решения стационарной задачи в применении к твердым изотропным телам. В декартовой системе координат данное уравнение выглядит следующим образом:
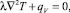(1)
где T – температура; λ – коэффициент теплопроводности материала изотропного твердого тела;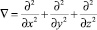 
– оператор Лапласа; qV – удельная мощность внутренних источников энергии.
Запись в конечных разностях уравнения (1) основана на допустимости изменения процесса с непрерывного на дискретный, т.е.
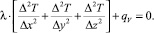(2)
С целью наглядности последующих рассуждений произведем разбиение условно твердого тела на ряд объемов (параллелепипедов), имеющих, как показано на рис. 1, а, размеры Δx, Δy, Δz. Рассмотрим совокупность элементарных объемов в направлении оси OX. С этой целью произведем выделение объема V0 и соседствующих с ним объемов V1, V2 (рис. 1, б) в твердом теле (рис. 1, а). Температурам в серединах соответствующих условно изотермических объемов дадим условное обозначение T0, T1, T2.
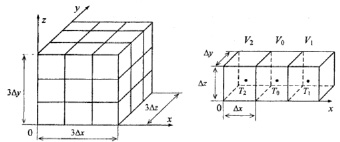
Рис. 1. Условно разбитое ортогональными плоскостями (а) твердое тело на элементарные объемы, а также выделенная совокупность элементарных объемов вдоль оси OX (б)
В объеме V0 содержатся внутренние источники энергии, имеющие удельную мощность q0. В таком случае составляющая по оси OX (с использованием разности вперед) для объема V0 уравнения (2.2) примет следующий вид:
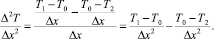(3)
По аналогии рассмотрим совокупность объемом по осям OY и OZ (рис. 2). Для составляющий уравнения (2) запишем разностные аналоги вдоль осей OY и OZ соответственно:
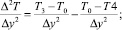(4)
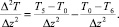(5)
Уравнение (2), учитывая выражения (3), (4) и (5), можно представить в следующем виде:
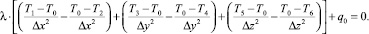(6)
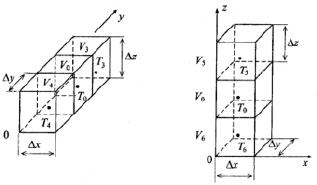
Рис. 2. Совокупности элементарных объемов вдоль осей ОY и OZ
Произведем умножение обеих частей уравнения (6) на объем параллелепипеда
V0 = Δx∙Δy∙Δz,
получим:
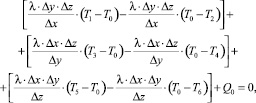(7)
где Q0 = q0∙Δx∙Δy∙Δz – рассеиваемая в элементарном объеме V0 тепловая мощность.
Введем следующие обозначения:
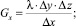
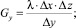
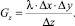
Указанные параметры Gx, Gy, Gz имеют физический смысл, а также размерность (Вт/К) тепловых проводимостей между соседними элементарными объемами твердого тела по осям OX, OY и OZ соответственно. С учетом введенных параметров, уравнение (7) будет выглядеть следующим образом:
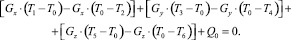(8)
Уравнение (8) является конечно-разностным. Оно описывает теплообмен в элементарном объеме твердого тела, имеет аналогом записанное на основе 1-го закона Кирхгофа уравнение для суммы токов нулевого узла электрической цепи (рис. 3).
Алгоритм ввода конструкции
Для проведения расчета конструкции необходимо предварительно ввести ее параметры в запоминающее устройство ЭВМ. С этой целью были разработаны соответствующие алгоритмы, поддерживающие 3 варианта ввода конструкции:
1) ручной ввод конструкции;
2) импорт конструкции из компьютерной программы АСОНИКА-В;
3) импорт конструкции из промежуточного формата IGES программ 3D-моделирования.
При ручном вводе конструкции пользователю необходимо самостоятельно вводить название элементов конструкции и его координаты: X, Y, Z (левый ближний нижний угол) и X, Y, Z (правый дальний верхний угол).
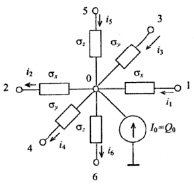
Рис. 3. Фрагмент электрической схемы, который моделирует процессы теплопередачи в элементарном объеме V0
Для импорта конструкции из компьютерной программы АСОНИКА-В пользователь ЭВМ, открыв конструкцию, выбирает в меню «Сервис» пункт «Export geometry…», после чего данные записываются в текстовый файл.
Импорт данных из компьютерной программы IGES аналогичен импорту из подсистемы АСОНИКА-В.
В ходе исследований был проведен эксперимент, целью которого было выяснение времени, затраченного на ввод конструкции с различным количеством элементов при помощи трех вышеприведенных способов, а также выяснение наиболее эффективного способа ввода конструкции. Результаты эксперимента представлены на рис.4.
Таким образом, можно сделать вывод, что наиболее эффективным способом ввода является ввод из формата IGES. Если такой возможности нет, то придется выбирать между ручным вводом и вводом в программе АСОНИКА-В. Несмотря на то, что ручной ввод оказывается более быстрым, в пользу ввода через программу АСОНИКА-В говорит тот факт, что она является более наглядной и сразу же представляет пользователю 3D-модель конструкции, тогда как ручной ввод предполагает простое введение координат.
Алгоритм разбиения конструкции на элементарные объемы для автоматизированного синтеза моделей тепловых процессов произвольных конструкций
Для автоматизированного синтеза моделей тепловых процессов произвольных конструкций РЭС по результатам проведенных исследований предложено разбивать конструкцию на элементарные объемы – кубики, также на кубики разбивается воздушное пространство внутри конструкции. А далее учитываются все возможные виды тепловых взаимодействий между этими элементарными объемами. При этом учитывается, какому элементу конструкции принадлежит кубик.
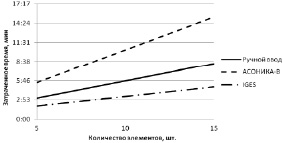
Рис. 4. Зависимость затраченного на ввод конструкции времени от способа ввода и количества элементов
Схема разработанного алгоритма разбиения конструкции произвольного типа на кубики представлена на рис. 5. Рассмотрим алгоритм более подробно.
Блок 1. Задается цикл по оси X, в котором конструкция просматривается по длине с шагом, равным стороне кубика.
Блок 2. Задается цикл по оси Y, в котором конструкция просматривается по глубине с шагом, равным стороне кубика.
Блок 3. Задается цикл по оси Z, в котором конструкция просматривается по высоте с шагом, равным стороне кубика.
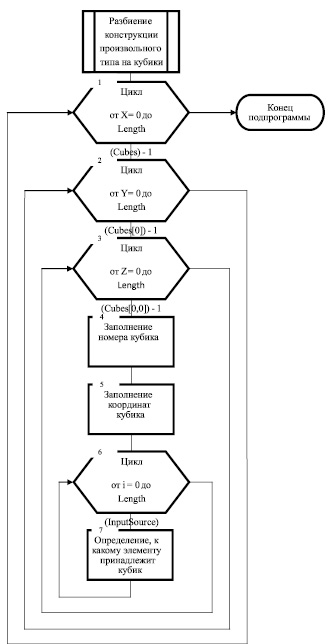
Рис. 5. Схема алгоритма разбиения конструкции на элементарные объемы
Блок 4. Присвоение кубикам порядкового номера в массиве кубиков. Нумерация начинается с левого ближнего нижнего угла конструкции и заканчивается в правом дальнем верхнем угле конструкции.
Блок 5. Заполнение координат кубика. В трехмерный массив заносятся координаты левого ближнего нижнего и правого дальнего верхнего углов каждого кубика.
Блок 6. Задается цикл, в ходе которого производится перебор всех элементов конструкции.
Блок 7. Определяется, к какому элементу конструкции принадлежит кубик. Кубик может также принадлежать воздуху внутри конструкции. Производится анализ координат кубика на предмет их вхождения в координаты элемента конструкции.
Алгоритм прорисовки конструкции
В ходе проведенных исследований по построению тепловой модели произвольной конструкции возникла необходимость в предварительном просмотре результатов разбиения конструкции на кубики. Необходимо определить, насколько корректно конструкция разбилась на элементарные объемы, например, не пропали ли детали слишком маленького размера, не слились ли две детали в одну и т.д.
С этой целью был разработан алгоритм двухмерной визуализации трехмерного объекта путем его разделения на слои. Данный алгоритм поддерживает возможность выбора слоя конструкции (координаты по оси Z). Также имеется возможность определения и вывода на дисплей ЭВМ названия элемента, содержащегося в данном квадратике, а также внутренний уникальный номер кубика.
Выводы
В ходе выполнения данной работы разработаны: алгоритм ввода конструкции, алгоритм разбиения конструкции на элементарные объемы для автоматизированного синтеза моделей тепловых процессов произвольных конструкций, алгоритм прорисовки конструкции, алгоритмы автоматизированного синтеза моделей тепловых процессов произвольных конструкций РЭС для стационарного и нестационарного режимов, структура промежуточного файла между препроцессором и расчетным ядром, алгоритм вывода результатов расчета при стационарном и нестационарном режиме.
Исследование осуществлено в рамках Программы фундаментальных исследований НИУ ВШЭ в 2013 году, при финансовой поддержке Министерства образования и науки Российской Федерации, гранта Президента РФ для государственной поддержки молодых российских ученых № МК-7052.2012.8.
Рецензенты:
Малютин Н.В., д.т.н., профессор, заместитель Генерального директора по инновациям, ОАО «НПЦ «САПСАН», г. Москва;
Кофанов Ю.Н., д.т.н., профессор, заместитель генерального директора ООО «Научно-технический центр «Наномодель», г. Ковров.
Работа поступила в редакцию 20.09.2013.