Совокупность оптических методов визуализации структуры биологических тканей, использующих различные эффекты взаимодействия света с рассеивающими средами, в настоящее время носит название оптической томографии (ОТ) [1]. Одним из наиболее перспективных методов ОТ является диффузионная оптическая томография (ДОТ) – метод исследования биологических тканей на глубину до 10–15 см, основанный на регистрации и последующем анализе динамики изменения интенсивности одиночного импульса лазерного излучения ближнего инфракрасного (ИК) диапазона в процессе многократного рассеяния (диффузии фотонов) внутри биологической ткани.
На сегодняшний день не все научно-технические проблемы ДОТ решены, и диффузионные томографы не выпускаются серийно. Тем не менее один оптический маммограф, как первый опытный образец, проходящий уже этап клинических испытаний, сегодня известен – маммограф «CTLM» фирмы «Imaging Diagnostic Systems, Inc.» (США) [2]. Однако, как первый образец он достаточно громоздкий и дорогостоящий.
Целью данной работы является попытка упрощения процесса регистрации неоднородностей в биологических тканях, т.е. частичного разрешения одной из ключевых проблем ДОТ.
Модель распространения фотонов в сильно рассеивающей среде
Для получения временных функций рассеяния точки (ВФРТ) в данной работе используется модель капли – единичного импульса излучения с заданным количеством фотонов, попадающего в объект около поверхности и диффундирующего внутри него [9]. Она позволяет достаточно точно описать экспериментально полученные данные [4, 8] как для однородного, так и для неоднородного случаев и базируется на численном решении уравнения переноса излучения (УПИ) в диффузионном приближении с граничным условием третьего рода (Робина).
Согласно диффузионному приближению к УПИ [6], распределение фотонов в объеме моделируемого трехмерного конечного объекта в последовательные моменты времени описывается как:
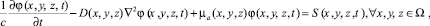
где C – скорость света в среде, x, y, z – координаты всех точек конечной моделируемой области, включающей в себя внутреннюю часть моделируемого объекта (Ω), его границу (∂Ω), источник излучения (q), детекторы и окружающую объект среду; D(x, y, z) и μa(x, y, z) – соответственно коэффициент диффузии и коэффициент поглощения в точках с координатами x, y, z. S(x, y, z, t) – функция источника фотонов, представляющая собой зависимость количества фотонов, вводимых в моделируемый объект Ω в точке q границы ∂Ω от момента времени t. Скорость света в среде c вычисляется из
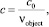
где c0 – скорость света в вакууме и νobject – относительный коэффициент преломления моделируемого объекта Ω и его границы ∂Ω. Отметим, что в модели вместе с параметром νobject используется параметр νmedium – относительный коэффициент преломления окружающей объект среды (в случае воздуха νmedium = 1). Коэффициент диффузии [6] находится как:
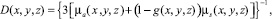
где μs(x, y, z) и g(x, y, z) – коэффициент рассеяния и параметр анизотропии в точках с координатами x, y, z соответственно.
Граничное условие Робина используется для описания потока фотонов на границе [5] моделируемого объекта Ω:
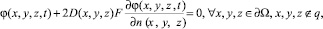
где n(x, y, z) – направление внешней нормали к границе ∂Ω в точке с координатами x, y, z ; F – коэффициент френелевского отражения [5], вычисляемый как:
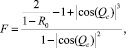
где R0 и Qc коэффициенты, соответственно равные:
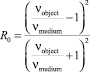и 
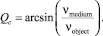
Описанная модель реализована на графическом языке программирования «G» среды разработки и платформы для выполнения программ LabVIEW. Неявная разностная схема построена по семиточечному шаблону. Начальное приближение функции φ(x, y, z, t) во всех узлах сетки генерируется с учетом позиции источника фотонов и количества фотонов, испускаемых в течение одиночного импульса. В качестве критерия окончания итерационного процесса использовано достижение заданной точности (критерий подгонки). Результаты моделирования распределения фотонов в однородном и неоднородном цилиндрическом объекте показаны на рис. 1.
а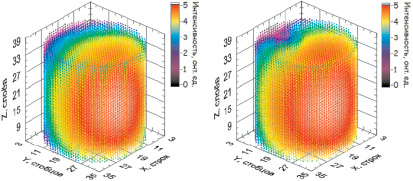
б
Рис. 1. Распределение фотонов в однородном (а) и неоднородном (б) цилиндрических объектах через 0,75 нс после испускания импульса
Индекс неоднородности
В связи со сложностью решения обратной задачи в ДОТ и высокими требованиями к производительности вычислений в данной работе предлагается обратить внимание на возможность прямой регистрации неоднородностей. Одним из способов такой регистрации является использование специального индекса, вычисляемого на основе ВФРТ.
В работах [3, 7, 9] вводится понятие индекса неоднородности – Hi(t), который представляется как зависимость от времени стандартного отклонения интенсивности излучения от его средних значений для N-го количества детекторов. Hi(t) обладает достаточно высокой информативностью. В однородном случае он стремится к нулю, а в неоднородных (поглощающая неоднородность) – к параллельным прямым. Минимум наблюдается, когда поглощающая неоднородность располагается рядом с источником излучения. Таким образом, индекс неоднородности позволяет легко отличать однородный случай от различных неоднородных, но указать позицию неоднородности он не может. В связи с этим предлагается новый подход к вычислению индекса, главным принципом которого является использование только поздно пришедших фотонов (ППФ), т.е. только конечных частей ВФРТ.
Индекс неоднородности можно вычислять следующим образом: сначала для ППФ каждой ВФРТ определить среднюю плотность потока фотонов, затем нормировать её и на основании полученных данных построить двумерный график её зависимости от угла между световодом источника излучения и световодом детектора соответствующего ВФРТ.
Обозначим ППФ ВФРТ как R(α, t), где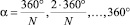 
– углы к оси падающего излучения, под которым располагаются детекторы; N – количество детекторов, 
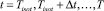– дискретные моменты времени, с шагом Δt; T – максимальное время, прошедшее с момента падения импульса на объект, в течение которого попавшие на детектор фотоны регистрируются (чаще всего 5–7 нс), Tisot – минимальное время, прошедшее с момента падения импульса на объект до момента, когда все детектируемые фотоны можно считать поздно пришедшими (чаще всего 2–3 нс). Далее, отнеся количество ППФ R(α, t), попавших на детектор α к площади поверхности детектора Sa и времени Δt, получаем величину плотности потока фотонов на детекторе P(α, t):
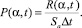
Находим среднюю плотность потока ППФ на α-м детекторе:
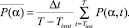
И, наконец, нормируя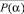 
, получаем индекс неоднородности H(α), представляющий собой зависимость средней плотности ППФ от угла между световодом источника излучения и световодом детектора соответствующего ВФРТ.
Результаты исследования и их обсуждение
Предложенный подход к вычислению индекса неоднородности, как и модель распространения фотонов в оптически мутной среде, был реализован в виде специализированного программного продукта в среде LabVIEW. Результаты его работы для одинаковых по размерам однородного и нескольких неоднородных модельных объектов показаны на рис. 2. В неоднородных случаях использовалась поглощающая неоднородность размером 30 % от диаметра моделируемого объекта, расположенная под углом 180° к оси падающего излучения на глубине 10 % от диаметра моделируемого объекта. Из рисунка следуют основные преимущества предлагаемого :
Ø В однородном случае он является прямой линией.
Ø В неоднородных случаях он представляет собой кривую, причем если неоднородность поглощающая, то у кривой будет четко выраженный глобальный максимум, если рассеивающая – глобальный минимум.
Ø Координата экстремума по оси H (в данном случае «Индекс неоднородности, отн. ед.») примерно характеризует:
- в случае поглощающей неоднородности – разницу между коэффициентами поглощения неоднородности и однородной части
- в случае рассеивающей неоднородности – разницу между коэффициентами рассеяния неоднородности и однородной части
Ø Координата экстремума по оси α (в данном случае «Угол, градусов») указывает угол между световодом источника излучения и световодом ближайшего к неоднородности детектора, т.е. примерное местоположение неоднородности.
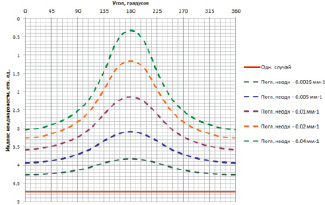
Рис. 2. Индекс неоднородности для однородного и пяти неоднородных цилиндрических объектов
Заключение и выводы
В данной работе описаны модель распространения фотонов в сильно рассеивающей среде, основанная на численном решении УПИ в диффузионном приближении с граничным условием Робина, и новый подход к прямой регистрации неоднородности в моделируемом объекте на основе вычисления, визуализации и анализа индекса неоднородности [3, 7, 9]. Предложенный подход отличается меньшим объемом вычислений, т.к. анализируются данные только о ППФ, и большей информативностью, т.к. он позволяет для всех несимметричных случаев непосредственно, без решения обратной задачи определить не только наличие или отсутствие, но и местоположение и примерные оптические свойства поглощающей или рассеивающей неоднородности в цилиндрических и сферических объектах в режиме реального времени.
Рецензенты:
Литовка Ю.В., д.т.н., профессор кафедры «Системы автоматизированной поддержки принятия решений», ФГБОУ ВПО ТГТУ, г. Тамбов;
Туголуков Е.Н., д.т.н., профессор кафедры «Техника и технологии производства нанопродуктов», ФГБОУ ВПО ТГТУ, г. Тамбов.
Работа поступила в редакцию 16.09.2013.