Разработка специализированных вычислителей на ПЛИС часто требует нахождения численного значения элементарных математических функций. Обычно для этого используются имеющиеся в стандартном пакете САПР мегафункции. Так, например, в САПР Quartus II фирмы «Альтера» [5], имеются мегафункции для вычисления основных математических функций, такие как altpf_exp, altpf_log. altpf_sincos. Эти мегафункции работают с данными, представленными согласно стандарту IEEE 754 в формате с плавающей точкой. Допускается использование вычислений с одинарной (1 бит знака, 8 бит – порядок, 23 бита – мантисса), двойной (1 бит знака, 11 бит – порядок, 52 бита – мантисса) и одинарной расширенной (1 бит знака, 31 – 52 мантисса) точностями.
Ниже приведена таблица, заимствованная из документации к САПР Quartus II, характеризующая аппаратные затраты и производительность мегафункции altpf_exp применительно к ПЛИС серии Stratix III.
Таблица 1
Параметры мегафункции altpf_exp
|
Точность |
Задержка (такты) |
Логические элементы |
Макс. частота работы, мГц |
|||
|
Таблицы перекодировок (ALUTs) |
Спец. регистры (DLRs) |
Модули ALMs |
18-битные DSP блоки |
|||
|
Одинарная |
17 |
631 |
521 |
445 |
19 |
275 |
|
Двойная |
25 |
4138 |
2022 |
2959 |
46 |
257 |
Согласно приведенным данным, время получения результата при одинарной точности составляет порядка 62 nS, а при двойной точности – порядка 98 nS.
На практике диапазон изменения аргумента заранее известен, и он, как правило, значительно уже, чем допускает мегафункция. Поэтому практический интерес представляет поиск более гибких решений, обеспечивающих получение требуемой точности вычисления при меньших аппаратных затратах и большем быстродействии.
Нахождение численного значения элементарных функций всегда сводится к вычислению некоторого степенного многочлена. Широко известные методы вычисления многочлена, такие как метод Горнера [2], методы с предварительной обработкой коэффициентов [4], хотя и позволяют ускорить вычисление многочлена, но по своей структуре фактически нацелены на последовательное, итерационное вычисление, свойственное классическим вычислительным машинам.
Применение ПЛИС позволяет произвольно синтезировать структуру вычислителя, широко используя распараллеливание процесса, что предполагает значительное сокращение времени получения результата. Одним из методов, позволяющих реализовать такую возможность, является метод БВЕ (Быстрое Вычисление Е-функций). Рассмотрим особенности применения этого метода на примере вычисления функции exp(x).
Алгоритм, описанный в [1], предполагает, что диапазон изменения аргумента удовлетворяет условию 0 < x0 < 0,25 и число верных разрядов результата n > 8. Расчетная разрядность аргумента для требуемого числа верных разрядов результата определяется выражением N = 2k+1, где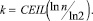 
Сгруппируем весовые коэффициенты расчетного аргумента
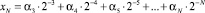
по степеням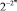 
:
(1)
где
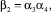
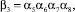
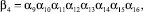
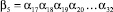
и так далее. В общем случае βv есть некоторое целое двоичное число, полная запись которого определяется выражением:
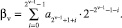
Используя выражение (1), функцию exp(xN) можно представить в следующем виде
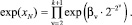(2)
Выражение (2) позволяет разбить вычислительный процесс определения численного значения функции exp(xN) на несколько параллельно выполняемых ветвей.
Вычисление каждой ветви выполняется с использованием ее разложения в ряд Маклорена:
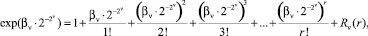(3)
причем число членов каждого разложения определяется выражением:
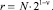(4)
Так, например, для вычисления функции с 12 верными разрядами имеем k = 4, N = 32,
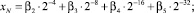
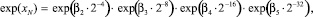
причем число членов в соответствующих разложениях ряда Маклорена определяется из условия (4) следующим образом: r = 16 для exp(β2∙2–4), r = 8 для exp(β3∙2–8), r = 4 для exp(β4∙2–16), r = 2 для exp(β5∙2–32).
Из приведенного примера видно, что чем больше в (3) значение v, тем меньше членов в соответствующем разложении, то есть тем проще реализация вычислителя.
На рис. 1 приведен граф вычислительного процесса, соответствующий выражению (2) для 12 верных разрядов результата.
Модуль BL_B2 реализует вычисление exp(β2∙2–4), модуль BL_B3 – вычисление exp(β3∙2–8), модуль BL_B4 – вычисление exp(β4∙2–16), а модуль BL_B5 – вычисление exp(β5∙2–32). Очевидно, что длина графа для каждого модуля будет определяться значением r. Так,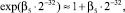 
что не требует выполнения каких-либо вычислений и сводится к перезаписи соответствующих разрядов аргумента в результат:
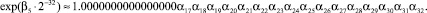
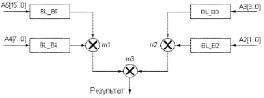
Рис. 1. Граф вычислительного процесса, соответствующий выражению (2) для 12 верных разрядов результата
Модуль BL_B3 реализует вычисление согласно выражению:
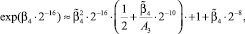
где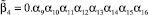 
– число < 1, и A3 = 1,5.
Граф процесса, реализованный в данном модуле, показан на рис. 2. Его реализация требует только двух умножителей. Очевидно, что графы, реализованные в модулях BL_B2 и BL_B3, имеют значительно более сложную структуру.
Результаты моделирования проекта в среде Quartus II приведены на рис. 3. Минимальное число верных разрядов результата равно 33, что значительно превосходит исходные требования (12 разрядов). Следовательно, для заданной точности такое решение является избыточным. Аппаратные затраты на реализацию вычислителя сведены в табл. 2.
Анализ полученных результатов показал, что основные затраты аппаратных ресурсов расходуются для реализации модулей BL_B3 и BL_B2. При этом на входах данных модулей соответственно действуют 2 и 4-разрядные аргументы, то есть возможное число выходных значений соответственно равны 4 и 16. В этом случае целесообразно отказаться от применения в этих модулях разложения в ряд Маклорена в пользу табличного выбора заранее рассчитанных результатов соответствующих аргументов.
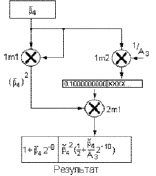
Рис. 2. Граф модуля BL_B3
Рис. 3. Результаты моделирования проекта в среде Quartus II
Таблица 2
Аппаратные затраты на реализацию метода БВЕ
|
Модуль |
ALUTs блоки |
18 бит DSP блоки |
|
BL_B5 |
0 |
0 |
|
BL_B4 |
26 |
11 |
|
BL_B3 |
72 |
26 |
|
BL_B2 |
271 |
56 |
|
Общие для рис. 1 |
622 |
139 |
Реализация такого подхода в среде Quartus II потребовала 49 ALUTs и 17 DSP блоков. При этом в модулях BL_B2 и BL_B3 использованы константы с 32 верными разрядами. Суммарное время вычисления не превосходит 30 nS. Минимальное число верных разрядов результата равно 31.
Следует отметить, что, так как константы в модулях BL_B2 и BL_B3 могут быть рассчитаны с произвольным числом верных разрядов, общая точность вычисления определяется процессами в модулях BL_B4 и BL_B5.
Расчеты показывают, что предельная точность вычисления в модуле BL_B5 по предложенному алгоритму соответствует максимальному значению аргумента и составляет 34 верных разряда результата. Предельная точность вычисления по алгоритму на рис. 2 для модуля BL_B4 составляет 37 верных разрядов. Эти цифры являются определяющими при выборе разрядностей констант в модулях BL_B2 и BL_B3.
Как было отмечено ранее, рассмотренный алгоритм позволяет вычислить значение функции при условии, что аргумент лежит в диапазоне 0 < x0 < 0,25. При больших значениях аргумента результат может быть получен с использованием выражения:
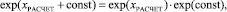(5)
где xРАСЧЕТ – расчетное значение аргумента из диапазона 0 < x0 < 0,25; exp(const) – заранее вычисленная константа.
Это потребует использования дополнительного умножителя и блока памяти с вычисленными значениями exp(const).
Наиболее просто решить задачу расширения диапазона изменения аргумента при реализации на ПЛИС можно в случае, если изменение аргумента лежит в диапазоне 0 ≤ x < ln(2) [3]. В этом случае результат при более широком диапазоне изменения аргумента сдвигается влево на величину s, равную неполному частному от деления действительного аргумента на ln(2):
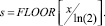
При таком подходе реализация выражения (5) потребует введения в устройство блока вычисления s, а сама функция ищется от нового аргумента xРАС, равного:
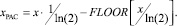
Полученный результат при помощи сдвигового регистра может быть сдвинут на s разрядов влево, либо представлен в показательной форме в виде порядка и мантиссы. При этом порядок – целое число, а мантисса всегда содержит один разряд целой части. Очевидно, что такой подход вносит в расчет дополнительную погрешность, обусловленную приближенностью значения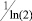 
. Для ее уменьшения желательно число верных разрядов констант выбирать большим числа верных разрядов аргумента, как минимум на один.
На рис. 4 приведена заимствованная из [3] структура блока подготовки данных, выделяющая из исходного аргумента порядок и новое расчетное значение аргумента, удовлетворяющее условию 0 ≤ x < ln(2). Ее реализация требует двух умножителей.
Для использования такого подхода модуль BL_B2 должен содержать все константы, удовлетворяющие условию 0 ≤ x < ln(2), что легко обеспечить на практике.
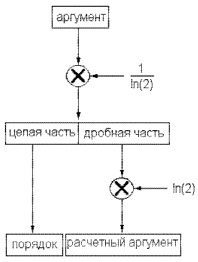
Рис. 4. Структура блока подготовки данных.
С использованием описанного подхода был разработан вычислитель для функции exp(x), формирующий на выходе порядок и мантиссу. Его основные параметры:
- исходный аргумент 4 разряда целой части + 33 разряда дробной части;
- разрядность порядка – 5 разрядов;
- разрядность мантиссы – 1 разряд целой части + 34 разряда дробной части;
- аппаратные затраты – 117 блоков ALUTs и 29 DSP блоков;
- максимальное время вычисления на ПЛИС Stratix III не превосходит 45 nS;
- минимальное число верных разрядов на выходе – 30 разрядов.
На рис. 5 приведены временные диаграммы, полученные в результате моделирования вычислителя в среде Quartus II фирмы Altera (A – аргумент, man – мантисса, por – порядок).
Рис. 5. Временные диаграммы, полученные в результате моделирования вычислителя
Из проведенных исследований следует вывод, что комбинация табличного и БВЕ методов делает возможным разработать вычислитель для функции exp(x), который при ограниченном диапазоне изменения аргумента позволяет реализовать устройство с меньшими аппаратными затратами и большим быстродействием. При увеличении точности вычисления достоинства предлагаемого метода становятся более ощутимыми.
Рецензенты:
Волков Н.Н., д.т.н., профессор Московского государственного технического университета им. Н.Э. Баумана (МГТУ им. Н.Э. Баумана), кафедра «Информационные системы и телекоммуникации», г. Москва;
Шевцов Д.А., д.т.н., профессор Московского авиационного института (Национального исследовательского университета), кафедры № 306 «Микроэлектронные электросистемы», г. Москва.
Работа поступила в редакцию 18.09.2013.