В промышленности процесс абсорбции применяется для разделения и осушки углеводородных газов. Увеличение масштабов производства при возросшем в настоящее время внимании к вопросам экологии и качеству готовой продукции требует дальнейшей разработки научно обоснованных и надежных методов расчета абсорбционной аппаратуры. Наиболее полное описание процессов, происходящих при массопередаче в системах «газ-жидкость», возможно на основе кинетических методов расчета. Но применение этих методов затруднено в связи с необходимостью определения коэффициентов массоотдачи и массопередачи [1-3]. Предлагаемый метод расчета кинетики изотермической абсорбции для многокомпонентных систем основан на уравнении массопередачи, которое получено в рамках нелокальной версии термодинамики (НВТ) [4]. Использование этого подхода позволяет частично устранить основную трудность, присущую кинетическим методам расчета.
Описание кинетики массообменного процесса на основе НВТ стало возможным в связи с тем, что установленный В.П. Майковым принцип дискретизации термодинамических параметров [4] позволяет внести в термодинамику время как существенный параметр. Рассмотрим кратко основные закономерности дискретизации термодинамических параметров. Приводимые ниже теоретические выводы не опираются на какие-либо модельно-механизменные представления и сохраняют в значительной степени термодинамический характер.
Принцип квантования термодинамических параметров явился следствием того, что естественная граница точности измерения количества теплоты (среднее значение теплового шума kT где k – константа Больцмана, k = 1,38∙10–23 Дж/К; T – термодинамическая температура, К) была принята в качестве минимального значения количества теплоты. Записав второй закон термодинамики в конечных приращениях
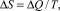 (1)
(1)
где ΔQ – количество теплоты, Дж; ΔS – приращение энтропии, Дж/К; и приравняв ΔQ = kT получим минимальное приращение энтропии
ΔS = k. (2)
Здесь и далее минимальные приращения параметров будут обозначаться значком Δ.
Используя величину ΔQ как минимальную энергию в соотношении неопределенностей энергия-время квантовой физики, можно получить характерный масштаб времени
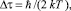 (3)
(3)
где ħ – постоянная Планка, ħ = 1,05∙10–34 Дж∙c.
Величина Δτ определяет размеры пространства, в котором устанавливается локальное термодинамическое равновесие и формируется температура как термодинамический параметр (для нормальных условий Δτ имеет порядок 10–14 c). Объем этого пространства для однородной изотропной среды составит
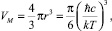 (4)
(4)
где 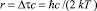 – характерный радиус взаимодействия, здесь с – скорость света в данной среде, м/с.
– характерный радиус взаимодействия, здесь с – скорость света в данной среде, м/с.
Далее этот объект будем называть макроячейкой. Так как макроячейка задает размеры пространства, в котором устанавливается термодинамическое равновесие, то для неё применимы соотношения равновесной термодинамики. Поэтому состояние макроячейки может быть охарактеризовано с помощью температуры, энтропии, массы количества частиц и других термодинамических параметров. Но эти параметры можно рассчитать лишь с конечной долей определенности. Возникающая неопределенность носит объективный характер и связана с тем, что макроячейки постоянно обмениваются между собой элементарными порциями количества теплоты ΔQ = kT.
Если макроячейка получает элементарную порцию количества теплоты ΔQ при P = const, то объем, температура и масса макроячейки изменяются на величину
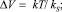 (5)
(5)
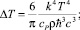 (6)
(6)
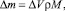 (7)
(7)
где kS – адиабатический модуль сжатия, н/м2; cP – мольная изобарная теплоемкость, Дж/(кмоль К); ρ – молярная плотность, кмоль/м3; M – молярная масса, кг/кмоль.
Выбор условия P = const вызван тем, что в состоянии динамического (флуктуационного) равновесия каждая отдельная макроячейка выступает лишь как область пространства, охваченная электромагнитным взаимодействием за время Δτ, т.е. макроячейка не является объемом, который был бы физически фиксирован в определенных границах.
Изменение массы макроячейки – элементарная масса Δm содержит меньше одной частицы. Это значит, что элементарную массу можно рассматривать только как квазичастицу, которая в данном случае является акустическим фононом. Этот акустический фонон и отвечает за перенос массы, тепла и импульса в данной среде.
Так как минимальная скорость распространения акустического фонона (квазичастицы) равна скорости распространения звука в данной среде (это можно доказать), то можно ввести еще один характерный радиус взаимодействия – это радиус упругих взаимодействий между макроячейками
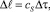 (8)
(8)
где cS – скорость звука в данной среде, м/с.
Известно, что уравнения массообмена, с помощью которых вводятся коэффициенты массопереноса, не имеют фундаментальной теоретической основы. Аппарат НВТ позволяет сформулировать основания такой теории.
Определим удельный равновесный мольный поток i-го компонента следующим образом
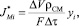 (9)
(9)
где ρСМ – молярная плотность смеси, кмоль/м3; yi – мольная доля компонента; F – поверхность, через которую проходит поток вещества, м2.
Поверхность F определяется как отношение характерного для упругих взаимодействий объема ΔV к характерному линейному размеру Δℓ. Тогда выражение для удельного равновесного потока для i-го компонента запишется следующим образом
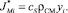 (10)
(10)
Если подставить значения скорости звука и плотности смеси для идеальногазовых условий, то получим следующее выражение:
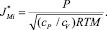 (11)
(11)
Сравнение этого выражения с удельным потоком частиц, полученным в рамках статистической физики [5, с. 110]
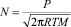 , (12)
, (12)
приводит к выводу о полной их идентичности с точностью до постоянного множителя порядка 2π, что подтверждает правильность выбора характерного линейного размера.
Перейдем непосредственно к описанию процесса переноса вещества из одной фазы в другую. В литературе по массообмену [1–3] принято считать, что при массоотдаче к турбулентному потоку или от него сопротивление переносу массы в значительной степени сосредоточено в тонком слое, прилегающем к границе раздела фаз. Примем эту гипотезу в качестве рабочей. Будем также считать, что для описания неравновесных процессов в приграничном слое можно применить линейное приближение. Тогда результирующая неравновесная плотность потока массы в линейном приближении для изотермических и изобарических условий составит
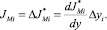 (13)
(13)
Линейное приближение предполагает, что перепад концентраций Δyi мал. Оценим величину этого перепада. Для этого в некотором приграничном объеме, охватывающем как газовую, так и жидкую фазы, выделим ламинарный газовый слой толщиной δy (рисунок). Пусть в этом слое имеет место перепад концентраций 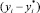 , (где
, (где 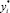 – равновесная концентрация на границе раздела фаз). С позиций НВТ нельзя считать, что концентрация i-го компонента изменяется непрерывно. В силу квантовых эффектов профиль концентраций размытый. Величину этой размытости проще всего оценить, предполагая линейный профиль концентраций в пределах малой толщины слоя δy
– равновесная концентрация на границе раздела фаз). С позиций НВТ нельзя считать, что концентрация i-го компонента изменяется непрерывно. В силу квантовых эффектов профиль концентраций размытый. Величину этой размытости проще всего оценить, предполагая линейный профиль концентраций в пределах малой толщины слоя δy
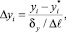 (14)
(14)
где 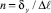 – число элементарных ступенек, каждой из которых соответствует перепад Δyi.
– число элементарных ступенек, каждой из которых соответствует перепад Δyi.
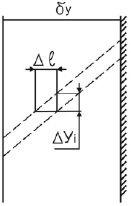
Условия на межфазной границе
Подставляя выражение равновесного мольного потока (10) в (13) и учитывая (14), получим уравнение для неравновесного мольного потока
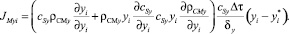 (15)
(15)
Представим мольный поток в виде произведения плотности потока 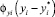 на некоторую скорость переноса сСy, которую будем называть скоростью переноса субстанции
на некоторую скорость переноса сСy, которую будем называть скоростью переноса субстанции
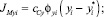 (16)
(16)
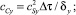 (17)
(17)
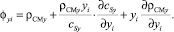 (18)
(18)
Вместо скорости переноса субстанции cCн удобно ввести безразмерную характеристику процесса переноса массы – коэффициент переноса vy, который определяется выражением
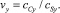 (19)
(19)
Тогда величина неравновесного мольного потока со стороны газовой фазы окончательно запишется следующим образом:
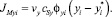 (20)
(20)
На границе раздела фаз допускается существование термодинамического равновесия. Это условие определяется выражением
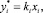 (21)
(21)
где ki – константа фазового равновесия для i-го компонента.
Учитывая условие фазового равновесия (21) и записав выражение для удельного мольного потока в газовой фазе (20) и аналогичное ему выражение для жидкой фазы, получим уравнение для удельного мольного потока через границу раздела фаз
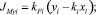 (22)
(22)
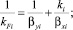 (23)
(23)
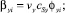 (24)
(24)
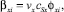 (25)
(25)
где kFi – коэффициент массопередачи i-го компонента; βyi, βxi – коэффициенты массоотдачи i-го компонента соответственно в газовой и жидкой фазах. Величина φyi(φxi), входящая в уравнение для коэффициента массоотдачи, может быть рассчитана теоретически (см. уравнение (18)). Она зависит от физических свойств смеси газа или жидкости (скорости звука, плотности, молярной массы). Безразмерный коэффициент переноса субстанции vy(vx) характеризует гидродинамические условия, в которых протекает процесс массопередачи и теоретически в рамках поставленной задачи определен быть не может. В общем случае коэффициент переноса vy меньше единицы. В пределе он может стать равным единице, и тогда cCy = cSy, δy = Δℓ, то есть процесс переноса массы будет происходить с максимально возможной скоростью, равной скорости звука в данной среде, а толщина пограничного ламинарного слоя δy будет равна характерному линейному размеру Δℓ.
При использовании уравнения массопередачи (22) для расчета массообменного процесса коэффициентами переноса vy и vx необходимо задаваться и корректировать их в зависимости от того, какое распределение концентраций по высоте аппарата необходимо получить.
Таким образом, в рамках нелокальной версии термодинамики удалось раскрыть смысл коэффициентов массоотдачи, выделить в них физическую и гидродинамическую составляющие. Это позволит в дальнейшем по предложенной модели сформировать методику расчета массообменного аппарата, в котором протекает процесс однокомпонентной или многокомпонентной абсорбции. Как видно из предложенной модели, для каждого компонента будет своя плотность потока в газовой 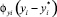 или жидкой
или жидкой 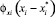 фазе и один для всех компонентов коэффициент переноса vy или vx, который отвечает за гидродинамическую обстановку, существующую в данных условиях массопереноса. Алгоритм расчета по предложенной модели и результаты расчета однокомпонентной и многокомпонентной изотермической абсорбции будут изложены в следующем сообщении.
фазе и один для всех компонентов коэффициент переноса vy или vx, который отвечает за гидродинамическую обстановку, существующую в данных условиях массопереноса. Алгоритм расчета по предложенной модели и результаты расчета однокомпонентной и многокомпонентной изотермической абсорбции будут изложены в следующем сообщении.
Рецензенты:
Фокин В.М., д.т.н., профессор, заведующий кафедрой «Энергоснабжение и теплотехника», ФГБОУ ВПО «Волгоградский государственный архитектурно-строительный университет», г. Волгоград;
Семенов Б.А., д.т.н., профессор, заведующий кафедрой «Промышленная теплотехника», ФГБОУ ВПО «Саратовский государственный технический университет им. Ю.А. Гагарина», г. Саратов.
Работа поступила в редакцию 10.09.2013.



