Эксплуатационные характеристики изделий в значительной мере определяются технологическим процессом их изготовления.
При рассмотрении узла трения «манжетное уплотнение – шейка вала» в силу значительного различия механических свойств (твердости, модуля упругости) трущихся материалов решающую роль на трение и износ резин оказывает шероховатость металлической поверхности вала [1, 2].
Согласно изложенным представлением о природе трения коэффициент трения:
f = F/N = (Fмол + Fдеф)/N = fмол + fдеф, (1)
где F – суммарная сила трения; N – нагрузка, создаваемая силой прижатия кромки манжеты к валу; Fмол и fмол – молекулярно составляющая соответственно силы трения и коэффициент трения; деформационные составляющие.
Адгезионная составляющая коэффициента трения зависит от сил адгезионного взаимодействия и коэффициента упрочнения образовавшейся связи под нагрузкой:
fмол = t0/Pr + b, (2)
где t0 – прочность фрикционной связи, возникающей на фактической площади контакта, при сдвиге; b – коэффициент упрочнения адгезионной связи; Pr – давление на пятне фактического контакта.
Деформационная составляющая коэффициента трения fдеф зависит от отношения глубины внедрения h микронеровности при скольжении к радиусу скругления ее вершины R:
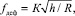 (3)
(3)
где К – коэффициент.
Таким образом, очень гладкие поверхности (параметр шероховатости Rа = 0,04…0,16 мкм) при контакте с манжетой в процессе работы за счет увеличения фактической площади контакта (следовательно, увеличивается t0) имеют большую молекулярную составляющую силы трения. Кроме того, такие поверхности не способны в процессе работы удержать и транспортировать смазку малой вязкости в зону контакта уплотняющего элемента, в результате чего возникает большое сопротивление сдвигу при так называемом пленочном голодании.
Шероховатые, грубые поверхности вала (параметр шероховатости Ra = 2,5...1,25 мкм) удерживают смазку, но под действием нормальных и сдвиговых усилий возникают значительные деформации поверхностного слоя более мягкого материала пары. Коэффициент трения увеличивается вследствие увеличения его деформационной составляющей (т.к. увеличивается отношение h/R). Возможен разрыв смазочной пленки. В результате возникает повышенный износ уплотнения. Шероховатость вала приводит к тому, что контактная поверхность манжеты изнашивается и также становится шероховатой. Это способствует шаржированию манжеты частицами износа и абразива. Таким образом повышенная шероховатость вала оказывает на износ манжеты «двойное» влияние, выражающееся в проявлении упомянутых явлений. Максимальная долговечность манжетного уплотнения достигается при параметре шероховатости Rа = 0,16...0,63 мкм [3]. В работе [3] указывается, что шероховатость вала под герметизатором должна иметь значение Ra ≤ 0,32.
Если рассмотреть пару трения «манжета-вал», то можно отметить, что износ вала также связан с тем, что в месте установки манжеты собираются продукты износа, образовавшиеся в процессе работы зубчатых передач и подшипников в редукторах, коробках передач и шпиндельных головок. Этому способствует вертикальное расположение валов (шпинделей). С другой стороны в уплотнения собираются частицы внешней среды (грязь, абразивные частицы, стружка и т.п.). Попадая в зону контакта манжеты с валом, эти частицы застревают в резине и изнашивают вал.
Вместе с этим обеспечение высокой износостойкости вала в условиях абразивного изнашивания требует повышения твердости его поверхности.
Из всего вышесказанного можно сделать вывод, что наилучшие эксплуатационные характеристики уплотнений достигаются в том случае, когда поверхность трения является гладкой, но в то же время имеет масляные карманы для удержания смазки в сопряжении. Проявлению гидродинамического эффекта в сопряжении способствует нанесение на гладкую поверхность вала микрорельефа определенного вида.
Процесс алмазного выглаживания кинематически аналогичен точению [5], только вместо резца применяется алмазный выглаживатель, который, пластически деформируя поверхностный слой, выравнивает и упрочняет его.
По сравнению с традиционными методами финишной обработки (тонкое шлифование, хонингование, суперфиниширование, полирование) метод выглаживания имеет ряд преимуществ [3]:
– обеспечивается более эффективное снижение шероховатости заготовки, что позволяет в ряде случаев сокращать количество переходов и операций;
– обработанная поверхность характеризуется округлым профилем и относительно большой опорной поверхностью;
– поверхностный слой изделий упрочняется, формируется мелкозернистая структура, образуются благоприятные остаточные напряжения сжатия.
Указанные преимущества проявляются в улучшении эксплуатационных характеристик изделий: повышении долговечности, износостойкости и усталостной прочности.
При обработке поверхностей, работающих в условиях трения, долгое время основным параметром, описывающим требования к микрогеометрии поверхности детали, являлся параметр шероховатости Ra, мкм. Однако, как показывает тенденция развития машиностроения, в настоящее время одного параметра недостаточно, и все чаще к поверхностям деталей машин, работающих в условиях трения, предъявляют требование в виде наличия регулярного микрорельефа.
В работе [5] предложен метод алмазного выглаживания с наложением продольных колебаний (рис. 1), в результате которых на поверхности детали формируется микрорельеф.
Согласно экспериментальным и теоретическим исследованиям, приведенным в работах [1, 5], можно классифицировать получаемые микрорельефы при вибровыглаживании на несколько видов (рис. 2). При этом на практике характер микрорельефа зависит от параметров обработки и прежде всего от следующих параметров: S – подача выглаживающего индентора, мм/об; R – радиус индентора, мм; h – глубина внедрения индентора, мм; А – амплитуда колебания инструмента, мм; ω – частота колебаний инструмента, Гц.
Для обеспечения прогнозирования получаемого микрорельефа поверхностей деталей в зависимости от указанных параметров обработки была необходима разработка математической модели.
При построении математической модели процесса обработки ППД, позволяющей моделировать рельеф обработанной поверхности в зависимости от параметров и условий обработки, необходимо рассмотреть процесс формообразования поверхности, в котором образующей будет кривая, описывающая профиль рабочей поверхности инструмента, а направляющей ‒ траектория движения вершины инструмента по обрабатываемой поверхности.
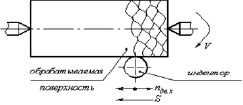
Рис. 1. Схема нанесения микрорельефа алмазным выглаживанием
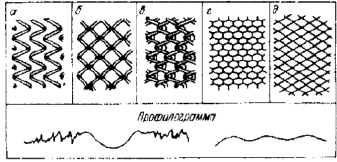
Рис. 2. Схемы и профилограммы поверхностей с системами канавок (а, б, в) и полностью новым регулярным микрорельефом (г, д), регламентированные ГОСТ 24773-81 поверхности с регулярным микрроельефом
Для того чтобы произвести процесс моделирования обработки, предлагается следующий подход к решению данной задачи [4]:
– обрабатываемую цилиндрическую поверхность, например шейку вала, разбить на Kx точек вдоль оси x и на Kу точек по окружности детали (рис. 3, а);
– далее для упрощения расчета произвести развертку цилиндрической поверхности (рис. 3, б).
Для того чтобы получить геометрию поверхности, необходимо рассчитать координаты каждой точки модели, представленной на рис. 3, б.
а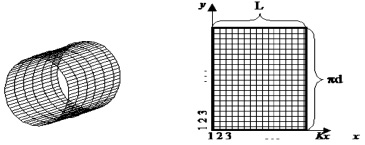 б
б
Рис. 3. Интерполяция обрабатываемой поверхности: а – модель обрабатываемой поверхности; б – разработка модели обрабатываемой поверхности
Для более наглядной интерпретации результатов расчета целесообразнее представить результат в виде матрицы размером Кх×Ку, где каждый элемент матрицы будет численно выражать высоты микронеровностей поверхности по оси Z.
При разбиении цилиндрической развертки на точки (Кх×Ку) следует учесть, что необходимо учесть возможность расчета геометрии после нескольких оборотов, тогда исходя из рис. 3, б, точки (1, 1...Кх) совпадут с точками (Ку, 1...Кх), поэтому разбиение целесообразнее производить так, как показано на примере, представленном на рис. 4.
На рис. 4 показан пример графической интерпретации матрицы размером 4×4. Очевидно, что для представления микропрофиля поверхности разбиение на такое количество точек неэффективно, значения Кх и Ку должны как минимум быть на порядок выше, но следует также учесть, что увеличение количества рассчитываемых точек приводит к более громоздким расчетам.
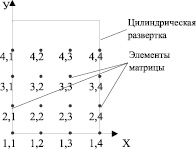
Рис. 4. Пример представления цилиндрической развертки в виде матрицы
Детальность расчета микропрофиля можно оценить величинами:
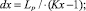 (4)
(4)
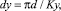 (5)
(5)
где Lр – ширина обрабатываемого участка, мм; Kx – количество точек рассчитываемых по оси х; Kу – количество точек рассчитываемых по оси у; d – диаметр обрабатываемой детали; dx, dy – интервал между рассчитываемыми точками по оси х, у соответственно, мм.
При этом уравнение, описывающее рабочую поверхность выглаживающего инструмента в математической модели примет вид:
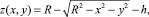 (6)
(6)
где R – радиус индентора, мм; h – глубина внедрения индентора, мм.
При этом положение инструмента по оси Х можно определить по формуле:
 (7)
(7)
где S – подача выглаживающего индентора, мм/об; N – число совершенных оборотов детали, за время обработки.
Для обеспечения регулярного микрорельефа на поверхности детали [5] при усложнении кинематики движения инструмента (придания в процессе выглаживания индентору возвратно-поступательных колебаний вдоль оси обрабатываемой детали), в математическую модель необходимо внести изменения, обеспечивающие изменение траектории движения индентора, описываемое уравнением:
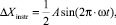 (8)
(8)
где ΔXinstr – корректировка положения инструмента в процессе обработки с учетом совершения колебательных движений, мм; А – амплитуда колебания инструмента, мм; ω – частота колебаний инструмента, Гц.
С использованием выражений (4–8) была построена математическая модель, реализованная в среде математического программирования MatLab 12R, позволяющая моделировать микрорельеф обработанной поверхности.
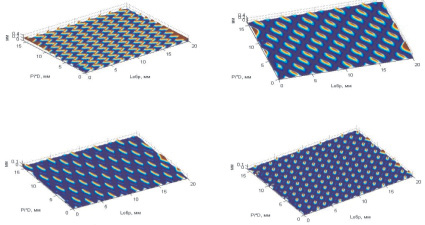
Как показали результаты моделирования (рис. 5), результаты адекватны и полностью коррелируют с теоретическими данными, представленными на рис. 2.
в г
Рис. 5. Результаты моделирования поверхностей с системами канавок (а, б, в) и полностью новым регулярным микрорельефом (г), регламентированные ГОСТ 24773-81 поверхности с регулярным микрорельефом
При проведении дальнейших исследований, предполагается внести в математическую модель ряд алгоритмов, учитывающих микрорельеф исходной поверхности обрабатываемой детали, получаемой на предыдущих операциях и алгоритмов, учитывающих упруго-пластические свойства обрабатываемой поверхности.
Проведение НИР осуществляется в рамках реализации ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009–2013 годы и при поддержке гранта Президента Российской Федерации МК-6076.2013.8.
Рецензенты:
Васильев А.В., д.т.н., профессор, директор Института химии и инженерной экологии Тольяттинского государственного университета, г. Тольятти;
Горшков Б.М., д.т.н., доцент, заведующий кафедрой «Электротехнические комплексы и системы», ГОУ ВПО «Поволжский государственный университет сервиса», г. Тольятти.
Работа поступила в редакцию 20.09.2013.



