Эффективность дистанционного образования может быть существенно повышена путем построения индивидуальной трассы изучения учебного материала, основанной на знаниях об обучаемом, приобретенных во время его работы с системой дистанционного обучения (СДО). В современных СДО индивидуальную трассу обучения формирует преподаватель, который в большинстве случаев ориентируется на усредненного по своей подготовленности ученика и не учитывает реальных знаний конкретного обучаемого. При этом не учитывается психологический тип личности обучаемого, который согласно исследованиям, проведенным в работах [5, 6], непосредственно влияет на эффективность процесса обучения. В данной работе не ставится цель исследовать множество существующих психологических типов личностей. Однако в качестве одной из важных задач считается получение математического формализма, дающего возможность учитывать такие типы, каким бы сложным разнообразием они ни отличались. Автоматизация формирования индивидуальной трассы обучения, учитывающей психологический тип личности, а также реальные знания обучаемого на конкретный момент времени, позволит повысить эффективность работы СДО.
Целью работы является разработка математического формализма, достаточного для адекватной классификации обучающихся по широкому спектру психологических свойств их личностей, с целью выявления наиболее эффективных учебных ресурсов, пригодных обучаемым с конкретными психологическими особенностями и текущим уровнем знаний.
Методы исследования. Методы общей алгебры и теории множеств.
Результаты исследования и их обсуждение
При выборе учебного материала для усвоения навыков решения какого-либо класса задач помимо психологического типа личности обучаемого необходимо учитывать соответствующие особенности учебного материала и особенности тестовых задач [3]. Перед тем как начать обучение, необходимо обеспечить все основные элементы ситуации, при которых обучение будет наиболее эффективным, а именно:
– обучающемуся должен быть предоставлен учебно-методический материал, достаточный по своему содержанию для достижения поставленных целей обучения;
– учебно-методический материал должен соответствовать уровню подготовленности обучающегося;
– материал должен соответствовать по форме изложения, сложности и подробности психологическому типу личности обучающегося;
– тестовая задача на конкретный момент времени должна соответствовать уровню подготовленности обучаемого с учетом психологического типа личности;
– последовательность предлагаемого материала и тестовых заданий должна соответствовать психологическому типу обучающегося.
Для достижения сформулированных условий необходимо рассматривать следующие основные понятия:
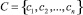– множество понятий предметной области,
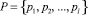– множество тестовых задач,
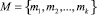– множество единиц учебно-методического материала (элементы учебного материала),
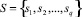– множество обучаемых,
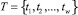– множество психологических типов личности.
Сложность тестовой задачи pi может быть выражена через функцию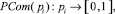 
отображающую множество существующих задач в отрезок действительных чисел:
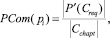
где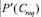 
– мощность множества требуемых понятий тестовой задачи; 
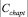– мощность множества всех понятий курса.
Аналогичным образом может быть определена сложность единицы учебного материала mi, функция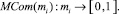 
отображает множество существующих учебно-методических материалов в отрезок действительных чисел:
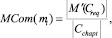
где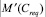 
– мощность множества понятий, требуемых для изучения единицы учебно-методического материала.
Дифференциация типов определяется тем, насколько просто изучается заданный учебный материал, или насколько легко решается предложенная задача различными по психологическим типам обучающимися. Так, например, каждому элементу из множества единиц учебного материала можно сопоставить подмножество психологических типов, которые наиболее просто смогут усвоить этот материал. Это задается с помощью функционального соответствия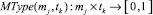 
:
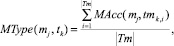
где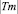 
– мощность множества характеристик единицы учебно-методического материала, используемых при определении психологического типа личности обучаемого; 
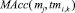– функция определения соответствия единицы материала mj i-й характеристике k-го типа личности tmk,i.
Аналогично, для определения типа задачи можно также использовать аналогичное соответствие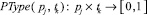 
:
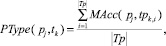
где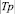 
– мощность множества характеристик тестовой задачи, используемых при определении психологического типа личности обучаемого; 
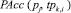– функция определения соответствия задачи pj i-й характеристике k-го типа личности tpk,i .
Рассмотрим выражения, формализующие степень усвоения понятий предметной области обучающимся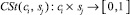 
и степень его принадлежности определенному типу личности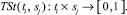 
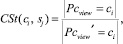
где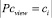 
– мощность множества задач, решенных j-м обучаемым, в которых текущее понятие считается рассмотренным; 
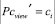– мощность множества задач как решенных j-м обучаемым, так и не решенных, в которых текущее понятие считается рассмотренным.
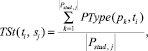
где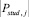 
– мощность множества всех решенных пользователем задач.
Зададим два соответствия, основанных на семантике понятий предметной области обучения:
– соответствие понятия ci учебному материалу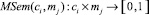 
:
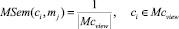
где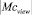 
– мощность множества рассмотренных понятий единицы учебно-методического материала;
– соответствие понятия ci выбираемой тестовой задаче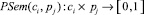 
:
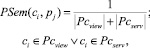
где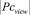 
– мощность множества рассмотренных понятий тестовой задачи; 
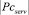– мощность множества вспомогательных понятий тестовой задачи.
Целью выбора материала, как подмножества 
и тестовых задач, как подмножества 
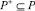, является такой подбор учебно-методического материала и тестовых задач, который был бы достаточен для освоения навыков обучающимся с известным психологическим типом личности и уровнем первоначальных знаний:
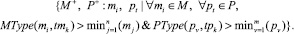
Главным принципом выбора материала, как подмножества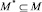 
и тестовых задач, как подмножества 
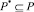, является такое формирование последовательности предоставления учебно-методического материала и тестовых задач, которое соответствовало бы психологическому типу обучающегося, его текущей подготовленности с учетом уровней сложности задач, при которых обеспечивался бы минимальный срок усвоения материала:
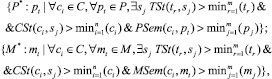
где функция вычисляет допустимые границы из отрезка отнесения элементов выделенным множествам. Здесь использованы четыре разных функции min, вычисляющие границы для tr, ci, pj, mj. Однако для упрощения восприятия формул они были объединены в одну функцию.
Далее, принимая во внимание полную формулировку принципа отбора итоговых множеств материала M0 и задач P0, необходимо вычислить пересечение полученных множеств:
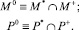
Полученные множества содержат материал и задачи, выбранные специально для обучающегося определенного психологического типа, а также для предметной области, понятия которой должен усвоить этот обучающийся.
Заключительным этапом формирования выборки задач и материала должен стать этап упорядочения элементов множеств M0, P0 для формирования индивидуальной трассы обучения. Результат этого этапа достигается упорядочением множеств с помощью функций сложности:
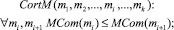
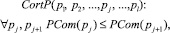
где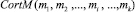 
и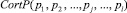 
соответственно кортежи последовательности выбора материалов и последовательности предложения тестовых задач.
Выводы
В статье предложен математический формализм, позволяющий классифицировать обучающихся по набору их психологических характеристик и уровню знаний на конкретный момент времени. Результатом такой классификации является формирование индивидуальной последовательности изучения единиц учебно-методического материала и решения тестовых задач, соответствующей психологическому типу личности и уровню подготовленности обучаемого. Применение предложенного подхода в рамках системы дистанционного обучения позволит повысить эффективность образовательного процесса за счет адаптации процесса обучения под нужды конкретного обучаемого.
Рецензенты:
Пылькин А.Н., д.т.н., профессор, заведующий кафедрой ВПМ, ФГБОУ ВПО «Рязанский государственный радиотехнический университет», г. Рязань;
Каширин И.Ю., д.т.н., профессор кафедры ВПМ, ФГБОУ ВПО «Рязанский государственный радиотехнический университет», г. Рязань.
Работа поступила в редакцию 10.09.2013.