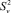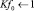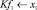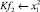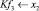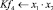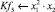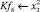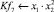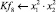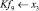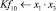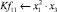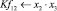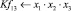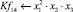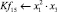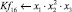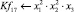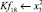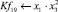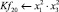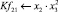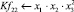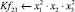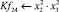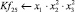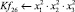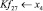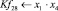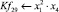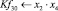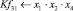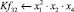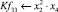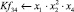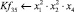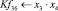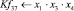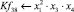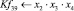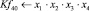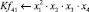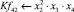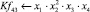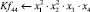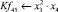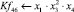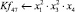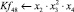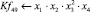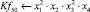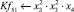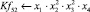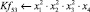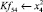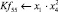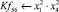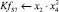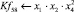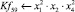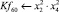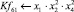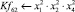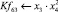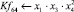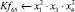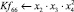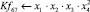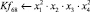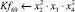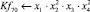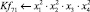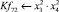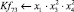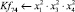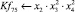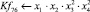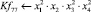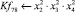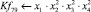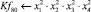Современный уровень развития ледокольной техники позволяет организовать транспортировку лесоматериалов по рекам и водохранилищам в продленный период навигации. Продление навигации может быть обеспечено прокладкой каналов в ледовом поле в ранне-весенний и осенний периоды навигации [2; 4].
В связи с этим возникает необходимость аналитического и экспериментального исследования закономерностей движения плота в ледовом канале.
Цель исследования – получить математические модели полного ледового сопротивления, сопротивления воды, чистого ледового сопротивления движению плота в зависимости от длины плота, толщины льда, скорости буксировки, отношения ширины канала к ширине плота.
Для получения опытных данных был проведен полнофакторный трехуровневый эксперимент по определению чистого ледового сопротивления движению плота. В силу ограниченности условий проведения опытов была взята модель сегмента плота масштабом 1:15 с линейными размерами L×B×T (2,4×0,6×0,1 м), где L – длина сегмента плота, B – ширина сегмента плота, T – осадка сегмента плота. Гидродинамические условия смоделированы с учетом критерия подобия Фруда [1]. Опыты проводились с натурным льдом в полевых условиях на озере острова Татышева (56°01′43′′N 92°56′47′′E). В качестве входных регулируемых параметров были приняты (табл. 1):
● Длина сегмента плота (Lпл) –
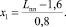
● Толщина битого льда в канале (hл) –
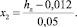
● Скорость буксировки сегмента плота в ледовом поле (υпл) –
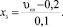
● Отношение ширины канала к ширине сегмента плота (Kв) –
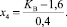
Таблица 1
Входные регулируемые параметры эксперимента по определению сопротивления битого льда движению плота
|
Уровень |
Значения факторов |
||||
|
Xi |
Lпл, м |
hл, м |
υпл, м/с |
Kв |
|
|
1 |
–1 |
0,8 |
0,007 |
0,1 |
1,2 |
|
2 |
0 |
1,6 |
0,012 |
0,2 |
1,6 |
|
3 |
+1 |
2,4 |
0,017 |
0,3 |
2 |
Функциями отклика связывающие входные параметры, характеризующие результаты эксперимента, с варьируемыми переменными, являются:
– Полное ледовое сопротивление (δп), Н.
– Сопротивление воды (δв), Н.
– Чистое ледовое сопротивление (δчл), Н; δчл = δп – δв.
При числе параллельных опытов m = 5 и числе уровней каждого фактора, равного трем, получено 405 опытных значений в каждой функции отклика.
Обработка экспериментальных данных проведена в математическом пакете Mathcad.
Дисперсия воспроизводимости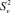 
и ошибки опытов (воспроизводимости) Sv, расчетные значения критерия Кохрена Gp для полного ледового сопротивления δп, сопротивления воды δв и чистого ледового сопротивления δчл представлены в табл. 2.
Таблица 2
Значения дисперсий воспроизводимости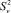 
, ошибок опытов Sv и расчетных значений критерия Кохрена Gp для δп, δв, δчл
|
δп |
δв |
δчл |
|
|
|
0,0005 |
0,0003 |
0,0008 |
|
Sv, Н |
0,0233 |
0,016 |
0,028 |
|
Gp |
0,038 |
0,034 |
0,039 |
Гипотеза однородности дисперсий не отклоняется при уровне значимости α = 0,05 (Gp < Gтаб = 0,059, где Gтаб – критическое значение критерия Кохрена).
Математическая модель полнофакторного эксперимента, описывающая зависимость ледового сопротивления от рассматриваемых входных величин, содержит 81 коэффициент регрессии. Матрица функций от входных параметров при коэффициентах модели имеет вид:
|
|
|
|
|
Для оптимизации и сжатия математической модели (уменьшения размерности ее коэффициентов) принято условие 5 %-й ошибки от среднего значения выходных значений, что допустимо при проведении технологических расчетов лесосплавных работ.
По составленной программе в системе MathCаd для каждой из моделей вычислены их коэффициенты матричным методом наименьших квадратов, расчетные значений δ, стандартные ошибки коэффициентов, расчетные значения критерия Стьюдента оценки значимости отличия коэффициентов от нуля, дисперсии адекватности, стандартные ошибки и коэффициенты детерминации моделей, проведена оценка адекватности модели по критерию Фишера и выполнена процедура сжатия модели [3, 5].
После выполнения процедуры сжатия в математических моделях δп, δв, δчл осталось соответственно 12; 7 и 15 коэффициентов регрессии:
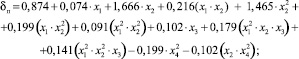
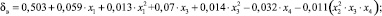
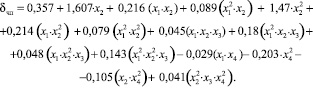
Результаты сопоставления расчетных и фактических значений δп, δв, δчл представлены на рис. 1–3.
Стандартные ошибки (S), коэффициенты детерминации (R2) и число степеней свободы (f) полученных моделей представлены в табл. 3.
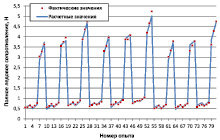
Рис. 1. Расчетные и фактические значения ледового сопротивления движению сегмента плота
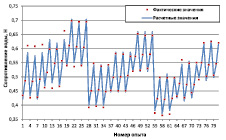
Рис. 2. Расчетные и фактические значения сопротивления воды движению сегмента плота
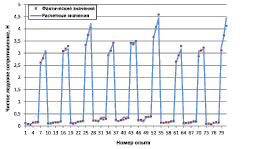
Рис. 3. Расчетные и фактические значения чистого ледового сопротивления движению сегмента плота
Таблица 3
Характеристики точности моделей δп, δв, δчл
|
δп |
δв |
δчл |
|
|
S |
0,084 |
0,012 |
0,061 |
|
R2 |
0,997 |
0,99995 |
0,999 |
|
f |
69 |
74 |
66 |
Выводы
Получены адекватные эксперименту модели полного ледового сопротивления, сопротивления воды, чистого ледового сопротивления движению плота, учитывающие скорость буксировки, длину плота, толщину льда в канале, отношение ширины канала к ширине плота. Полученные результаты необходимы для определения оптимальных условий организации лесосплавных работ в период продленной навигации и соответствующих технико-экономических показателей.
Рецензенты:
Полетайкин В.Ф., д.т.н., профессор, заведующий кафедрой технологии и машин природообустройства, ФГБОУ ВПО «Сибирский государственный технологический университет», г. Красноярск;
Лозовой В.А., д.т.н., профессор, заведующий кафедрой технологии и оборудования лесозаготовок, ФГБОУ ВПО «Сибирский государственный технологический университет», г. Красноярск.
Работа поступила в редакцию 18.09.2013.