Программируемые логические интегральные схемы (ПЛИС) получили широкое распространение в современных цифровых устройствах, используемых в цифровой обработке сигналов, передаче данных, системах хранения, а также для проектирования и прототипирования интегральных схем специального назначения. Особенностью ПЛИС является то, что логика их работы задается путем программирования, то есть может быть оперативно изменена прямо во время использования устройства. Такая особенность приводит к возможности гибкой настройки схемы для конкретной решаемой задачи за короткий срок.
Отдельно стоит отметить активное применение ПЛИС в аппаратуре специального назначения, которая используется в области космонавтики и управления ответственными промышленными объектами [2]. Для таких областей особую важность имеет надежность устройства, то есть устойчивость к различным сбоям. Одним из подходов к повышению отказоустойчивости ПЛИС является использование в качестве элементной базы функционально-полных толерантных элементов (ФПТЭ) [3]. Их основным свойством является сохранение функциональной полноты при однократных константных отказах, что позволяет по-прежнему использовать их в схеме, даже если такой отказ произошел.
Способность ПЛИС к реконфигурации также может быть использована для повышения отказоустойчивости. В случае отказа логического элемента, расположение логических блоков на схеме может быть изменено таким образом, чтобы вместо отказавшего элемента был задействован резервный. Для такой реконфигурации нужно в первую очередь определить место и вид отказа, то есть решить задачу диагностики.
Постановка задачи диагностирования ПЛИС на базе ФПТЭ
Задача диагностирования заключается в поиске диагностического теста. Разработку тестов будем вести для модели однократных константных отказов функционально-полных толерантных элементов. Каждый ФПТЭ может находиться в одном из 9 состояний [3], включая полностью работоспособное состояние и 8 состояний частичных отказов (по 2 вида отказа на каждый из четырех входов), при которых элемент сохраняет функциональную полноту и может быть частично использован после реконфигурации. Если всего в схеме устройства задействовано N ФПТЭ и одновременно может произойти не более k отказов, то общее количество получаемых неисправных модификаций равно
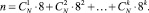
В приведенной формуле первое слагаемое соответствует возникновению одного отказа, второе слагаемое – двух отказов, и так далее. Пусть дано исправное цифровое устройство A0. Из него, используя заданный класс неисправностей, порождается множество всех неисправных модификаций A = {A1, A2, ..., An}, где A0 ≠ Ai, i = 1...n. Пусть x = (x(1), x(2), …, x(t)) – последовательность входных сигналов. Если подать эту последовательность на вход устройства Ai, на выходе мы получим последовательность выходных сигналов yi = Ai(x) = (yi(1), yi(2), …, yi(t)). Диагностическим тестом для заданного устройства называется такая последовательность входных сигналов x, что для любой пары устройств Ai и Aj, i ≠ j соответствующие последовательности выходных сигналов yi и yj будут различны. Иными словами, по выходной последовательности y можно однозначно определить номер тестируемого устройства i, y = Ai(x), а, следовательно, и саму неисправность.
В соответствии с ГОСТ 27.002-89, одним из комплексных показателей надежности является коэффициент готовности, который представляет собой отношение времени исправной работы к сумме времен исправной работы и вынужденных простоев объекта. При возникновении отказа в ПЛИС время простоя будет определяться временем диагностирования и временем реконфигурации схемы. Таким образом, сократив время диагностирования ПЛИС, можно повысить коэффициент готовности устройства. Время диагностирования, в свою очередь, определяется длиной диагностического теста t.
Резюмируя вышесказанное, можно сформулировать задачу диагностирования ПЛИС следующим образом. Дано: схема устройства на языке описания аппаратных устройств (например, VHDL). Получить: диагностическую последовательность минимальной длины. Таким образом, задача диагностирования может рассматриваться как задача оптимизации. Существуют различные методы построения диагностических последовательностей. Однако современные ПЛИС содержат миллионы транзисторов, и количество различных входных последовательностей для них очень велико. В связи с этим применение точных алгоритмов оказывается невозможно, и на практике применяют различные эвристические подходы.
Для рассмотрения возможности применения генетических алгоритмов (ГА) для решения поставленной задачи и построения наиболее эффективного алгоритма необходимо изучить накопленный опыт применения ГА для решения других задач оптимизации.
Генетические алгоритмы
Генетический алгоритм представляет собой адаптивный поисковый метод, основанный на селекции лучших элементов в популяции. Цель генетических алгоритмов состоит в том, чтобы моделировать естественные эволюционные процессы для эффективного решения оптимизационных задач. Обзор литературы позволяет утверждать, что генетические алгоритмы получили широчайшее применение в задачах науки и техники, успешно используются для решения задач, имеющих важное теоретическое значение и практическую ценность ([11, 9, 4]).
Во многих работах генетические алгоритмы используются как вспомогательный инструмент при построении и обучении нейронных сетей. Причем ГА используются на разных этапах: как для настройки архитектуры нейронной сети, так и на этапе обучения, для настройки весов дуг и других параметров (например, [10]).
Очень широко распространено применение генетических алгоритмов в промышленных задачах, в том числе для разработки интегральных схем и микропроцессорных систем (например, [11]). ГА применяются также в химической промышленности, например, для настройки параметров технологических процессов, а также при проектировании различных технических систем, оптимизации режимов электроэнергетических систем, управления динамическими системами и анализа их поведения, а также на отдельных этапах управления предприятием.
Генетические алгоритмы в задачах криптоанализа
Задача криптоанализа состоит в том, чтобы найти секретный ключ, то есть среди множества всех возможных решений (ключей) необходимо найти оптимальное (ключ, верно расшифровывающий шифртекст). При этом у нас нет четкой математической формулы, которая бы описывала зависимость «оптимальности» ключа от самого ключа. Таким образом, мы имеем дело со слабо формализованной оптимизационной задачей, а именно для такого класса задач генетические алгоритмы зарекомендовали себя с лучшей стороны.
Возможность применения генетических алгоритмов к задачам криптографии рассматривается в работе [6]. Работа имеет во многом реферативный характер. В основном в ней рассмотрены проводимые ранее атаки на исторические схемы шифрования. При этом генетические алгоритмы не оптимизируются под конкретную решаемую задачу, а используются в стандартном виде. Вопросы выбора наиболее оптимального способа кодирования особей, а также выбора удачной функции приспособленности не решаются. Кроме того, не исследуется влияние параметров генетического алгоритма на сходимость и скорость сходимости алгоритмов. Результаты приводимых атак нельзя назвать успешными. Характеристики, показываемые приводимыми алгоритмами, не лучше результатов других известных атак. В книгах [5, 8] рассматривается использование генетических алгоритмов для перестановочных шифров. В этих работах фигурирует несколько интересных идей. Во-первых, стандартная оценка на основе частот заменяется системой подсчета очков. Во-вторых, здесь же высказывается идея, что при помощи генетических алгоритмов можно вычислять не только сам ключ при известной длине, но и длину ключа. По поводу данных работ можно заметить, что криптоанализу подвергался весьма ограниченный набор сообщений. При этом очевидно, что очень сильно учитывались статистические характеристики этих текстов, что ставит под сомнение возможность переноса полученных результатов на другие входные данные. Также к недостаткам можно отнести отсутствие обоснования выбора конкретных операторов генетического алгоритма и фитнесс-функции.
Пример успешного применения ГА в задаче криптоанализа приводится в статье [7]. Авторами разработан и описан генетический алгоритм для поиска секретного ключа блочного перестановочного шифра. Ключом в данном случае является перестановка начального фрагмента натурального ряда. Разработанный алгоритм точно определяет длину секретного ключа и с регулируемой «точностью» находит саму секретную перестановку. Анализ результатов вычислительного эксперимента свидетельствует о возможности почти полного автоматического дешифрования текста.
Генетические алгоритмы в задачах составления расписаний
В наиболее общей формулировке задачи составления расписаний, как правило, состоят в следующем. С помощью некоторого множества ресурсов или обслуживающих устройств должен быть выполнен некоторый фиксированный набор работ (заданий). Цель заключается в том, чтобы при заданных свойствах работ и ресурсов и наложенных на них ограничениях найти эффективный алгоритм упорядочивания работ, оптимизирующий длину расписания (время, за которое будут выполнены все задания) или среднее время пребывания заданий в системе. Задания могут быть либо независимыми, либо формировать граф зависимостей, определяющий отношение частичного порядка на множестве заданий.
Сложность задачи составления расписания заключается в том, что в каждый момент времени мы можем по-разному выбрать задания и назначить их различным процессорам. Таким образом, количество возможных вариантов распределения заданий растет экспоненциально с ростом числа заданий и числа ресурсов, поэтому полный перебор всех вариантов для большого количества заданий на практике неприменим.
Для решения сложных задач составления расписания с большим числом дополнительных условий часто применяются генетические алгоритмы. При этом каждая хромосома кодирует некоторое допустимое расписание. В качестве генов обычно рассматриваются номера эвристик. На сегодняшний день эта идея известна как метод комбинирования эвристик (HCM – Heuristics Combination Method) [1].
Генетические алгоритмы для тестирования цифровых устройств
Существуют различные методы построения тестовых последовательностей. Но для больших цифровых устройств с количеством вентилей в реализации от 5 тысяч, проектирование которых осуществляется в настоящее время, задача построения тестов остаётся открытой. Применение точных методов при таких объёмах входных данных невозможно, поэтому используют различные приближённые алгоритмы.
Для генерации тестов ГА применяются, начиная с середины 90-х годов. В первых работах, где для решения задачи построения тестов использовались ГА, особи представляли собой простые двоичные векторы, а не тестовые последовательности. Функция приспособленности для такой особи рассчитывалась как количество неисправностей, которые мог выявить данный тест. Операции скрещивания и мутации ничем не отличались от канонического ГА. Позднее появились работы, где в качестве особи ГА рассматривалась двоичная матрица, соответствующая входной тестовой последовательности. Такое кодирование на данный момент считается стандартным на логическом уровне представления цифровых устройств.
Необходимость дальнейшего развития идеи применения ГА возникла ввиду наличия общей проблемы данного метода – излишне быстрой сходимости популяций. В результате такой сходимости тестовая последовательность, получаемая ГА, не всегда выявляла все неисправности – часть оставалась не протестированной к моменту завершения работы ГА по лимиту времени. Для решения этой проблемы были разработаны гибридные алгоритмы, в которых на первом этапе работал ГА, а при сходимости популяции происходил переход ко второму этапу, где использовался структурный метод построения тестовой последовательности.
Следующим этапом развития ГА стало появление их параллельных версий. Параллельные реализации ГА в области построения тестов не отличаются принципиально от параллельных реализаций ГА, применяемых для решения других задач – использование мелкоячеистой (параллельное вычисление фитнесс-функции) и крупноячеистой (островная модель) структур. Как правило, для тестирования этих алгоритмов используются слабопараллельные (2-4-х ядерные процессоры) и сильнопараллельные (8 и более ядер) вычислительные системы. Но в последнее время появились данные об использовании технологии CUDA многоядерных графических ускорителей. Хотя в последнем случае возможна лишь мелкоячеистая структура распараллеливания, зато коэффициент ускорения вычислений может быть весьма значительным.
Кроме непосредственного получения тестовых последовательностей, ГА может быть использован для сопутствующих задач, например, для удаления избыточной информации из диагностических словарей.
Заключение
Приведенный выше обзор позволяет утверждать, что генетические алгоритмы получили широчайшее применение в задачах науки и техники, успешно используются для решения задач, имеющих важное теоретическое значение и практическую ценность. При этом очевидно, что качество и эффективность используемых генетических алгоритмов играют главную роль в определении качества и скорости решения конкретной задачи.
Нужно заметить, что решаемые задачи постоянно усложняются, объемы данных, а, следовательно, и объемы вычислений, постоянно растут. Это требует усовершенствования подходов и методов, используемых при решении задач.
Принимая во внимание положительный опыт применения генетических алгоритмов для тестирования цифровых устройств, представляется оправданным построение генетического алгоритма для задачи диагностирования ПЛИС на базе функционально-полных толерантных элементов. При этом приведенный обзор позволяет сделать вывод, что на эффективность ГА существенное влияние оказывает правильный выбор способа кодирования особей, а также правильный выбор параметров. Таким образом, при разработке ГА диагностирования ПЛИС необходимо первоочередное внимание уделить выбору способа кодирования, который бы позволил применять стандартные генетические операторы, а также полноценно исследовать эффективность алгоритма при различных значениях параметров с тем, чтобы выбрать наиболее подходящие для конкретной задачи.
Рецензенты:
Южаков А.А., д.т.н., профессор, заведующий кафедрой «Автоматика и телемеханика», ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь.
Русаков С.В., д.ф.-м.н., профессор, заведующий кафедрой прикладной математики и информатики, ФГБОУ ВПО «Пермский государственный национальный исследовательский университет», г. Пермь.
Работа поступила в редакцию 16.09.2013.



