Рассматривается бесконечная цилиндрическая оболочка толщины h с радиусом срединной поверхности R. Колебания такой оболочки под нагрузкой, плотность которой обозначим p1, p2, pn соответственно, можно описать, следуя [1, 2, 4], уравнениями:
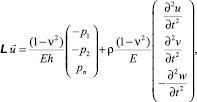 (1)
(1)
где
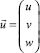 – вектор перемещения с осевой, окружной и радиальной компонентами соответственно (знак «+» перед pn и знак «–» перед последней компонентой инерционного члена говорит о том, что положительным считается перемещение по направлению к центру кривизны); ρ – плотность материала оболочки; E – модуль Юнга; ν – коэффициент Пуассона,
– вектор перемещения с осевой, окружной и радиальной компонентами соответственно (знак «+» перед pn и знак «–» перед последней компонентой инерционного члена говорит о том, что положительным считается перемещение по направлению к центру кривизны); ρ – плотность материала оболочки; E – модуль Юнга; ν – коэффициент Пуассона, 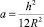 .
.
При рассмотрении задачи по моментной теории оболочек матрица оператора L имеет вид
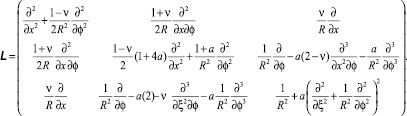 (2)
(2)
Перейдём к безразмерной осевой координате 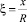 и домножим на R2 систему (1).
и домножим на R2 систему (1).
Матрица полученной системы примет вид
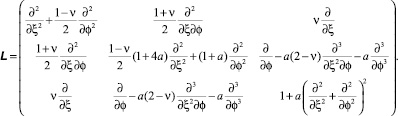 (3)
(3)
Будем искать решения преобразованной таким образом системы (1) в виде
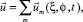 (4)
(4)
где 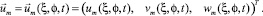
Компоненты 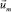 примем в виде
примем в виде
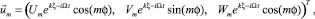 (5)
(5)
где Ω – частота; k = λR – приведенное осевое волновое число; λ – осевое волновое число; m – окружное волновое число (число окружных волн), принимающее значения m = 1, 2, 3… Случай m = 0 (осесимметричные колебания) является предметом отдельного исследования и здесь не рассматривается.
Такой подход позволит искать решение задачи для каждого фиксированного значения окружного волнового числа m независимо.
Предположим, что оболочка заполнена жидкостью, движение которой описывается (см. [1]) уравнением для потенциала скоростей
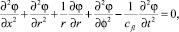 (6)
(6)
где cfl – скорость звука в жидкости.
Выберем модель несжимаемой жидкости, в этом случае будем считать cfl → ∞.
Условия «непротекания» на границе жидкость-оболочка имеют вид
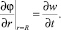 (7)
(7)
Наличие жидкости учтем в составе pn уравнения (1а), а p1 и p2 считаем равными нулю.
Решение уравнения (6) будем искать в виде
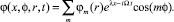 (8)
(8)
Это позволит также искать решение независимо для каждого значения m. Подстановка (8) в (6) с учётом cfl → ∞ приводит к уравнению Бесселя
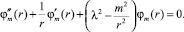 (9)
(9)
Его решение имеет вид
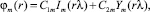 (10)
(10)
где C1m и C2m – некоторые константы; Im(rλ) и Ym(rλ) – модифицированные функции Бесселя (см. [3]).
Из-за ограниченности потенциала скоростей при r → 0 имеем C2m = 0, тогда подстановка (8) в (7) с учетом (5) позволяет найти C1m, затем ϕm(R) и получить окончательно давление жидкости на стенку оболочки в виде
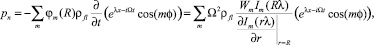 (11)
(11)
где ρfl – плотность жидкости.
Таким образом, в правую часть последнего уравнения системы войдет
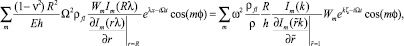 (12)
(12)
где 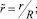
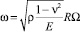 – приведённая частота.
– приведённая частота.
Перенесем правые части преобразованной системы (1) налево, подставим в полученные соотношения формулы (4) с учетом (5) и (12), уберем символ 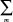 и разделим все уравнения на
и разделим все уравнения на 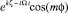 . Тогда получим матричное уравнение
. Тогда получим матричное уравнение
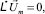 (13)
(13)
где 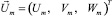 , с матрицей оператора L* в виде
, с матрицей оператора L* в виде
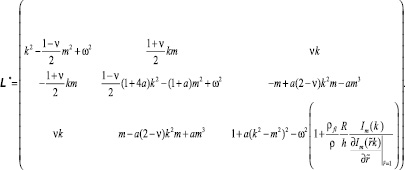 (14)
(14)
В отсутствие жидкости (пустая оболочка) в 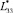 надо принять ρfl = 0. Приравнивание к нулю определителя матрицы L* приводит к уравнению 8-го порядка для k.
надо принять ρfl = 0. Приравнивание к нулю определителя матрицы L* приводит к уравнению 8-го порядка для k.
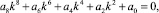 (15)
(15)
коэффициенты которого очевидным образом получаются из (14).
При отсутствии жидкости левая часть является многочленом 8 порядка, а при наличии жидкости – нет, так как коэффициенты a4, a2 и a0 зависят от k.
Для оболочки с жидкостью обсудим вопрос об аппроксимации при k ≥ 0 выражения
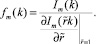 (16)
(16)
Разложение функции (16) в ряд Тейлора по степеням k при m = 1, 2, 3…позволяет при малых k в качестве нулевого приближения взять, как это принято в [4],
f(k) = 1/m. (17)
Однако для k по модулю больших 1 недостаточно даже трёх первых ненулевых членов разложения (то есть до k4), ибо отбрасываемая часть не будет являться малой, а взять большее количество членов ряда не позволяет 8-й порядок уравнения (15).
Расчёт при точных значениях fm(k) возможен с помощью применения схемы итерационного типа, когда при нахождении k на последующем по ω шаге в fm(k) вводятся значения k с предыдущего шага, а значения k при ω = 0 по-прежнему являются корнями многочлена 8 степени, так как при ω = 0, для любого m = 1, 2, 3, … 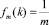 . Однако такой расчёт требует больших вычислительных ресурсов. Поэтому предлагается достаточно простая аппроксимация (18) для fm(k), не отменяющая итерационной схемы, но более экономная по ресурсам. Она получена чисто эмпирическим путём:
. Однако такой расчёт требует больших вычислительных ресурсов. Поэтому предлагается достаточно простая аппроксимация (18) для fm(k), не отменяющая итерационной схемы, но более экономная по ресурсам. Она получена чисто эмпирическим путём:
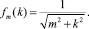 (18)
(18)
Близость получающихся при этом значений fm(k) при m = 1 и m = 2 иллюстрирует рис. 1.
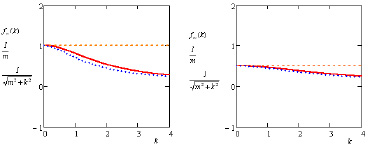
Рис. 1. Точные значения fm(k) – красная сплошная линия, нулевое приближение – оранжевая пунктирная линия, предлагаемое приближение – синяя точечная линия. Слева при m = 1; справа при m = 2
На рис. 2–4 приведены корни уравнения (15) при m = 1, 2, 3 для точных значений fm(k), приближенных по формуле (17), и приближенных по формуле (18). В расчетах принималось 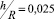 ,
, 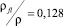 . При использовании точных значений fm(k) и приближенных по (18) получаются близкие дисперсионные кривые, неразличимые в масштабах графиков. Сопоставление их с кривыми, полученными с помощью нулевого приближения, показывает, что частоты, на которых зарождаются распространяющиеся волны (появляются чисто мнимые осевые волновые числа k), успешно определяются в том и в другом случае, слегка меняется лишь форма ветвей дисперсионных кривых. Зато частоты отсечки затухающих волн (исчезновение полностью комплексных осевых волновых чисел) меняются существенно. Поэтому вряд ли следует пренебрегать упомянутыми выше уточнениями в компонентах матрицы, связанных с наличием жидкости. Для сравнения на всех рис. 2–4 приводятся дисперсионные кривые для оболочки без жидкости. Для компактности приводятся только положительные значения вещественных и мнимых частей, отрицательные просто имеют противоположный знак. Отметим, что распространяющимся в направлении оси ox волнам соответствуют чисто мнимые волновые числа со знаком « + », волнам, затухающим в направлении ox, – полностью комплексные волновые числа с отрицательной вещественной частью и положительной мнимой, а затухающим в направлении ox неволновым перемещениям соответствуют чисто вещественные отрицательные волновые числа. На рис. 2–4 красной линией обозначены k для оболочки с жидкостью при fm(k) по формуле (17), синей – для оболочки с жидкостью при fm(k) по формуле (18), зелёной – для оболочки без жидкости. Вещественные и мнимые части полностью комплексных k изображены сплошной линией, а чисто вещественные и чисто мнимые корни – пунктирной.
. При использовании точных значений fm(k) и приближенных по (18) получаются близкие дисперсионные кривые, неразличимые в масштабах графиков. Сопоставление их с кривыми, полученными с помощью нулевого приближения, показывает, что частоты, на которых зарождаются распространяющиеся волны (появляются чисто мнимые осевые волновые числа k), успешно определяются в том и в другом случае, слегка меняется лишь форма ветвей дисперсионных кривых. Зато частоты отсечки затухающих волн (исчезновение полностью комплексных осевых волновых чисел) меняются существенно. Поэтому вряд ли следует пренебрегать упомянутыми выше уточнениями в компонентах матрицы, связанных с наличием жидкости. Для сравнения на всех рис. 2–4 приводятся дисперсионные кривые для оболочки без жидкости. Для компактности приводятся только положительные значения вещественных и мнимых частей, отрицательные просто имеют противоположный знак. Отметим, что распространяющимся в направлении оси ox волнам соответствуют чисто мнимые волновые числа со знаком « + », волнам, затухающим в направлении ox, – полностью комплексные волновые числа с отрицательной вещественной частью и положительной мнимой, а затухающим в направлении ox неволновым перемещениям соответствуют чисто вещественные отрицательные волновые числа. На рис. 2–4 красной линией обозначены k для оболочки с жидкостью при fm(k) по формуле (17), синей – для оболочки с жидкостью при fm(k) по формуле (18), зелёной – для оболочки без жидкости. Вещественные и мнимые части полностью комплексных k изображены сплошной линией, а чисто вещественные и чисто мнимые корни – пунктирной.
Рис. 2–4 приводят к следующим выводам для рассмотренного диапазона частот.
При m = 1 затухающие волны зарождаются при ω = 0 и прекращаются при ω = 0,420.42; 0,74; 1,02 соответственно для каждого случая (с жидкостью по (17), с жидкостью по (18), без жидкости). Первые две распространяющиеся волны зарождаются при ω = 0 и ω = 0,61, одинаковых для всех случаев, а третья – при ω = 1,09; 1,09; 1,4 соответственно.
При m = 2 две затухающие волны зарождаются при ω = 0, первая прекращается при ω = 0,011; 0,011; 0,019, а вторая прекращается при ω = 0,59; 0,83; 1,10 соответственно для каждого случая. Две распространяющиеся волны в рассмотренном диапазоне частот зарождаются: первая при ω = 0,011; 0,011; 0,019 соответственно для каждого случая, а вторая при ω = 1,20, одинаковых для всех рассмотренных случаев.
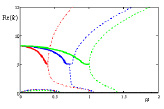
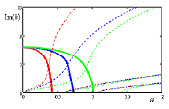
Рис. 2. Осевые волновые числа k при m = 1 (балочные колебания) в зависимости от частоты ω
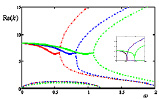
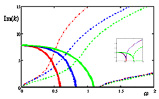
Рис. 3. Осевые волновые числа k при m = 2 (неосесимметричные колебания) в зависимости от частоты ω. На внутреннем рисунке те же кривые при малых ω до 0,03
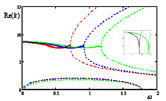
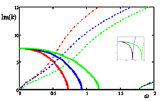
Рис. 4. Осевые волновые числа k при m = 3 (неосесимметричные колебания) в зависимости от частоты ω. На внутреннем рисунке те же кривые при малых ω до 0,06
При m = 3 две затухающие волны зарождаются при ω = 0 и прекращаются: первая при ω = 0,035; 0,035; 0,055; вторая при ω = 0,73; 0,93; 1,18 соответственно для каждого случая. Две распространяющиеся волны в рассмотренном диапазоне частот зарождаются: первая при ω = 0,034; 0,034; 0,054 соответственно для каждого случая; вторая при ω = 1,79, одинаковых для всех рассмотренных случаев.
Отметим, что в [5] аналогичная задача рассмотрена для ортотропной оболочки.
Рецензенты:
Фёдоров А.С., д.т.н., профессор кафедры сопротивления материалов Санкт-Петербургского государственного морского технического университета, г. Санкт-Петербург;
Хазанов В.Б., д.ф.-м.н., профессор кафедры прикладной математики Санкт-Петербургского государственного морского технического университета, г. Санкт-Петербург.
Работа поступила в редакцию 26.07.2013.



