Согласно [1], основным этапом проектирования современных систем физической защиты (СФЗ) является стадия концептуального проектирования СФЗ промышленного объекта. При этом одной из главных задач концептуального проектирования выступает обоснование и выбор рациональных структуры и состава разрабатываемого комплекса инженерно-технических средств (КИТС) СФЗ промышленного объекта, по сути определяющих решение задач по нахождению [10]:
1) топологии, задающей расстановку и смежность между узлами комплекса (подступами к объекту N1, рубежами защиты N2 и охраняемыми зонами N3) с учетом ограничения на существование путей (доступа) от подступов до объекта к определенным зонам охраны;
2) плана установки на рубежах защиты различных инженерно-технических средств охраны (ИТСО).
Цель статьи заключается в разработке алгоритма структурно-параметрического синтеза КИТС СФЗ промышленного объекта. Необходимо отметить, что настоящая статья является продолжением работы [11], и полноценное понимание изложенных здесь результатов затруднительно без предварительного ознакомления с указанной публикацией.
Формальная постановка задачи синтеза
В [11] сформирована математическая модель КИТС СФЗ, позволяющая задать аналитическую зависимость между рентабельностью синтезируемого КИТС СФЗ (показателем эффективности) и структурно-функциональными свойствами, характеризующими: структуру, определяющую топологические связи между подступами к объекту, рубежами защиты и охраняемыми зонами; различные способы преодоления рубежей защиты; разнородность ИТСО по принципу действия, обеспечивающих разноэффективный уровень защиты рубежа от конкретных способов его преодоления; стоимость ИТСО; ограничение на допустимую стоимость устанавливаемых ИТСО, необходимых для решения задачи по нахождению рациональных топологий КИТС СФЗ и плана установки на рубежах защиты различных ИТСО. Согласно заданным в [11] представлениям, обобщенный критерий эффективности КИТС СФЗ определяется в виде
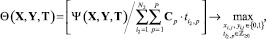 (1)
(1)
где 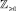 – множество неотрицательных целых чисел: {0, 1, 2, ...}; Сp – суммарная стоимость ИТСО по их установки, эксплуатации и т.д.; Ψ(X, Y, T) – функция, преобразующая пространство матриц управляющих переменных, характеризующих топологическую структуру
– множество неотрицательных целых чисел: {0, 1, 2, ...}; Сp – суммарная стоимость ИТСО по их установки, эксплуатации и т.д.; Ψ(X, Y, T) – функция, преобразующая пространство матриц управляющих переменных, характеризующих топологическую структуру 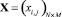 ,
, 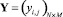 и состав (план установки ИТСО)
и состав (план установки ИТСО) 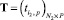 , в выходной параметр – обратную величину суммарного вероятного уровня ущерба (риска) КИТС СФЗ. Матрицы управляющих переменных X и Y определяют «…соответствующие элементы матриц инцидентности для прямого Hin и обратного Hout потоков синтезируемой структуры СФЗ» [11]. Элементы матрицы T характеризуют количество устанавливаемых на i2-м рубеже защиты p-х типов ИТСО.
, в выходной параметр – обратную величину суммарного вероятного уровня ущерба (риска) КИТС СФЗ. Матрицы управляющих переменных X и Y определяют «…соответствующие элементы матриц инцидентности для прямого Hin и обратного Hout потоков синтезируемой структуры СФЗ» [11]. Элементы матрицы T характеризуют количество устанавливаемых на i2-м рубеже защиты p-х типов ИТСО.
В общем виде сформированная задача синтеза (1) в [11] относится к классу задач дискретной оптимизации [7]. При этом в связи с различием областей определения значений элементов матриц управляющих переменных 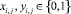 ,
, 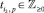 и многомерностью оптимизируемой целевой функции (1) совместное решение задач структурного и параметрического синтеза КИТС СФЗ промышленного объекта за полиномиальное время с использованием известных подходов не представляется возможным, поскольку использование класса комбинаторных алгоритмов для решения подобных дискретных задач порождает значительную вычислительную сложность. Принципиальным результатом исследования таких задач является понятие полной задачи [9].
и многомерностью оптимизируемой целевой функции (1) совместное решение задач структурного и параметрического синтеза КИТС СФЗ промышленного объекта за полиномиальное время с использованием известных подходов не представляется возможным, поскольку использование класса комбинаторных алгоритмов для решения подобных дискретных задач порождает значительную вычислительную сложность. Принципиальным результатом исследования таких задач является понятие полной задачи [9].
Последовательное решение задач по
1) нахождению рациональной структуры КИТС СФЗ на заданном исходном плане установки ИТСО T*, определяемой
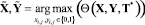 ;
;
2) оптимизации плана установки ИТСО (параметров КИТС СФЗ) на рубежах защиты
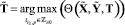
с учетом найденной на первом этапе рациональной структуры, – теоретически обеспечивает существенное снижение вычислительных затрат.
Однако наряду с относительным уменьшением вычислительной сложности последовательное решение задач синтеза не позволяет:
1) определить точку
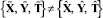 ,
,
соответствующую глобальному оптимуму целевой функции (1);
2) решить вопрос о корректности выбора исходного плана установки ИТСО T* на первом этапе решения задачи синтеза;
3) произвести решение задачи структурного и параметрического синтеза за полиномиальное время.
Для уменьшения вычислительной сложности расширим класс используемых алгоритмов при решении общей задачи (1) структурно-параметрического синтеза. Другими словами, представим исходную комбинаторную задачу как общую задачу нелинейного программирования, т.е. по существу используем условный подход, идея которого указана в [6] и основана на полиномиальной сводимости языка 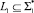 (
(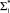 – алфавит языка L1) исходной дискретной оптимизационной задачи к языку
– алфавит языка L1) исходной дискретной оптимизационной задачи к языку 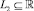 – непрерывной (¡ – множество вещественных чисел). Достаточным условием полиномиальной сводимости L1∞L2, согласно [6] является существование функции реализации такой сводимости
– непрерывной (¡ – множество вещественных чисел). Достаточным условием полиномиальной сводимости L1∞L2, согласно [6] является существование функции реализации такой сводимости 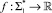 , удовлетворяющей условиям:
, удовлетворяющей условиям:
1. Существует детерминированная однолинейная машина Тьюринга, вычисляющая f с временной сложностью, ограниченной полиномом.
2. Для любого 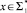 , x ∈ L1 в том и только том случае, если f(x) ∈ L2.
, x ∈ L1 в том и только том случае, если f(x) ∈ L2.
Существенная важность понятия полиномиальной сводимости, необходимой для формирования полиномиального алгоритма структурно-параметрического синтеза КИТС СФЗ, следует из леммы, описанной и доказанной в [6]: «Лемма. Если L1∞L2, то из L2 ∈ P следует, что L1 ∈ P. (Эквивалентно утверждение: из L2 ∉ P следует, что L1 ∉ P)».
С этой целью определим функции f1(x) и f2(x), удовлетворяющие двум указанным условиям и реализующие полиномиальную сводимость 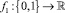 для элементов матриц управляющих переменных
для элементов матриц управляющих переменных 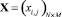 и
и 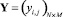 , т.е. структурный синтез, и
, т.е. структурный синтез, и 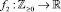 для элементов матриц
для элементов матриц 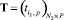 , т.е. параметрический синтез.
, т.е. параметрический синтез.
Для задания функции f1(x), определяющей отображение 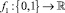 , используем свойство идемпотентности [7]: x2 = x, допускающее булевость переменной x (x = 0 или 1). Функцию f2(x), задающую отображение
, используем свойство идемпотентности [7]: x2 = x, допускающее булевость переменной x (x = 0 или 1). Функцию f2(x), задающую отображение 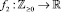 , представим с помощью введения в исходную задачу (1) дополнительных целочисленных ограничений, записанных с помощью элементарных тригонометрических функций, к примеру [12], sin(π∙x) = 0.
, представим с помощью введения в исходную задачу (1) дополнительных целочисленных ограничений, записанных с помощью элементарных тригонометрических функций, к примеру [12], sin(π∙x) = 0.
Применение подобных представлений позволяет изменить класс исходной оптимизационной задачи (1) c дискретной на нелинейную и преобразовать формальную постановку структурно-параметрического синтеза КИТС СФЗ к виду
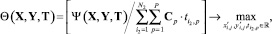 (2)
(2)
с учетом ограничений [11]:
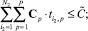 (3)
(3)
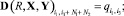
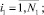
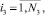 (4)
(4)
и дополнительных ограничений на булевость и целочисленность переменных:
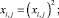
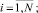
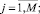 (5)
(5)
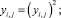
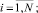
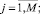 (6)
(6)
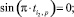
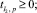
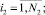
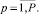 (7)
(7)
В выражениях (3), (4) 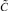 – максимально допустимая стоимость ИТСО (установка, эксплуатация и т.д.);
– максимально допустимая стоимость ИТСО (установка, эксплуатация и т.д.); 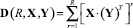 – матрица достижимости для всех возможных путей кратности от 1 до R.
– матрица достижимости для всех возможных путей кратности от 1 до R.
Таким образом, целочисленная задача (1) преобразована в общую задачу нелинейного программирования (2)–(7) путем введения дополнительных ограничений (5)–(7). Такая ситуация обусловливает возможность решения сформированной нелинейной задачи с использованием релаксационных градиентных методов [4] при минимальном количестве предположений. Однако многомерность оптимизируемой целевой функции, где число переменных определяется как 2∙M∙N + N2∙P (M и N – число ребер и вершин в исходном графе [11] соответственно), приводит к росту вычислительных затрат при решении задачи методами градиентной оптимизации первого порядка (градиентный спуск, наискорейший спуск, сопряженных градиентов Флетчера‒Ривса, Полока‒Райбера и др.). Повышение скорости сходимости алгоритма возможно обеспечить применением методов оптимизации второго порядка (Ньютона, Ньютона-Рафсона, Марквардта, Левенберга‒Марквардта и др.). Однако использование последних накладывает более жесткие требования на определение начальных приближений оптимизационного алгоритма. Это связано с тем, что методы второго порядка являются менее устойчивыми, чем, например, методы сопряженных градиентов, и имеют тенденцию «застревать» в локальных минимумах [4], а также требуют больших вычислительных затрат на единичной итерации, связанных с необходимостью вычисления матрицы вторых частных производных (матрицы Гессе) и ее обращения (псевдообращения) [4, 7]. С целью устранения указанного противоречия между высокой скоростью сходимости, достигаемой методами второго порядка, и устойчивостью, обеспечиваемой методами сопряженных градиентов, согласно [12] приведем сформированный критерий (2) с учетом положений теории геометрии центров масс [3] и представлений, заданных в [2], к виду
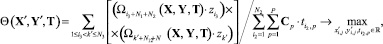 (8)
(8)
где Ω(X, Y, T) – векторная функция, обратная величине действительного риска размерности N, элементы которой задают вероятность защиты от угрозы i-х узлов КИТС СФЗ с учетом воздействий ИТСО (субъектов защиты) на злоумышленника (субъект угрозы) [11]; 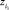 – значимость i3-х охраняемых зон.
– значимость i3-х охраняемых зон.
Сформированная целевая функция (8), отражающая критерий максимума моментов инерции, в соответствии с [2] позволяет повысить скорость сходимости алгоритма структурно-параметрического синтеза при использовании градиентных методов с переменной метрикой, обусловленное снижением ранга матрицы Гессе за счет увеличения линейной зависимости ее строк.
Алгоритм структурно-параметрического синтеза КИТС СФЗ
Ввиду многомерности оптимизируемой целевой функции (8); наличия большого числа ограничений, накладываемых на переменные; периодичности функций-ограничений, эффективность работы алгоритма существенно зависит от выбора начальных приближений. В этой связи поиск начальных приближений переменных {X*, Y*, T*} предлагается осуществить путем следующей поэтапной декомпозиции:
1) решить задачу параметрического синтеза для топологии, заданной полносвязным графом 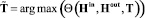 ;
;
2) на основе сформированного плана установки ИТСО определить структуру КИТС СФЗ 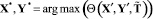 ;
;
3) осуществить оптимизацию плана установки ИТСО 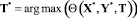 с учетом найденной рациональной структуры, что обусловливает необходимость разработки частных алгоритмов параметрического и структурного синтеза КИТС СФЗ промышленного объекта.
с учетом найденной рациональной структуры, что обусловливает необходимость разработки частных алгоритмов параметрического и структурного синтеза КИТС СФЗ промышленного объекта.
В общем виде задача параметрического синтеза КИТС СФЗ промышленного объекта сводится к нахождению оптимума целевой функции:
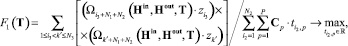 (9)
(9)
с учетом ограничений (3), (7).
Максимизация сформированной целевой функции F1(T) с учетом ограничений в виде равенств и неравенств произведена на основе метода штрафных функций [4] путем сведения задачи условной максимизации к решению последовательности задач поиска безусловного максимума вспомогательной функции:
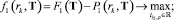
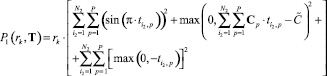 , (10)
, (10)
где P1(rk, T) – штрафная функция; rk – коэффициент штрафа.
На каждой k-й итерации осуществляется поиск точки с координатами 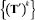 , доставляющей максимум вспомогательной функции f1(rk, T) при заданном параметре штрафа rk методом сопряженных градиентов с переменной метрикой Дэвидона–Флетчера–Пауэлла, стратегия которого подробно рассмотрена в [4].
, доставляющей максимум вспомогательной функции f1(rk, T) при заданном параметре штрафа rk методом сопряженных градиентов с переменной метрикой Дэвидона–Флетчера–Пауэлла, стратегия которого подробно рассмотрена в [4].
Задача структурного синтеза КИТС СФЗ промышленного объекта сводится к нахождению оптимума целевой функции:
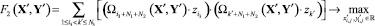 (11)
(11)
с ограничениями (4)–(6).
Нахождение условного экстремума (11) выполнено по аналогии с решением задачи параметрического синтеза методом штрафных функций на каждой итерации штрафа [4], при этом безусловная вспомогательная целевая функция задана в виде
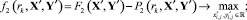
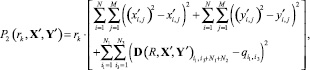 (12)
(12)
с осуществлением решения безусловной задачи (13) на каждой k-й итерации штрафа методом Дэвидона–Флетчера–Пауэлла.
Решение задачи структурно-параметрического синтеза КИТС СФЗ, заданной в виде целевой функции (8) с учетом ограничений (3)–(7), выполнено методом штрафных функций, при этом вспомогательная функция задана в виде разности целевой Θ(X′, Y′, T) (8) и штрафной P(rk, X′, Y′, T) функций:
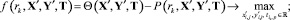
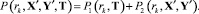 (13)
(13)
Для оценки эффективности работы предложенного алгоритма проведен ряд вычислительных экспериментов, в ходе которых произведен анализ результативности разработанного алгоритма и вычислительной сложности. В связи с выбранным критерием эффективности КИТС СФЗ промышленного объекта (1), заданным по правилу «отношения максимума защищенности (минимум риска) и минимума стоимости», для оценки результативности решения определим рентабельности синтезируемого КИТС СФЗ промышленного объекта по алгоритмам:
1) параметрического синтеза, предложенного в [12];
2) последовательного параметрического и структурного синтеза;
3) раздельного синтеза по схеме «параметрический-структурный-параметрический синтез»;
4) структурно-параметрического синтеза в рамках проведения математико-алгоритмического эксперимента. В результате оценки получен график зависимости рентабельности синтезируемого по указанным алгоритмам КИТС СФЗ промышленного объекта от числа узлов, задающих максимальное количество рубежей защиты N2 (рисунок, а).
а 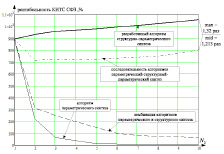 б
б 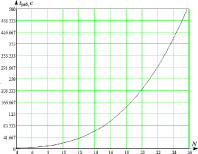
Оценка эффективности разработанного алгоритма структурно-параметрического синтеза КИТС СФЗ, включающая определение: а – зависимости рентабельности синтезируемого КИТС СФЗ промышленного объекта от числа рубежей защиты N2; б – асимптотической оценки вычислительной сложности
В [8] для расчета вычислительной сложности используется «O оценка» сложности алгоритмов, определяющая функцию g(N) порядка роста времени работы алгоритма. Определение вычислительной сложности сформированных алгоритмов производилось путем их реализации на языке программирования С++ в интегрированной среде программирования CodeGear RAD Studio XE2 с последующим проведением ряда вычислительных экспериментов, определяющих время работы алгоритма на «наихудший случай» [8] для погрешности вычислений ε = 10–7 на ЭВМ с характеристиками: Intel(R) Xeon(TM) CPU 3.60 GHz, 3.60 GHz; 2 Gb ОЗУ; жесткий диск 200 Gb. Результаты экспериментов для разработанного алгоритма представлен на рисунке, б (N – общее количество элементов синтезируемого комплекса).
Выводы
Таким образом, разработанный алгоритм структурно-параметрического синтеза с учетом представлений, предложенных в [11], реализует совместное решение по нахождению рациональных топологической структуры и состава КИТС СФЗ. При этом совместное решение позволяет повысить рентабельность проектируемой системы в среднем на величину порядка 1,213 раз по сравнению с существующими последовательными решениями. В общем случае применение идемпотентных x2 = x и целочисленных sin(π∙x) = 0 ограничений в классе подобных задач синтеза позволяет осуществить преобразование комбинаторной постановки (1) в общую задачу нелинейного программирования (2). Представленные экспериментальные результаты по оценке вычислительной сложности (см. рисунок, б) разработанного алгоритма подтверждают, что предложенный в статье подход к решению задачи структурно-параметрического синтеза позволяет значительно снизить вычислительные затраты на поиск рациональных структуры и состава КИТС СФЗ. Следует отметить, что для решения подобных задач нелинейного программирования (2) с учетом ограничений (3)–(7) применение метода множителей Лагранжа [4] является нецелесообразным. Это объясняется тем, что введение дополнительных переменных, сводящих целевую функцию и ограничения в виде равенств и неравенств в общий полином Лагранжа, приводит к резкому увеличению числа переменных в итоговой безусловной оптимизационной задаче. Последнее обусловливает существенное повышение вычислительных затрат и определяет сложность процедуры поиска его начальных приближений. Такая ситуация обусловливает предпочтительность использования метода штрафных функций.
Рецензенты:
Архипов Н.С., д.т.н., доцент, сотрудник Академии СФО России, г. Орёл;
Иванов Б.Р., д.т.н., профессор, сотрудник Академии СФО России, г. Орёл.
Работа поступила в редакцию 23.08.2013.



