В современной психолого-педагогической литературе большое внимание уделяется выявлению факторов, влияющих на успеваемость студентов, например [6–8]. Для получения численных характеристик влияния изучаемых параметров на успеваемость применяются методы корреляционного анализа (коэффициенты корреляции r-Пирсона, r-Спирмена и τ-Кендалла), факторный, таксонометрический анализ и другие методы статистического анализа [5, 10]. Несмотря на большое количество публикаций, посвящённых указанной тематике, по мнению профессора С.Д. Смирнова [10]: «...в современной психологии образования недостает комплексных исследований факторов, влияющих на успешность обучения в высшей школе, недостаточно разработаны вопросы о связи способностей с успеваемостью студентов, а также ограничены возможные выводы из традиционных корреляционных исследований».
Проблематичность получаемых выводов связана ещё и с тем, что зачастую результаты, полученные при тестировании определённой выборки студентов, оказываются недействительными даже для отдельных студентов той же выборки. В связи с этим представляет очевидный интерес выявить возможные факторы, влияющие на ограничение адекватности исследований. В публикации профессора МГУ А. Шмелёва [12] акцентируется внимание на валидность тестов, которая: «...обозначает, насколько точно тест выявляет именно то психическое свойство, на измерение которого он направлен». Там же отмечается, что исследователь должен чётко представлять, что измеряет. От себя можно добавить, что существенным моментом является не только чёткое понимание того, что измеряется, но и то, с чем сравниваются результаты тестирования.
В предлагаемой работе предполагается проанализировать и уточнить использование понятия «Средняя успеваемость студентов». Наиболее часто под успеваемостью подразумевают средние значения оценок, полученных студентом за определённый период времени. При кредитной технологии обучения в качестве показателя успеваемости используется средневзвешенная оценка уровня достижений (GPA – Grade Point Average), определяющая интервальные значения баллов, имеющих соответствие с классической системой оценки знаний. Другими словами, оценки, получаемые студентами, представляют собой определённые характеристики, выставляемые разными преподавателями, выступающими в роли экспертов. Совокупность выставленных отдельному студенту оценок подчиняется непараметрической статистике.
С другой стороны, для получения статистически значимых результатов необходима достаточно большая выборка студентов, объём которой зависит от размерности изучаемого факторного пространства. В результате возникает естественная потребность перехода от непараметрической статистики, описывающей успеваемость отдельного студента, к параметрической статистике выборки, на основе анализа результатов тестирования делаются выводы о значимости изучаемых факторов. Из параметрических методов наиболее широко используется нормальное или гауссово распределение. Суходольский Г.В. отмечает, что [11, С. 120] «...в психологических дисциплинах его значение трудно переоценить. Достаточно сказать, что все психологические шкалы основываются на этом законе, поскольку ему следует распределения большинства человеческих способностей и свойств». Тем не менее, несколько далее [11, С. 131] подчёркивается важность нормализации распределений (их отображения в нормальное распределение). В этой же работе выделяются три метода нормализации: в эксперименте, преобразованием переменной, а также по составу. Отмечается, что все методы весьма трудоёмки и не всегда обеспечивают желаемые результаты.
Это означает косвенное признание того факта, что полученные в ходе психологических исследований результаты часто не подчиняются нормальному распределению, что ставит под сомнение возможность применения статистических методов для адекватной интерпретации результатов. Таким образом, намечается противоречие между статистическим инструментарием, требующим нормальности распределения выборки и реальными характеристиками исследуемых выборок. Учитывая важность исполнения данного условия, С.И. Архангельский [2, С. 79] дает прямую рекомендацию: «Использование в функциональных моделях статистических методов предполагает нормальное распределение индивидуальных вариаций изучаемых переменных».
Сопоставляя приведённые выше высказывания, можно заподозрить, что требования приведения полученных данных в соответствие с нормальным законом распределения вызвано только желанием использовать глубоко проработанные статистические методы исследований. К выводу о том, что реальные законы, управляющие поведением людей, сложнее, чем описываемые нормальным законом распределения, пришли авторы работы [4, С. 4], М.И. Грабарь и К.А. Краснянская: «...теоретические вероятностные законы для большинства педагогических явлений неизвестны...» В работе [3, С. 52–53] Б.П. Битинасом высказывается тезис о том, что: «... теряет почву предположение о нормальном распределении уровней психических свойств личности» и подвергаются критике методика нормализации распределений. Приведённые противоречивые высказывания различных авторов свидетельствуют о наличии проблем, связанных с применением статистических методов для обработки психолого-педагогических экспериментов.
В создании модели, связывающей психолого-физиологические характеристики студентов, с их средней успеваемостью обычно участвует тест, определяющий характеристики изучаемого факторного пространства и показатели средней успеваемости. В соответствии с изложенным выше материалом, обработка результатов исследований должна начинаться со статистического анализа левой и правой части модели.
Анализ успеваемости студентов на соответствие нормальному закону, проведённый в работе [1], показал, что:
«Количество групп, в которых эмпирические распределения соответствуют нормальному закону, существенно меняется в зависимости от показателя успеваемости. Нормальному распределению в наибольшей степени подчиняются среднегодовая текущая успеваемость, а в наименьшей – результаты годового экзамена».
Из этого следует, что переход от непараметрической статистики успеваемости отдельного студента к параметрической статистике успеваемости большой группы студентов оказывается не вполне тривиальным. Вполне понятно, что наличие неопределённостей, неоднозначностей в исходных данных, используемых для построения модели, может значительно затруднить или свести на нет все попытки создания самой модели. Поэтому приведённые выше наблюдения требуют некоторого осмысления.
|
Номер интервала |
Данных в интервале |
Нижняя граница интервала |
Средн. усп. в интерв. |
Теоретич. кол-во |
Расчёт Хи-квадрат |
|
1 |
8 |
3,130 |
2,947 |
7,231 |
0,0818 |
|
2 |
10 |
3,427 |
3,318 |
10,282 |
0,0077 |
|
3 |
10 |
3,538 |
3,493 |
5,572 |
3,5190 |
|
4 |
10 |
3,793 |
3,633 |
15,997 |
2,2483 |
|
5 |
10 |
3,930 |
3,868 |
9,914 |
0,0007 |
|
6 |
10 |
4,000 |
3,974 |
5,179 |
4,4880 |
|
7 |
10 |
4,188 |
4,079 |
13,723 |
1,0102 |
|
8 |
10 |
4,375 |
4,286 |
12,326 |
0,4391 |
|
9 |
10 |
4,621 |
4,458 |
12,588 |
0,5321 |
|
10 |
10 |
4,841 |
4,752 |
7,349 |
0,9563 |
|
11 |
10 |
5,000 |
4,955 |
7,839 |
0,5958 |
|
Всего: |
108 |
Средн. успев: |
3,978 |
Хи-квад: |
13,88 |
В статистике имеется ряд теорем под общим обозначением «центральная предельная теорема», определяющих условия, при которых суммы, средние значения и т.п. имеют распределения вероятностей, близкие к нормальному закону распределения. Известно, что средняя успеваемость студентов относится к непараметрической статистике и на основании классической центральной предельной теоремы утверждается, что бесконечная последовательность независимых одинаково распределённых случайных величин с конечной дисперсией имеет среднее значение, подчиняющееся распределению, близкому к нормальному. При невыполнении условия одинаковой распределённости на последовательность случайных величин накладывается требование отсутствия доминирования какого-либо слагаемого, и вклад каждого слагаемого в среднее арифметическое должен быть пренебрежимо мал по сравнению с итоговой суммой (теоремы П.Л. Чебышева, А.А. Маркова, А.М. Ляпунова, …). Можно выдвинуть предположение о том, что отмеченные в [1] особенности связаны с нарушением упомянутых выше ограничений.
Для ответа на возникшие вопросы и сомнения была сформирована случайная выборка студентов очной, заочной и дистанционной форм обучения (11 академических групп 2–4 курса, 108 человек), с количеством студентов в группе, случайным образом варьирующимся от четырёх до девятнадцати человек. Количество оценок участвующих в расчёте средней успеваемости отдельного студента колебалось в интервале от тринадцати до сорока двух.
В приводимых расчётах участвовало 2658 оценок успеваемости, включающих: 1095 –«отлично», 750 – «хорошо», 731 – «удовлетворительно» и 82 – «неудовлетворительно». Средняя успеваемость в выборке – 3,98 баллов.
Проверка на нормальность распределения полученной выборки средней успеваемости студентов проводилась при помощи критерия Хи-квадрат (таблица). Для выполнения проверки данные были отсортированы по возрастанию и полученный вариационный ряд разделён на одиннадцать интервалов. Исходные данные были искусственно разделены на подгруппы по десять человек. При этом первая группа с наиболее слабой успеваемостью по остаточному принципу содержала восемь значений. Теоретические значения количества студентов в интервалах при условии выполнения закона нормального распределения случайной величины отображены в столбце 5 (таблица). Критическое значение критерия Хи-квадрат (при вероятности P = 95 % и числе степеней свободы f = 8) равно 15,51. Так как полученное значение (13,88) меньше критического, гипотезу о нормальности полученного распределения следует принять. Построим зависимость интервального значения стандартного отклонения в интервале от средней успеваемости в том же интервале (рисунок). Полученный график имеет хорошо выраженную зависимость между рассматриваемыми параметрами и асимптотически приближается к значению средней выборочной дисперсии, характерной для большей части выборки.
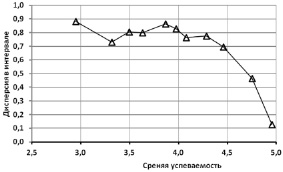
Зависимость выборочной дисперсии в интервале от значения средней успеваемости в интервале
По критерию стандартного отклонения случайной величины можно выделить два класса студентов:
1. Класс со средней успеваемостью L ≤ 4,38, для которого наблюдаются близкие (в данном случае к Y ≈ 0,8) значения выборочной дисперсии. Расчёт показывает наличие слабой линейной зависимости
Y1 = 0,9079 – 0,0267x,
которая незначима с точки зрения рассматриваемых нами проблем.
2. Класс со средней успеваемостью L ≥ 4,38, для которого выборочная дисперсия имеет определённую функциональную зависимость от средней успеваемости (в данном случае
Y2 = –1,462x2 + 12,536x – 26,11.
В граничной точке (L = 4,38) значения уравнения линии тренда Y2 = 0,750 согласуются с выборочной дисперсией остальной выборки. По нашему представлению, этот результат имеет вполне очевидную причину – в оценках студентов по мере увеличения средней успеваемости выше L = 4,38 происходит увеличение количества отличных оценок и резкое сокращение троек и четвёрок, что и способствует понижению вплоть до нулевого значения (для абсолютных отличников) стандартного отклонения средней успеваемости студента. Наличие аналогичного эффекта можно было бы предполагать и во второй пограничной зоне (средняя успеваемость около трёх баллов), но она, вероятно, буферируется за счёт неуспевающих студентов, не успевших к моменту снятия данных пересдать (или просто сдать) контрольное мероприятие.
Представленные выше результаты позволяют сделать ряд выводов:
1. Несмотря на то, что значение критерия Хи-квадрат не отвергает гипотезу о нормальности полученного распределения, можно утверждать, что любая выборка не будет подчиняться распределению Гаусса в связи с наличием функциональной зависимости дисперсии от значения средней успеваемости студентов.
2. Результаты пересдач неудовлетворительных оценок могут искажать параболическую форму кривой зависимости дисперсии от средней успеваемости.
3. Предполагается нецелесообразным применение предельного перехода от непараметрической статистики отдельных студентов к параметрической статистике общей выборки студентов без предварительного выделения подгруппы студентов, отвечающих условиям применимости предельной теоремы.
В дополнении к приведённым выводам возникает ещё и ряд дополнительных вопросов:
- Как обрабатывать результаты, не отвечающие требованию равнораспределённости?
- Может ли функция, описывающая распределение случайных ошибок измерения, быть достаточно информативной для описания факторов мотивации студентов к обучению?
- Можно ли разброс показателей успеваемости студентов трактовать как ошибку выборочного среднего и считать, что разброс объясняется только стечением случайных обстоятельств?
- Как относиться к тому, что вблизи граничных значений успеваемости нарушается симметричность распределения ошибки среднего (за границами предельного балла значений нет)?
- Имеются ли ограничения для расчётов доверительных границ оценки средней успеваемости с использованием распределения Стьюдента?
- Как относиться к статистическим критериям отбраковки выделяющихся значений?
- Как реагировать на систематическое уменьшение дисперсии для студентов – отличников и является ли «растворение» этих данных в массе других оценок полезным и целесообразным для целей анализа?
Рецензенты:
Бухарова Г.Д., д.п.н., профессор кафедры информационных технологий, ФГАОУ ВПО «Российский государственный профессионально-педагогический университет», г Екатеринбург;
Долинер Л.И., д.п.н., заведующий кафедрой информационных технологий, ГБОУ ДПО Свердловской области «Институт развития образования», г. Свердловск.
Работа поступила в редакцию 07.08.2013.



