Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

В настоящее время в процессе оптимизации параметров сложных систем [2] все чаще применяются природные механизмы поиска [6]; интенсивно разрабатывается научное направление Natural Computing – «Природные вычисления», к которым можно отнести:

• Genetic Algorithms – генетические алгоритмы;
• Evolution Programming – эволюционное программирование;
• Neural Network Computing – нейросетевые вычисления;
• DNA Computing – ДНК-вычисления;
• Cellular Automata – клеточные автоматы;
• Ant Colony Algorithms– муравьиные алгоритмы.
• Прочие алгоритмы роевого интеллекта.

Цель исследования. В данной работе отражены результаты исследований двух эвристических алгоритмов: генетического и муравьиного, которые проводились на примере задачи поиска наименьшего гамильтонова цикла в полном графе (кратчайшего замкнутого маршрута, проходящего через все его вершины), оценена целесообразность использования того или иного метода, а также исследована эффективность работы эвристических алгоритмов с применением разработанных модификаций.

Генетический алгоритм (ГА) – эвристический алгоритм, постепенно улучшающий некоторое текущее приближенное решение путём случайного подбора, комбинирования и вариации искомых параметров с использованием механизмов, напоминающих биологическую эволюцию.

В процессе исследования были разработаны следующие модификации ГА: «модификация жадным алгоритмом», «несколько популяций» и «модификация методом ветвей и границ». Они ускоряют процесс сходимости к оптимуму, а также всегда позволяют найти эффективное решение [3].

Муравьиный алгоритм

Колония муравьев может рассматриваться как многоагентная система, в которой каждый агент (муравей) функционирует автономно по определенным правилам. В противовес почти примитивному поведению агентов, поведение всей системы получается на удивление разумным [1]. Примером подтверждения оптимальности поведения муравьиных колоний служит тот факт, что сеть их муравейника близка к минимальному остовному дереву графа. В 1990-х гг. появляются так называемые муравьиные алгоритмы (МА) оптимизации (англ. Ant Colony Optimization, ACO), имитирующие поведение муравьиной колонии и применяемые для решения различных классов задач. На сегодняшний день эти методы стали весьма конкурентноспособны по сравнению с другими эвристическими алгоритмами оптимизации [5–6].

Обычно процесс поведения муравьев моделируют на некотором графе. В данной статье рассмотрена его реализация для поиска наименьшего гамильтонова цикла в полном графе, для которого основное правило поведения муравьев можно отобразить следующей формулой:

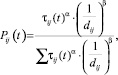(1)

где Pij(t) – вероятность перехода из вершины i в вершину j в текущий момент времени; τij(t) – концентрация феромона (следа, оставляемого муравьями), которая определяет предпочтительность движения по данному пути; dij – его длина, а α и β – некоторые константы, определяющие работу алгоритма, задаваемые пользователем.

На каждой итерации алгоритма изменение концентрации феромона происходит по нижеприведенной формуле

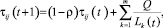(2)

где Q – параметр, имеющий значение порядка обрабатываемых длин; Lk– длина маршрута; p – коэффициент испарения феромона.

Смысл данной формулы заключается в том, что каждый раз, когда муравей проходит по какому-либо отрезку, он оставляет след феромона в размере, обратно пропорциональном длине этого отрезка. Чем большее количество раз муравьи пройдут по некоторому пути, тем выше будет концентрация феромона, тем с большей вероятностью они будут снова выбирать этот путь.

Повысить эффективности работы алгоритма можно путем ведения так называемых «элитных» муравьёв, которые усиливают рёбра лучшего текущего маршрута, найденного с начала работы алгоритма. Тогда если в колонии есть e элитных муравьёв, то рёбра маршрута получат дополнительное количество феромона по нижеприведенной формуле

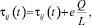(3)

где e – количество элитных муравьев; L – длина наилучшего текущего маршрута.

То есть после каждой итерации увеличивается концентрация феромона на тех ребрах, по которым проложен самый эффективный путь. Таким образом, ускоряется сходимость к оптимуму посредством увеличения концентрации феромона на отдельно взятых ребрах. По результатам проведенных исследований, наиболее оптимальным количеством элитных муравьев является 3, данное число сочетает в себе баланс скорости сходимости и точности получаемых решений. При e = 1 точность наиболее высока, а при увеличении этого значения требуется все меньшее количество итераций для получения локального тупика, когда дальнейшая работа алгоритма не приводит к улучшению результата [1].

Исследование влияния параметров и некоторых модификаций

Подобрать оптимальные значения параметров α и β из формулы (1) возможно экспериментальным путем. Для вышеописанного алгоритма было проведено исследование влияния этих параметров на эффективность полученных решений. Для произвольно сгенерированных 80 вершин графа в табл. 1 отображены полученные значения, лучшие сочетания выделены цветом.

Из таблицы видно, что изменение значений параметров α и β приводит к существенным изменениям полученных решений. Лучшие результаты были получены при следующих значениях параметров: (α = 2, β = 1) и (α = 1, β = 5). Увеличение значения первого параметра (увеличивается зависимость получаемого решения от концентрации феромона) приводит к увеличению разброса решений, в данном случае работа муравьиного алгоритма носит скорее эвристический характер. Увеличение значения второго параметра (увеличивается зависимость получаемого решения от длины) приводит к уменьшению разброса решений, и алгоритм начинает работать, прежде всего, как «точный» метод. Далее проведем исследование работы указанных вариантов алгоритма. Для удобства условно назовем МА с (α = 2, β = 1) эвристическим муравьиным алгоритмом (ЭМА), а МА с (α = 1 и β = 5) точным муравьиным алгоритмом (ТМА).

Таблица 1

Зависимость эффективности решения от выбранных параметров на примере задачи с 80 точками

Для МА были разработаны следующие модификации:

1) «предварительный расчет начальной концентрации феромона (РК)»;

2) «расчет начального пути методом наименьших отрезков (МНО)»;

3) «сглаживание методом ветвей и границ (МВГ)».

Под первой модификацией подразумевается, что начальная концентрация феромона рассчитывается из матрицы расстояний до работы основного цикла. Эта модификация подобна работе большого количества элитных муравьев, когда усиливается скорость сходимости, но падает точность вычислений. Вторая модификация предполагает, что начальное приближение пути рассчитывается по методу наименьших отрезков, который благодаря элитным муравьям станет приоритетным на начальных этапах итераций, то есть также возрастает скорость сходимости в разы, но падает точность. Третья модификация вступает в силу после применения элитных муравьев на каждой итерации, но только во второй половине основного цикла алгоритма, для того чтобы не тратить временные ресурсы на поиск заведомо неэффективных решений. Сглаживание ведется методом ветвей и границ для каждых пяти точек всего пути, то есть данная модификация позволяет избежать угловатостей и ускорить не только процесс сходимости, но и повысить точность найденного решения [1].

Для сравнительного анализа предложенных модификаций на основе полученных ТМА и ЭМА построим таблицу для тех же 80 точек, что и в табл. 1, а также добавим результаты работы для 30 и 150 вершин; количество итераций 1000.

Таким образом, можно сделать выводы, что модификации, такие как РК и МНО, целесообразно использовать для быстрого получения эффективного решения, так как сходимость в данном случае крайне высока и необходимость в большом количестве итераций отпадает, однако вероятность получения оптимального решения для большого количества точек минимальна. Максимальную эффективность данные модификации показали при использовании муравьиного алгоритма с α > β, так как в ТМА и так уже используются точные вычисления благодаря большому значению β (длины отрезков в значительной мере влияют на вероятность перехода муравья из одной вершины в другую) и использование иных традиционных алгоритмов только ухудшает его работу. Модификация методом ветвей и границ всегда улучшает работу любого МА с незначительной потерей скорости работы, поэтому оптимальные решения были получены именно с этой модификацией в ТМА (они выделены в табл. 2). Однако хоть ТМА и всегда находит решение лучше, чем ЭМА с любыми модификациями, но привязка к длине отрезка в большей степени, чем к концентрации феромона, может привести к нахождению локального тупика (когда дальнейшая работа алгоритма не улучшит полученное решение).

Выводы

Для сравнительного анализа эффективности работы эвристических алгоритмов был реализован программный комплекс [4], в котором проводилось исследование различных методов оптимизации, а также анализировались их модификации. Лучшие реализации муравьиного и генетического алгоритмов были объединены в гибридный муравьино-генетический алгоритм (МГА), в котором инициализация начальной популяции происходит путем применения МА, после чего алгоритм начинает работать как ГА. В этом случае генетический алгоритм уже оперирует с результатами МА, совершенствуя общий результат посредством скрещивания.

Таблица 2

Сравнительный анализ модифицированного и не модифицированного МА

В разработанном программном комплексе имеется возможность выбора различных алгоритмов поиска, просмотра затраченного времени на поиск и длины полученного решения, а также настройки основных параметров эвристических алгоритмов. Результаты работы (длины найденных путей) исследуемых алгоритмов для 100–140 точек отражены на рис. 1.

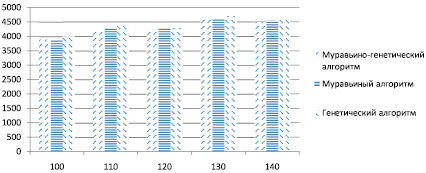
Рис. 1. Сравнительный анализ полученных решений для 100–140 точек

Из рисунка видно, что до 140 точек генетический алгоритм незначительно уступает другим алгоритмам в точности найденного решения. На рис. 2 отражены результаты работы алгоритмов для 300–340 точек. Здесь модифицированный генетический алгоритм значительно уступает гибридному и муравьиному алгоритмам в точности определения длины найденного маршрута, поэтому можно сделать вывод, что его не следует применять в задачах с большим количеством исходных данных – для относительно быстрого поиска решений целесообразно использовать МА или МГА.

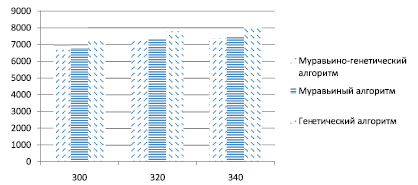
Рис. 2. Сравнительный анализ полученных решений для 300–340 точек

Рецензенты:

Видовский Л.А., д.т.н., доцент, профессор кафедры ИСП, ФГБОУ ВПО «Кубанский государственный технологический университет», г. Краснодар;

Ключко В.И., д.т.н., профессор кафедры ИСП, ФГБОУ ВПО «Кубанский государственный технологический университет», г. Краснодар.

Работа поступила в редакцию 01.08.2013.