Компьютерное моделирование нашло практическое применение во всех сферах хозяйственной деятельности человека. Обзор систем математического моделирования показывает, что аналитическое моделирование (АМ) является едва ли не самым популярным средством моделирования. Основная его ценность состоит в применении методологии системного анализа. АМ разрешает осуществить исследование анализируемой или проектируемой системы по схеме операционного исследования, содержащего ряд взаимосвязанных этапов:
1) содержательная постановка задачи;
2) разработка концептуальной модели;
3) разработка и программная реализация имитационной модели;
4) проверка правильности;
5) проверка достоверности и адекватности математической модели и оценка точности результатов моделирования;
6) планирование и проведение экспериментов;
7) принятие решений.
Все приведенное выше позволяет использовать АМ как универсальный подход для принятия решений в условиях неопределенности с учетом трудно формализуемых факторов в математических моделях, а также применять основные принципы системного подхода для решения практических задач. Широкому внедрению этого метода на практике способствует его универсальность, заключающаяся в быстрой перенастройке моделей при изменении исходных данных математического моделирования, что сокращает сроки системного этапа проектирования. С другой стороны, сложность аналитических зависимостей препятствует применению метода, что и вызывает необходимость создания программных средств для их расчета. Усилия разработчиков программных средств направлены на упрощение программных реализаций моделей: для этих целей созданы методы приближенных вычислений. Основное назначение всех этих средств – уменьшение трудоемкости создания и расчета АМ, а также экспериментирования с математическими моделями.
Целью работы является создание программного комплекса (ПК) для визуального моделирования стохастических сетей массового обслуживания (СеМО) и сбора статистики по элементам математической модели и всей стохастической сети в целом.
Объектом разработки являются математические модели ядра операционных систем (ОС), реализующие различные функции управления процессами и потоками в многопроцессорных и распределенных системах, в частности, функции планирования и диспетчеризации задач.
Постановка задачи
Известно большое число дисциплин планирования и диспетчеризации, которые заключаются в правилах формирования очереди готовых задач и правилах выбора задач на выполнение. В частности, к ним относятся дисциплины FIFO, LIFO, приоритетные дисциплины с абсолютными, относительными и смешанными приоритетами, а также некоторая смесь этих дисциплин, обеспечивающая расширенную область использования операционной системы, например, одновременно и для систем общего назначения, и систем реального времени. При планировании и диспетчеризации процессов (потоков) следует учитывать также ограниченность ресурсов вычислительной системы (ВС), например, ограниченное число буферов для хранения дескрипторов задач, составляющих элементы очереди [11].
При проектировании новых многопроцессорных ОС и, в частности, планировщиков и диспетчеров задач, необходимо определять эффективность возможных реализаций. Одним из главных критериев при таких разработках является производительность. Для оценки показателей производительности диспетчеров задач авторами разработаны аналитические математические модели n-процессорных систем с алгоритмами планирования процессов по стратегии разделения времени (рис. 1, а) и разделения пространства (рис. 1, б) [11]. Модели представлены в виде разомкнутых СеМО.
В математической модели с разделением времени заявка (задача), поступающая извне (источника S0), или после переключения контекста, может быть назначена в любой процессор (ЦП), поэтому представляется в виде многоканальной СМО (S1) (см. рис. 1, а). Свободные ЦП запрашивают диспетчер, функциями которого является выбор задачи из очереди, выбор одного из ЦП для обслуживания задачи и передача ему управления для её обслуживания. Выбор задачи и выбор обслуживающего процессора может осуществляться либо по приоритетному принципу, либо в порядке FIFO, причем очередь имеет ограничение на число мест. Поскольку управление задачами производится одним диспетчером, следовательно, он является общим ресурсом для всех запрашивающих процессоров. Поэтому математической моделью механизма доступа процессоров к диспетчеру является одноканальная СМО (S2). Достоинство такого диспетчера в том, что единственная очередь обеспечивает автоматическую балансировку загрузки ЦП. Следует учитывать, что очередь формирует планировщик задач, поэтому именно планировщик выступает в качестве источника заявок сети (S0).
Принятая на обслуживание задача находится в очереди до тех пор, пока не поступит на выполнение в один из ЦП. Если используется режим квантования, то незавершенная задача по окончании текущего кванта помещается в конец глобальной очереди, иначе результат выдается пользователю, а в очереди освобождается одно место. При завершении выполнения текущей задачи диспетчер просматривает очередь, и если в ней имеются заявки на обслуживание, то назначается на выполнение задача, стоящая в голове списка или наиболее приоритетная. Если очередь пуста, свободные ЦП переходят в режим ожидания. Если очередь заполнена, то вновь поступившая заявка получает отказ (в реальной системе планировщик не выбирает задачу из внешней памяти).
Диспетчер представляет собой программу, которая выполняется на одном из ЦП, причем вызвать эту программу может любой свободный ЦП, запрашивающий очередной процесс (задачу) для обслуживания. Поэтому источником заявок для диспетчера выступают свободные процессоры, запрашивающие очередную задачу для обслуживания. Если диспетчер занят, то запрашивающий ЦП приостанавливается; из них образуется своеобразная очередь O1 [3, 6].
Математическая модель с разделением пространства состоит из n одноканальных СМО (S1, …, Sn) (см. рис. 1, б). Каждая такая СМО моделирует обслуживание в процессорном узле, в состав которого входит ЦП и диспетчер. Источник S0 моделирует потоки заявок l0 (пользовательских процессов, формируемых планировщиком) и поглощает обслуженные заявки (выдача результата пользователю). Вновь поступившая задача помещается в очередь к одному из процессорных узлов, длина которой ограничена. Если имеется свободное место в одной из очередей, то задача занимает его. Принятая на обслуживание задача находится в локальной очереди до тех пор, пока не поступит на выполнение в процессор. Если используется режим квантования, то незавершенная задача по окончании текущего кванта помещается в конец той же очереди, где она находилась ранее, иначе результат выдается пользователю, а в локальной очереди освобождается одно место. При завершении выполнения задачи диспетчер просматривает локальную очередь. Если в ней имеются заявки на обслуживание, то назначается на выполнение задача, стоящая в голове списка (FIFO) или наиболее приоритетная. Если очередь пуста, ЦП переходит в режим ожидания.
Планировщик задач в данном случае не только формирует очереди в процессорных узлах, но и производит балансировку загрузки по некоторому алгоритму. Поэтому заявки могут извлекаться из i-й очереди и передаваться с некоторой вероятностью в очередь наименее загруженного j-го процессорного узла.
а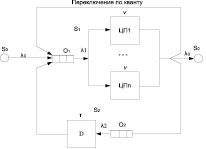 
б 
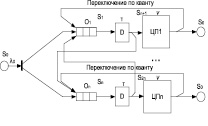
Рис. 1. Схема аналитической модели n-процессорной системы с алгоритмами планирования процессов по стратегии разделения времени (а) и разделения пространства (б)
Если считать, что приложения формируют простейшие потоки запросов, а времена обслуживания подчиняются экспоненциальному закону, то модели процессорных узлов и диспетчера представляются марковскими СМО типа М/М/1/, М/М/n/m, где m – число мест в очереди готовых задач. Если используются приоритетные очереди задач или приоритетный выбор обслуживающего процессора, то в качестве моделей необходимо использовать полумарковские СМО типа М/G/1, М/G/1/m, М/G/n/m, в которых длительность обслуживания заявок распределена по произвольному закону [1, 4, 5].
Рассмотрим подробнее разработку математической модели многопроцессорной системы, использующей диспетчер с разделением времени. В ней СМО 1 представляет модель обслуживания в процессорных узлах, СМО 2 – модель обслуживания диспетчером задач. Пусть очередь в СМО 1 организована по принципу FIFO и имеет ограничение на число мест. Тогда время ожидания в очереди определяется известной формулой Литтла: w1 = l1/λ1, где λ1 – интенсивность потока заявок на входе СМО 1, а l1 – среднее число задач, находящихся в очереди, значение которого может быть определяется формулой [5, 10]:
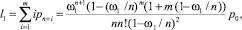(1)
где n – число обслуживающих устройств (процессоров); m – число мест в очереди; ω1 = λ1/μ1 – приведенная интенсивность потока – среднее число задач, поступающих в СМО S1 за время обслуживания одной задачи; μ1 – интенсивность обслуживания пользовательских задач – обратная величина от среднего времени обслуживания одной задачи; p0 – вероятность отсутствия заявок в СМО, определяется по формуле, полученной в [4, 7]:
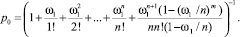(2)
Будем считать, что диспетчер осуществляет выбор обслуживающего процессора по приоритетному принципу. Тогда математическая модель диспетчера будет представлена одноканальной СМО (S2) с приоритетной очередью. Предположим, что обслуживание диспетчером заключается в переключении контекста i-го процессора средним временем τi.
ЦП являются источником запросов к диспетчеру, интенсивность которого составляет λ2. Пусть диспетчер при выборе обслуживающего процессора использует относительные приоритеты, а каждый процессор имеет номер приоритета k, причем чем выше номер, тем ниже приоритет. Время ожидания обслуживания диспетчером потока, формируемого процессором k-го приоритета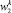 
, определится по формуле [1, 8]
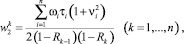(3)
где Rk–1 = ρ1 + ... + ρk–1 и Rk–1 = ρ1 + ... + ρk – загрузки, создаваемые потоками заявок от свободных процессоров ЦП1, ..., ЦПk–1 и ЦП1, ..., ЦПk соответственно; νi = σi/τi – коэффициент вариации времени обслуживания, определяющий отношение среднеквадратичного отклонения σi длительности обслуживания к его математическому ожиданию τi.
Интенсивности λ1 и λ2 будут зависеть от входящей интенсивности задач источника S0 и вероятностей переходов из S1 в S2 (P12) и из S1 в S0 (P10). Поскольку в СМО S2 возникают отказы в обслуживании, то интенсивности потоков λ1 и λ2 будут снижаться:
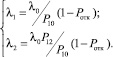(4)
Отказ в обслуживании происходит в том случае, когда все m мест заняты:
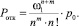(5)
Заявки перемещаются по сети и могут многократно посещать одну и ту же СМО, поэтому вводится коэффициент передач [1, 5], показывающий, сколько раз задача будет проходить через i-ю СМО,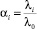 
, где λi – интенсивность на входе i-й СМО, λ0 – интенсивность источника входящего потока заявок.
Поскольку каждая задача может получить обслуживание в i-й СМО в среднем αi раз, то соответственно время ожидания обслуживания и время пребывания ее в системе увеличится в αi раз. Среднее время ожидания задачи в очередях сети
W = α1w1 + α2w2. (6)
Реализация программного комплекса
Для расчета вероятностно-временных характеристик представленных математических моделей была поставлена задача разработки специализированного ПК для визуального аналитического моделирования диспетчеров задач многопроцессорных систем на основе сетей массового обслуживания (СеМО). Для реализации алгоритма математического моделирования использована среда программирования Borland Delphi 7.
В ПК имеется возможность задания вероятностей передач заявок в стохастической сети, могут варьироваться и редактироваться параметры СМО, создается отчет по результатам исследования. В качестве моделей стохастических СМО используются одноканальные и многоканальные СМО с неограниченной очередью и с ограничением очереди, без приоритетов, с относительными приоритетами, с абсолютными приоритетами и со смешанными приоритетами, учитывается коэффициент вариации для моделей M/G/1.
Конфигурация сети задается матрицей вероятностей передач или визуально в виде графа передач [1].
Задачи, которые решаются с помощью ПК:
- ввод, просмотр и редактирование исходных данных;
- расчет характеристик стохастических сетей СМО;
- вариация параметров некоторых СМО и расчет характеристик СМО с учетом варьируемых параметров (каждый параметр в отдельности);
- вывод результатов расчетов на экран, в текстовый файл отчета или в виде графика.
Для реализации выделенных задач разработаны отдельные программные модули.
Для проведения расчетов в программу заносятся следующие параметры:
- Наименование СМО.
- Время обслуживания.
- Ограничение на длину очереди.
- Система с относительным приоритетом.
- Число классов приоритетов.
- Доля входного потока.
- Количество каналов в каждой из СМО.
- Быстродействие каждого канала СМО.
- Матрица вероятностей передач.
- Интенсивность входного потока.
Варьируемые параметры имеют следующие значения:
- Время обслуживания в СМО.
- Интенсивность входного потока.
- Число каналов в СМО.
- Число мест в СМО.
- Начальное значение варьируемого параметра.
- Количество циклов прогонки.
Расчетными характеристиками являются:
а) характеристики отдельных СМО:
- Коэффициент передачи сети.
- Интенсивность входного потока.
- Коэффициент загрузки.
- Среднее число занятых каналов.
- Среднее число заявок в СМО.
- Средняя длина очереди.
- Среднее время ожидания заявки в очереди.
- Среднее время пребывания заявки в очереди.
б) характеристики всей сети в целом:
- среднее количество заявок в сети;
- среднее время пребывания одной заявки в сети;
- среднее время ожидания одной заявки в сети;
- общая длина очередей.
На рис. 2 представлена последовательность действий, выполняемых ПК.
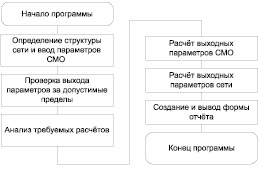
Рис. 2. Последовательность действий, выполняемых ПК
После загрузки программы на исполнение открывается окно для ввода структуры сети. В дальнейшем происходит изменений конфигурации сетевой модели, ввод параметров сети и отдельных СМО оператором и ввод варьируемых параметров сети (при необходимости). При запуске на расчет проверяются введенные параметры на допустимость, если все параметры верны, запускается расчет статистики по заданным параметрам.
Основным является блок, в котором производятся расчеты сетевой модели и отдельных СМО. В основе расчетов лежат теоретический и математический аппараты теории вычислительных систем. В общем случае статистические характеристики сети складываются из характеристик СМО, в нее входящих, а те, в свою очередь, от характеристик, рассчитанных для каждого канала и приоритета внутри данных СМО.
Представим основные окна программного комплекса (см. рис. 4):
– Окно визуального редактора (рис. 4, а), где пользователь может с помощью графических предоставленных элементов создавать и редактировать схему стохастической сети;
– Окно редактора матрицы вероятности передач (рис. 4, б) позволяет редактировать вероятности переходов заявок от одной СМО к другой, а также редактировать интенсивность входного потока заявок;
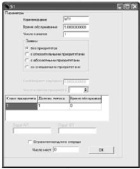
– Окно параметров СМО (рис. 4, в) позволяет редактировать основные характеристики каждой СМО (учитывать приоритет, число мест в очереди, число каналов, время обслуживания);
– Окно параметров расчета сети (рис. 4, г) позволяет выбрать расчет с варьируемыми параметрами и объявить эти параметры.
– Окно результатов (рис. 4, д) представляет собой таблицу отчета по статистическим расчетам, проведенным для данной сети.
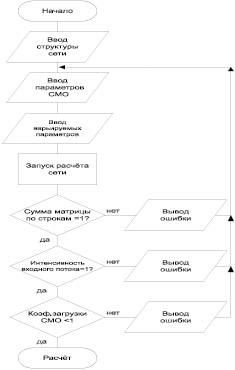
Рис. 3. Схема алгоритма ввода начальных параметров сети и их проверки
При проектировании ПК использовался модульный принцип написания программ, что позволило значительно облегчить разработку ПК и его отладку [2]. В ходе проектирования были достигнуты все поставленные перед разработчиками цели. ПК гарантирует быстроту доступа к информации, удобный пользовательский интерфейс.
ПК зарегистрирован в Федеральной службе по интеллектуальной собственности. Свидетельство о государственной регистрации программ для ЭВМ № 2013611117 зарегистрировано 9 января 2013 г.
Представленный ПК применен для математического моделирования приведенного выше диспетчера задач со стратегией разделения времени, имеющего следующие исходные данные:
– интенсивность входного потока задач λ0 = 0,03; 0,06; 0,09 задач/мкс (соответственно низкая, средняя и высокая загрузка ЦП);
– время переключения контекста диспетчером τ = 9 мкс, что соответствует средним значениям времени переключения контекста ОС «мягкого» реального времени (например, в Linux RT) [9];
– вероятность выхода обслуженной задачи P10 = 0,05. Вероятность отправки задачи на дообслуживание P12 = 0,95;
– время обработки одной задачи ЦП ν = 10 мс. Размер общей очереди перед процессорами N = 128 задач;
– количество ЦП варьировалось от 4 до 100.
Результаты математического моделирования показали, что диспетчер с указанными параметрами имеет латентность (время ожидания обслуживания), не превышающую 13 мкс. Такая латентность соответветсвует многим существующим системам реального времени, например, LinuxRT [9].
а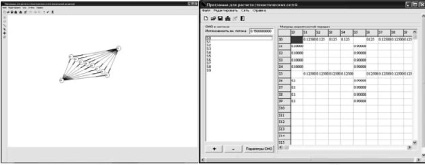 
б
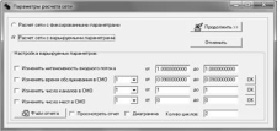г 
г
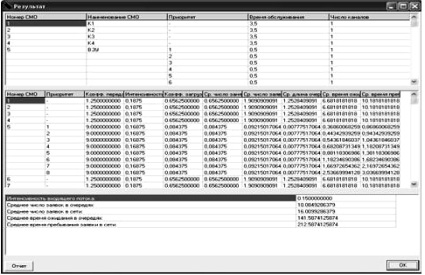
Рис. 4. Основные окна программного комплекса
Адекватность аналитической модели диспетчеров задач с разделением времени подтверждается данными, полученными в ходе имитационного моделирования. Погрешность аналитических моделей не превышает 20 %, что вполне приемлемо для оценки вариантов реализации диспетчеров на системном этапе проектирования.
Выводы
Существенным отличием разработанного ПК является возможность расчета стохастических сетей МО, содержащих СМО с ограниченной длиной очереди, СМО с приоритетами, а также возможность расчета по нескольким одновременно варьируемым исходным параметрам. ПК обеспечивает удобство ввода и отображения исходных данных, а также наглядное представление результатов математического моделирования в виде таблиц или графиков.
Работа выполнена при финансовой поддержке Федеральной целевой программы «Научные и научно-педагогические кадры инновационной России» на 2009–2013 годы (соглашение № 14.B37.21.0597).
Рецензенты:
Бабич М.Ю., д.т.н., главный специалист ОАО «НПП «Рубин», г. Пенза;
Бутаев М.М., д.т.н., ученый секретарь Совета ОАО «НПП «Рубин», г. Пенза.
Работа поступила в редакцию 01.08.2013.