Достижение компетентностного уровня образования предполагает модернизацию образовательных технологий, научную основу которой составляют фундаментальные дидактические теории и методология научной деятельности. В этой связи актуализируется проблема выполнения системного синтеза методологической и дидактической составляющей педагогических знаний, необходимого для создания научно и практически обоснованных инструментов развития компетенций.
Ориентируясь на него в процессе обучения студентов использованию статистических методов в сфере экономики, можно утверждать, что реализация компетентностного подхода не сводится к усилению прикладного компонента содержания образования на основе решения прикладных задач, направленных на овладение умениями применять теоретические знания в конкретных практических ситуациях. Компетенции связаны в целом с формированием научных представлений обучаемых об окружающем мире и обогащением способов взаимодействия с ним. Поэтому целесообразно в каждой теме выделить ключевые задачи, которые предполагают элементы исследования в процессе интеграции теоретической и прикладной составляющих учебных курсов.
Такие комплексные задачи позволяют осуществить проблемный анализ реальных ситуаций, предусматривающий полноценную реализацию принципов научной деятельности. Приведем пример ключевой задачи из курса «Эконометрика».
На четырех предприятиях (В1, В2, В3, В4) проверялись три технологии производства (А1, А2, А3) однотипных изделий. Требуется установить влияние на производительность труда технологий (фактора А) и предприятий (фактора В) [2]. Проверим следующие гипотезы:
О влиянии фактора А
Н0: различия в производительности труда между технологиями являются не более выраженными, чем случайные различия внутри каждой группы.
Н1: различия в производительности труда между технологиями являются более выраженными, чем случайные различия внутри каждой группы.
О влиянии фактора В
Н0: различия в производительности труда между предприятиями являются не более выраженными, чем случайные различия внутри каждой группы.
Н1: различия в производительности труда между предприятиями являются более выраженными, чем случайные различия внутри каждой группы.
О взаимодействии факторов А и В
Н0: влияние технологий на производительность труда одинаково на всех предприятиях и наоборот.
Н1: влияние технологий на производительность труда различно на всех предприятиях и наоборот.
Результаты дисперсионного анализа приведены в следующей табл. 1.
Таблица 1
Результаты дисперсионного анализа
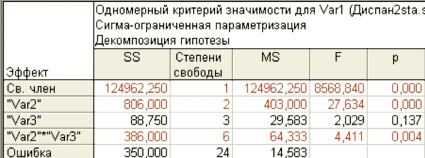
Как видно из табл. 1, установлено влияние фактора «технология» и взаимодействие факторов «технология» и «предприятие» на производительность труда.
Средние значения между всеми градациями фактора «технология» значимо отличаются друг от друга, т.е. все технологии существенно различаются по влиянию на производительность труда (табл. 2).
Таблица 2
Результаты сравнения средних с помощью множественного t-критерия Стьюдента для фактора «технология»
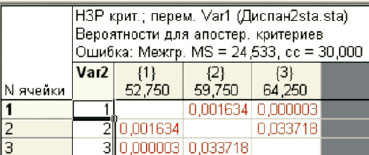
Сравнивая ее среднее значение для каждой градации, видим, что наиболее высокая производительность труда в среднем у первой технологии, затем у второй, самая низкая – у третьей. На графике этот результат очевиден (рис. 1).
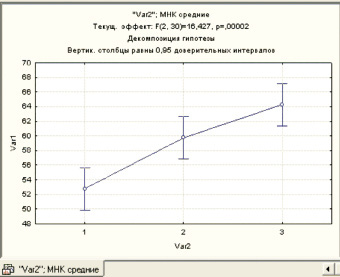
Рис. 1. График средних для фактора «технология»
Аналогичное сравнение средних для экспериментального плана, отражающего взаимодействие факторов (12 групп) выполнить весьма трудно. Поэтому сначала обратимся к графику взаимодействий (рис. 2).
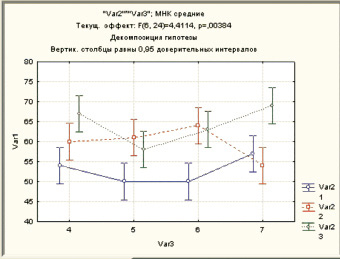
Рис. 2. График взаимодействия факторов «технология» и «предприятие»
Данный график показывает, как соотносится производительность труда по разным технологиям с конкретным предприятием. Для предприятий 4 (1) и 7 (4) наиболее эффективна третья технология, а для предприятий 5 (2) и 6 (3) примерно одинаково эффективны вторая и третья технологии. Наименее эффективна первая технология. Об этом же свидетельствуют результаты апостериорного сравнения средних. Учитывая различия между 24 и 34, можно считать, что для предприятия 4 (1) предпочтительнее технологии 2 и 3, если сравнивать их с первой, и предпочтительнее 3, если сравнивать ее со второй. А у предприятия 7 (4) нет предпочтений относительно первой и второй технологии, зато явно предпочтительнее по сравнению с ними третья технология. Очевидно, для предприятий 5 (2) и 6 (3) менее эффективна третья технология по сравнению со второй и третьей, а вторая и третья практически не отличаются.
Интерпретация результатов дисперсионного анализа выглядит громоздкой, поскольку одновременно учитывается и влияние фактора «технология». На графике это выражено в том, что первая к оси абсцисс линия «почти» не пересекает остальные две, т.е. первая технология гораздо менее эффективна, чем две предыдущие. Причем пересечение последних выражено также неотчетливо.
Эта задача является комплексной по социально-экономическому содержанию, т.к. предполагает исследование влияния разных факторов и их взаимодействия на результативный признак. Ее решение связано с построением различных математических моделей [2, 4, 5], возникающих в ходе применения соответствующего статистического метода и наглядного представления полученных результатов.
Кроме того, можно обозначить направление дальнейшего исследования, связанного с установлением влияния всех существенных факторов на производительность труда [1,3]. В математическом смысле ставится задача исследования влияния взаимодействия факторов второго (трех факторов) порядка и выше на результативный признак. Если в качестве третьего фактора рассматривать, например, квалификацию работников, то можно выдвинуть гипотезу о том, что наибольший эффект взаимодействия факторов «предприятие» и «технология» достигается в том случае, когда квалификация работников высокая. В данном случае, если рассматривать две градации фактора «квалификация», полный экспериментальный план будет включать 24 группы. Даже при установлении влияния взаимодействия трех факторов предсказать заранее наличие или отсутствие различий в средних показателях производительности труда между этими группами невозможно. Необходимо выполнение детального сравнения средних между ними.
Если учитывать структуру данных и результаты дисперсионного анализа, можно расширить возможности их математической обработки первичных данных и качественной интерпретации ее результатов, например, по следующим направлениям:
1. Фактор «квалификация работника» может быть количественным, переведенным в ранговую шкалу. Возможно получение более точного результата при использовании его в качестве независимой переменной в процессе регрессионного анализа. При построении адекватного уравнения коэффициенты регрессии интерпретируются, в частности, в линейной модели, с учетом вклада других неучтенных факторов. Такая интерпретация (и в случае нелинейной регрессии) может служить важным дополнением к результатам дисперсионного анализа. На основе же полученного уравнения можно провести более адекватное ранжирование этого показателя и предусмотреть его целесообразные вариации.
2. При невыполнении математических допущений регрессионного анализа используют непараметрические аналоги (критерии Джонкира, Крускала‒Уоллиса и др.), которые применяются, во-первых, когда исследуется влияние одного фактора. Во-вторых, они позволяют выявить характер влияния фактора лишь частично (интерпретация результата обладает большой неопределенностью). Поэтому можно рассматривать по отношению ко всем выборкам сразу комбинации из трех факторов, интегрировав их в виде одного обобщенного фактора. Тогда полученный результат будет иметь еще большую неопределенность. Возникает противоречивая ситуация: «Не учитывать нормальность распределения признака и применять параметрические методы (в частности, дисперсионный анализ) или использовать непараметрические методы?» Как нам представляется, разумно сочетать в комплексе параметрические и непараметрические методы, имея в виду последствия нарушений математических ограничений. В некоторых случаях (например, когда эмпирическое распределение отличается от нормального) они не приводят к серьезным искажениям полученного результата, но позволяют при этом сделать более конструктивные выводы или хотя бы уточнить гипотезы.
3. Необходимо учитывать все существенные факторы и типичные условия, в которых они могут действовать. Кроме того, может заслуживать отдельного внимания какой-либо специфический фактор (даже латентный), выступающий, например, как катализатор взаимодействия непосредственно наблюдаемых существенных факторов.
Заключение
Таким образом, реализация ключевых задач, имеющих многофункциональный характер и направленных на формирование исследовательских умений и навыков студентов позволяет усовершенствовать процесс изучения статистических методов в следующих аспектах:
1. Представить в содержании учебных дисциплин единство трех компонент: теоретической, прикладной и методологической.
2. Обеспечить приоритетное положение методологической составляющей, рассматриваемой в широком смысле не только в связи овладением конкретной системой научных методов познания, но и в плане формирования представлений о современном исследовательском аппарате и месте математики в познании и исследовании закономерностей развития природы и общества.
3. Усилить мировоззренческий и специально научный смысл предлагаемого студентам учебного материала.
4. Раскрыть суть математической и содержательной интерпретации результатов статистического анализа.
Рецензенты:
Шварц К.Г., д.ф.-м.н., профессор Пермского государственного национального исследовательского университета, г. Пермь;
Дубровский А.В., д.п.н., профессор Пермского института (филиала) РГТЭУ, г. Пермь.
Работа поступила в редакцию 11.07.2013.



