В задачах управления сложными системами так или иначе задействована статистическая информация, которая формирует наблюдения [1–5]. Совокупность наблюдений, в свою очередь, формирует статистическую выборку, по которой строятся разного рода статистические оценки, на основании которых делаются выводы и принимаются решения. При достаточном размере выборочной совокупности, сформированной с помощью простого случайного отбора, в ней будут представлены все категории статистических данных, присутствующие в генеральной совокупности и примерно в тех же самых пропорциях.
На практике реализация вероятностных выборок, сформированных в соответствии со всеми предъявляемыми к ним требованиями, как правило, невозможна. Это касается как простого случайного отбора, так и стратифицированных и многоступенчатых выборок.
В отдельности сами по себе возникающие погрешности не велики, что позволяет предполагать однородность выборки наблюдений. С другой стороны, наложение допущений может в результате давать недопустимые отклонения практической реализации от её теоретического аналога. Действительно, этим недостатком обладают все стохастические процессы выбора наблюдений – в данном случае реализации репрезентативной выборки.
В связи с этим после проведения исследований возникает задача оценки адекватной реализации вероятностной модели при практической её реализации.
Алгоритм оценки точностиполученных результатов
Для оценки точности результатов при исследовании риска предлагаются пошаговый способ (алгоритм) построения оценки, позволяющий получить оценку с заданной точностью или, в крайнем случае, при невозможности получить заданную точность, определить оценку полученной точности [1].
Пусть статистика Т может быть найдена в общем случае как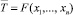 
, например,
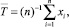
где n – количество наблюдений случайной величины Х.
Зададим некоторое n и получим следующую статистику по первым n наблюдениям (первый шаг):
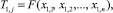
где j = 1 (первый шаг оценки точности), например,
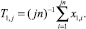
Далее по следующим n наблюдениям получим статистику:
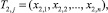
например,
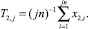
Двойная индексация указывает на то, что для построения статистик T1,j и T2,j одинаковое количество наблюдений, но они не пересекаются. Вычислим статистику T3,j = (T1,j + T2,j)/2.
Далее для построения оценок (второй шаг) добавляется ещё по n наблюдений и т.д. То есть построение оценок становится последовательной процедурой. На первом шаге процедуры берется по n наблюдений для построения статистик T1,j и T2,j, на втором шаге – 2n наблюдений и т.д.
В принятых обозначениях x1,i и x2,i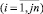 
– наблюдения, по которым строится оценка, j = 1,2,... – число шагов для достижения заданной точности ε (ε ‒ наперед заданное число, например, из серии 0,1; 0,01; 0,001 и так далее). Число шагов j принимает значение j0, при котором впервые выполняется неравенство
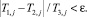
Тогда за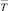 
может быть принята статистика 
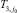, а за выборочную дисперсию 
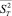статистика 
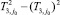, где
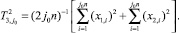
Таким образом,
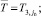(1)
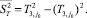(2)
Понятно, что при принятых обозначениях для вычисления с заданной точностью ε необходимо наблюдать N = 2j0n раз случайную величину Х. Если наблюдаемую последовательность случайной величины Х упорядочить в порядке возрастания и обозначить её y1, y2, ..., yN, то выборочная квантиль порядка q равна:
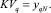. (3)
Формулы (1)–(3) позволяют оценить важнейшие выборочные характеристики по наблюдениям, проведенным в рамках исследований.
Такой алгоритм оценки точности полученных результатов применим при достаточно больших объемах выборки.
В случае, если объемы выборки невелики, то возможно применить скорректированный алгоритм.
Пусть статистика Т может быть найдена в общем случае как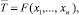 
например,
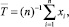
гдеъ n – количество наблюдений случайной величины Х.
Зададим некоторое n и получим следующую статистику по первым n наблюдениям (первый шаг):
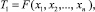
например,
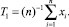
Далее зададим некоторое λ (0 < λ ≤ 1) и построим оценку по первым n(1 + λ) наблюдениям (второй шаг):
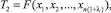
например,
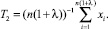
Теперь зададим ε – точность оценки, например, из серии 0,1; 0,01; 0,001 и так далее. Здесь ε = 0,1 соответствует отклонению полученной оценки от истинного значения не более чем на 10 процентов. Проверим неравенство:
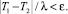
Если неравенство справедливо, то требуемая точность достигнута. В противном случае необходимы дополнительные наблюдения. Их количество на третьем шаге определим как n(1 + λ)2. Очевидно, что при продолжении вышеописанной процедуры построения оценки на j-м шаге количество наблюдений, по которым строится оценка, равно n(1 + λ)j–1.
Заметим, что на каждом последующем шаге можно прибавлять ровно nλ наблюдений. Но этот случай здесь рассматривать не будем, так как с весьма очевидным достоинством – фиксированное число дополнительных наблюдений на каждом шаге, есть вполне очевидные недостатки – длительный процесс достижения заданной точности и изменение формулы неравенства достижения заданной точности на каждом шаге построения оценки.
Нетрудно видеть, что в результате проведения последовательной процедуры получения оценки получится последовательность:
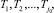
где j0 определяется как минимальное j, при котором выполняется неравенство
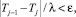
то есть
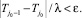
Если заданная точность не может быть получена, то в этом случае целесообразно оценить точность полученной оценки, зафиксировав максимально возможное число шагов процедуры, равное j1. Для этого устанавливается минимальное значение ε0, для которого справедливо неравенство:
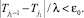
Пример первый
Проводились социологические исследования. По группе респондентов определенной категории из 1000 человек оценивалась вероятность отнесения респондентом своего здоровья к группе «Здоровье очень хорошее или скорее хорошее». В принятых обозначениях n равнялось 200. На первом шаге были получены оценки максимального правдоподобия:
T1,1 = 0,92;
T2,1 = 0,67;
T3,1 = 0,795.
Тогда
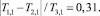
что соответствует тому, что оценка имеет погрешность до 31 %.
На втором шаге были получены следующие оценки:
T1,2 = 0,82;
T2,2 = 0,775;
T3,2 = 0,7975.
Тогда
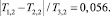
На основании этого равенства можно утверждать, что в группе респондентов определенной категории с вероятностью 0,7975 респондент относит свое здоровье к группе «Здоровье очень хорошее или скорее хорошее» и доля ошибки этой вероятности не превышает 0,056 (или 5,6 %).
Пример второй
Проводились социологические исследования. По группе респондентов определенной категории из 2000 человек оценивалась вероятность отнесения респондентом своего здоровья к группе «Здоровье очень хорошее или скорее хорошее». В принятых обозначениях n равнялось 200. На первом шаге были получены оценки максимального правдоподобия:
T1,1 = 0,8;
T2,1 = 0,6;
T3,1 = 0,7.
Тогда
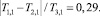
что соответствует тому, что оценка имеет погрешность до 29 %.
На втором шаге были получены следующие оценки:
T1,2 = 0,78;
T2,2 = 0,62;
T3,2 = 0,7.
Тогда
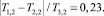
что соответствует тому, что оценка имеет погрешность до 23 %.
И так далее. Пока на пятом шаге не были получены следующие оценки:
T1,5 = 0,72;
T2,5 = 0,69;
T3,5 = 0,705.
Тогда
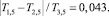
что соответствует тому, что оценка имеет погрешность до 4,3 %.
На основании этого равенства можно утверждать, что в группе респондентов определенной категории с вероятностью 0,705 респондент относит свое здоровье к группе «Здоровье очень хорошее или скорее хорошее» и доля ошибки этой вероятности не превышает 0,042 (или 4,2 %).
Результаты исследования восприятия рисков для здоровья населением региона (приведенного в примере), в частности, выделенные информационные поля восприятия рисков, установленные зоны недостаточной и неадекватной информированности о рисках для здоровья, лежат в основе рекомендаций по совершенствованию информационной политики для управленческих структур федерального и регионального уровней. Это значит, что необходимо иметь возможность распространить результаты выборочного опроса населения региона по теме восприятия рисков здоровью на всю генеральную совокупность. Предложенные способы оценки точности результатов эмпирического социологического исследования позволяют избежать смещений выборки, дают возможность экстраполировать полученные данные на генеральную совокупность максимально обоснованно.
Заключение
В случае, когда исследователь ограничен временными или материальными рамками, может случиться такое, что требуемая точность оценок не будет достигнута. В этом случае целесообразно оценить точность полученных оценок, зафиксировав максимально возможное число шагов процедуры, равное j1. Для этого устанавливается минимальное значение ε0, для которого справедливо неравенство:
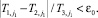
Здесь ε0 – достигнутая точность.
Рецензенты:
Пенский О.Г., д.т.н., доцент, профессор кафедры процессов управления и компьютерной безопасности, Пермский государственный национальный исследовательский университет, г. Пермь;
Ясницкий Л.Н., д.т.н., профессор, заведующий кафедрой прикладной информатики, Пермский государственный гуманитарно-педагогический университет, г. Пермь.
Работа поступила в редакцию 11.07.2013.