Управление сложными объектами, как правило, осуществляется в условиях недостатка и неточности информации, что может привести к принятию ошибочных решений и серьёзным ошибкам в управлении. В такой ситуации наиболее рациональным является применение современных информационных технологий для автоматизированного управления сложными процессами с помощью системы поддержки принятия решений (СППР). СППР необходимо использовать, когда процесс принятия решений ввиду необходимости учета субъективного мнения не может быть полностью формализован и реализован на ЭВМ. Такая система выступает в роли помощника, который позволяет расширить возможности человека, но не заменяет его мнение или систему предпочтений. Таким образом, СППР можно определить как человеко-машинную информационную систему, используемую для поддержки действий в ситуациях, когда невозможно создать автоматическую систему представления и реализации всего процесса оценки и выбора альтернатив.
Большинство СППР работает с числовыми данными, аналитическими моделями и решает проблемы, которые предварительно описываются на языке таких моделей. Однако СППР могут выполнять и некоторые интеллектуальные функции, если в их структуру включить базу знаний и использовать механизм логического вывода. В этом случае СППР становится способной работать в условиях неполноты исходной информации, использовать вероятностные выводы, вырабатывать суждения и объяснения, которые выдаются в качестве рекомендаций при принятии решений, реализуемых на базе СППР.
Одним из наиболее сложных технологических процессов является процесс производства цветных металлов, в частности, меди. Помимо высокого уровня сложности металлургические процессы характеризуются неопределённостью изменения параметров и трудностью получения данных. Существующие в настоящее время логические и математические модели не позволяют корректно управлять таким процессом с помощью АСУ.
Процесс электролитического рафинирования относится к гидрометаллургическим процессам. Существующие в настоящее время СППР используются преимущественно для пирометаллургических процессов, например, в алюминиевой промышленности. В частности, СППР «Стабилизация состава электролита на базе математической модели» [5] рассчитывает для каждого электролизера добавки сырья AlF3 для корректировки криолитового отношения электролита как важнейшего параметра его химического состава.
Что касается автоматизации гидрометаллургических процессов, в [2] была разработана математическая модель процесса электролитического рафинирования меди и структура информационно-управляющей системы, на основе которой создан компьютерный тренажёр. В качестве исходных данных для построения моделей используются экспериментальные зависимости выходных показателей от входных и управляющих воздействий [4]. По полученным массивам экспериментальных данных строились полиномиальные регрессионные уравнения. С помощью компьютерного тренажёра была также исследована проблема повышения технико-экономических показателей процесса электролиза.
Данная работа является продолжением исследования, начатого в [2]. Основной целью данной работы является разработка алгоритма управления процессом электролитического рафинирования меди и построение СППР как основной части информационно управляющей системы на базе математической модели данного процесса.
Математическая модель процесса и постановка задачи управления
Процесс электролитического рафинирования ведут в электролизерах, которые называют ваннами. Ванны изготавливают монолитные из железобетона, собирая их в блоки по 10-20 ванн, а затем в серии, состоящие, как правило, из двух блоков. Учитывая агрессивность электролита, содержащего серную кислоту высокой концентрации, внутреннюю часть ванн футеруют. Внутренние размеры ванны не стандартизованы. Примерные размеры ванн: длина от 3,5 до 5,5 м, ширина от 1 до 1,1 м и глубина 1,2–1,3 м. Размеры электродов на разных заводах различны. С введением механизации разгрузочных работ стали применять аноды больших размеров – 860×860 мм. Масса анодов на некоторых заводах достигает 350 кг, а их количество - в среднем 43 штуки. Толщина анодов равна 35–45 мм.
Входными параметрами данного процесса являются плотность тока (D, А/м2); содержание серной кислоты в электролите (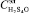 , г/л); содержание сульфата меди в электролите (
, г/л); содержание сульфата меди в электролите (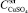 , г/т); содержание меди в электролите (
, г/т); содержание меди в электролите (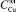 , г/л); скорость подачи электролита (V, л/мин), а выходными – выход по току и производительность.
, г/л); скорость подачи электролита (V, л/мин), а выходными – выход по току и производительность.
Для осуществления управления необходимо иметь специальные инструментальные средства, позволяющие формировать управляющее воздействие. В качестве такого средства предложен виртуальный объект управления – компьютерный тренажер, разработанный на основе математической модели процесса электролитического рафинирования меди [2]:
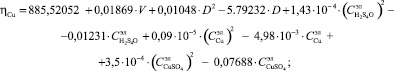 (1)
(1)
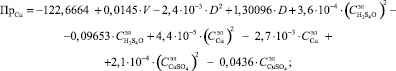 (2)
(2)
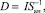 (3)
(3)
где ηCu – оценка математического ожидания выхода по току η, %; ПрCu – оценка математического ожидания производительности электролизёра Пр, тонн/сутки; I – сила тока, кA; Sан – площадь анодов, м2.
Модели построены по данным основной технологической выборки, для которой было произведено 67 измерений на одном лабораторном агрегате за полный технологический цикл. Измерения производились на ЦЭМ-1 и ЦЭМ-3 электролизного цеха НГМК и КУЭМ. Средняя плотность тока по ЦЭМ-1 275 А/м2 и по ЦЭМ-3 310 А/м2. А диапазон изменений выхода по току составлял 84–92 %.
Проверка моделей (1) и (2) показывает, что корреляционное отношение между экспериментальными и расчётными значениями для выхода по току R = 0,989, а для производительности – R = 0,987. Средняя относительная невязка для выхода по току и производительности не превышает 2 %. Оценка общего качества регрессии по критерию Фишера при уровне значимости, равном α = 0,05, и объеме выборки n = 100 показала, что гипотеза о независимости выхода по току и производительности от параметров, указанных в уравнениях (1) и (2), отклоняется. В данном случае для модели выхода по току выборочное значение статистики F = 454,324 больше, чем Fкр = 1,394, аналогично для производительности F = 305,513 > Fкр. Все коэффициенты в моделях (1) и (2) статистически значимы. О законе распределения ошибок можно судить по выборочному значению статистики 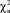 . При уровне значимости α = 0,05 для выхода по току
. При уровне значимости α = 0,05 для выхода по току 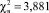 , а для производительности
, а для производительности 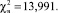 Поскольку критическое значение
Поскольку критическое значение 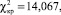 для обоих уравнений выполняется
для обоих уравнений выполняется 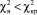 . Следовательно, гипотеза о нормальном законе распределения ошибок модели принимается.
. Следовательно, гипотеза о нормальном законе распределения ошибок модели принимается.
Адекватность построенных моделей подтверждена также проверкой статистической гипотезы о равенстве коэффициентов регрессионных моделей, построенных по основной и контрольной выборкам.
Управление технологическими процессами, как правило, осуществляется по схеме регулирования в режиме настройки. В устройстве управления сравнивается желаемое и действительное значения выходных параметров. Это позволяет определить, насколько состояние объекта отличается от требуемого (задаваемого программой). Управление строится на основе системы функций невязки
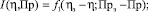 (4)
(4)
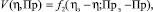 (5)
(5)
с помощью которой рассчитываются управляющие воздействия, а именно сила тока I и скорость циркуляции электролита V в зависимости от отклонения текущего значения каждого из выходных параметров от заданного. Здесь индексом «з» обозначается заданное (предпочтительное) значение контролируемого параметра. Задача управления в этом случае формулируется так: при заданных значениях параметров: 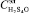 ,
, 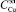 ,
,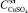 найти значения I и V, удовлетворяющие ограничениям
найти значения I и V, удовлетворяющие ограничениям
24 ≤ I ≤ 25, (6)
12 ≤ V ≤ 30, (7)
при которых ηз – η → min, Прз – Пр → min На практике обычно последние требования заменяются условиями
ηз – η ≤ e1, Прз – Пр ≤ e2, (8)
где e1 и e2 – некоторые достаточно малые величины, e1 ≥ 0, e2 ≥ 0, и задача управления формулируется так: при ограничениях (6)–(7) и заданных значениях 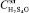 ,
, 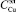 ,
, 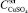 требуется с помощью соответствующих управляющих воздействий I и V добиваться того, чтобы значения целевых функционалов, т.е. выходных параметров h и Пр, в любой момент времени находились в достаточно малой окрестности hз и Прз.
требуется с помощью соответствующих управляющих воздействий I и V добиваться того, чтобы значения целевых функционалов, т.е. выходных параметров h и Пр, в любой момент времени находились в достаточно малой окрестности hз и Прз.
Процесс электролитического рафинирования относится к стохастическим процессам. Кроме того, используемая математическая модель (1)–(3) является статистической. Поэтому при реализации управления процессом электролиза в режиме настройки необходимо учитывать, что условия (8) должны выполняться в смысле математического ожидания:
M[hз – h] ≤ e1, M[Прз – Пр] ≤ e2.
Очевидно, что, имея пусть и оптимальные статистические оценки математических ожиданий, нельзя точно проверить выполнение данных условий. Однако для любого фиксированного набора значений входных и управляющих воздействий можно испытать статистические гипотезы относительно неизвестного условного среднего.
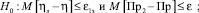
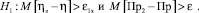
Принятие гипотезы H0 даёт достаточно оснований объявить значения управляющих параметров I и V допустимыми, а принятие гипотезы H1 – недопустимыми.
При любом критерии проверки гипотезы возможны ошибки, когда недопустимые значения I и V объявляются допустимыми, либо допустимые значения объявляются недопустимыми. Устранить указанные ошибки, связанные с неточностью статистической модели, невозможно, однако их можно минимизировать выбором подходящего критерия проверки гипотезы H0.
Поскольку в соответствии с принципом недостаточного обоснования оценки коэффициентов моделей (1)–(2) и соответственно условных средних M[η] и M[Пр] распределены апостериори по нормальному закону, оптимальным для данного закона распределения является критерий максимального правдоподобия [1]. Согласно данному критерию, суммарная вероятность ошибочного решения будет минимальной, если статистические оценки условных математических ожиданий (1) и (2) удовлетворяют неравенствам (8) независимо от значений условных дисперсий. Регулирование значений управляющих воздействий требуется только тогда, когда нарушается хотя бы одно из условий
ηCu ≥ hз – e1, ПрCu ≥ Прз – e2. (9)
Введём обозначения:
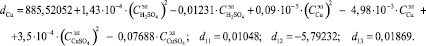
С учетом этих обозначений уравнение (1) примет вид:
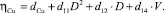 (10)
(10)
Аналогично запишем уравнение (2):
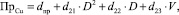 (11)
(11)
где
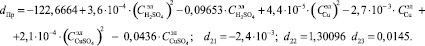
Управляющие воздействия достаточно выбрать такими, при которых неравенства (9) обращаются в равенства, т.е. являются решением системы уравнений
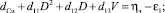
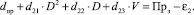
Решая данную систему уравнений, с учётом (3) получаем формулы для расчёта I и V:
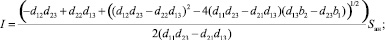 (12)
(12)
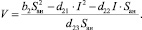 (13)
(13)
Здесь
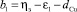 и
и 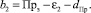
Таким образом, использование соотношений (12)–(13) позволяет выбрать режим, в наибольшей степени отвечающий поставленным требованиям.
Математическая модель принятия решения
Моделирование процессов принятия решения включает в себя формирование исходного множества альтернатив и построение функции выбора. Альтернативами в данном случае являются все возможные состояния S системы, которые определяются наблюдаемыми и управляющими параметрами процесса (рисунок). Эти параметры будем называть атрибутами состояния. Согласно постановке задачи управления выбор наилучшей альтернативы при заданных наблюдаемых параметрах эквивалентен выбору значений управляющих воздействий I и V, при которых выполняются условия (9) для выходных параметров. Поэтому атрибуты I и V являются критериями альтернативы. Таким образом, исходное множество альтернатив Ω состоит из всех возможных пар (I , V) удовлетворяющих ограничениям (6), (7). Каждую пару снова будем обозначать буквой S.
Для построения функции выбора определим на исходном множестве альтернатив Ω булеву функцию f(S), значение которой на альтернативе S равно 1, если предикат 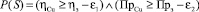 принимает значение «истинно». Если значение P(S) - «ложно», то f(S) = 0. Зададим на исходном множестве альтернатив бинарное отношение Rf по следующему правилу: для любых S1, S2 ∈ Ω выполняется S1 R S2 ⇔ f(S1) > f(S2). Отношение Rf порождает нормальную функцию выбора CR такую, что для любого X ⊆ Ω
принимает значение «истинно». Если значение P(S) - «ложно», то f(S) = 0. Зададим на исходном множестве альтернатив бинарное отношение Rf по следующему правилу: для любых S1, S2 ∈ Ω выполняется S1 R S2 ⇔ f(S1) > f(S2). Отношение Rf порождает нормальную функцию выбора CR такую, что для любого X ⊆ Ω
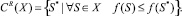 (14)
(14)
Она эквивалентна функции выбора
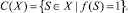 (15)
(15)
В данном случае множество недоминируемых альтернатив состоит из всех пар (I, V) ∈ С(Ω).
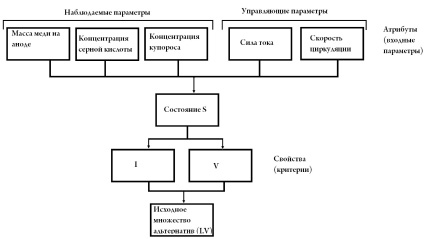
Формирование исходного множества альтернатив
Таким образом, математическая модель управления процессом электролитического рафинирования меди включает в себя модель технологического процесса (1)–(3), технологические ограничения (6), (7), (13) и математическую модель принятия решения, состоящую из исходного множества альтернатив Ω и функции выбора (15). Условие f(S) = 1 обеспечивается формулами для расчёта управляющих воздействий (12), (13).
Алгоритм функционирования СППР
Построенная математическая модель управления технологическим процессом позволяет разработать алгоритм функционирования СППР. Обработка информации в СППР осуществляется как оператором-технологом, так и с помощью математической модели управления технологическим процессом электролитического рафинирования меди. Для разграничения функций модели и человека необходимо составить алгоритм обработки информации в СППР, который будет определять место математической модели и действий оператора в системе управления.
Схема функционирования СППР включает в себя следующие этапы.
- Оператор вводит исходные данные: состав анодного сырья, состав электролита (содержание меди в электролите и анодах, содержание серной кислоты и сульфатов меди в электролите, сила тока и скорость циркуляции электролита).
- Оператор указывает, нужно ли учитывать случайные возмущения. Если нужно, то осуществляется переход к блоку 3, в противном случае – к блоку 4.
- Оператор вводит случайные воздействия.
- Система осуществляет опрос одного из датчиков входных параметров (сила тока, скорость циркуляции электролита, состав анодного сырья и электролита).
- Система проверяет условия управления. Если P(S) = «истинно», то осуществляется переход к блоку 11.
- Система производит расчёт I и V по формулам (12)–(13).
- СППР выводит рекомендации по управлению в случае, когда текущие значения выходных параметров не соответствуют эталонным.
- Оператор вводит рекомендованные значения I и V в систему.
- Система производит расчет прогнозируемого выхода по току и производительности по математическим моделям (1)–(3).
- Система проверяет, соответствуют ли выходные показатели эталонному значению (решается задача принятия решения). В случае «да» осуществляется переход к блоку 11, а в случае «нет» ‒ к блоку 6.
- Система выводит на экран прогнозируемые выходные показатели: выход по току и производительность.
- Система проверяет, произведён ли опрос всех датчиков. Если «нет» осуществляется опрос следующего датчика – переход к блоку 4, если «да» – к блоку 13.
- Система выводит отчёты об итогах работы СППР.
На основе данного алгоритма функционирования разработана СППР, реализующая как режим управления реальным объектом, так и режим компьютерного тренажера (экспертной системы) [3].
Система работает следующим образом. Значения управляющих параметров выбираются, исходя из имеющегося опыта, или рассчитываются по формулам (12) и (13) для идеальных условий функционирования процесса.
Эффективность выбранного значения управляющего воздействия проверяется с помощью компьютерного тренажера путем введения рассчитанного управления. Если реакция СППР по управляющим воздействиям устраивает оператора, то выбранное управление применяется к реальному объекту управления. В противном случае выбор управления необходимо продолжить.
Численный эксперимент проводился при данных, полученных на промышленном электролизёре, где было установлено 43 анода, и их суммарная площадь составляет 30 м2. Показатели сняты при следующих входных и управляющих параметрах: 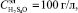 ,
, 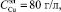 ,
, 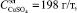 , D = 272 A/м2 и V = 19 л/мин. Средний показатель выхода по току повышается с 87,46, что соответствует среднему выходу тока на реальном агрегате, до 88,99 % и производительности – с 0,0498 до 0,0506 т/сут за один технологический цикл. С учётом границ доверительного интервала для невязки модели выхода по току [0,24, 0,34] с вероятностью 0,95 можно утверждать, что абсолютная погрешность вычисления выхода по току не превышает 0,34 %. Поэтому достигнутый экономический эффект для выхода по току составляет не менее 1,19 % с той же доверительной вероятностью. Аналогично экономический эффект производительности составляет 0,0006 т/сут.
, D = 272 A/м2 и V = 19 л/мин. Средний показатель выхода по току повышается с 87,46, что соответствует среднему выходу тока на реальном агрегате, до 88,99 % и производительности – с 0,0498 до 0,0506 т/сут за один технологический цикл. С учётом границ доверительного интервала для невязки модели выхода по току [0,24, 0,34] с вероятностью 0,95 можно утверждать, что абсолютная погрешность вычисления выхода по току не превышает 0,34 %. Поэтому достигнутый экономический эффект для выхода по току составляет не менее 1,19 % с той же доверительной вероятностью. Аналогично экономический эффект производительности составляет 0,0006 т/сут.
Заключение
В данной статье разработаны математическая модель и алгоритм управления процессом электролитического рафинирования меди. На основе этого алгоритма создана СППР. Использование СППР приводит к стабилизации качества управления, так как уменьшается диапазон колебания выхода по току и производительности, позволяет решить задачу автоматизации процессом электролитического рафинирования и увеличить показатель выхода по току и производительность, т.е. улучшить качество управления электролизом.
Рецензенты:
Ловчиков А.Н., д.т.н., профессор, Сибирский аэрокосмический университет, г. Красноярск;
Ступина А.А., д.т.н., зав. кафедрой информационных технологий менеджмента Института управления бизнес-процессов и экономики Сибирского федерального университета, г. Красноярск.
Работа поступила в редакцию 11.07.2013.



