Разнообразные машины, например, центрифуги и сепараторы для разделения или фильтрования суспензий и эмульсий, газовые и паровые турбинные двигатели, турбокомпрессоры и т.д. имеют в своей конструкции вращающиеся детали различной формы, работающие под воздействием инерционной (центробежной) силы и поверхностных нагрузок. В инженерной практике для расчета механических напряжений, возникающих в самых простых деталях, обечайках, используется безмоментная (мембранная) теория расчета. Эта теория, основанная на гипотезах Г. Кирхгофа (Kirchhoff G.R.), была разработана в 1874 году механиком X. Ароном (Aron H.) и уточнена в 1927 году математиком и механиком А. Лявом (Love A.E.H.)[6]. Однако вследствие гипотез Г. Кирхгофа мембранная теория, разработанная для тонкостенных обечаек, имеет ограничения по соотношению толщины стенки (s) к ее внутреннему радиусу (R) и по величине распределенной поверхностной нагрузки (p). Например, в соответствии с национальным стандартом Российской Федерации (ГОСТ Р 52857-2007) при p ≤ 10 МПа для стали, алюминиевых и медных сплавов при R ≥ 0,1 м условия применения мембранной теории s/R ≤ 0,2. Кроме этого, использование в расчетах обечаек роторов центрифуги сепараторов приближенного значения радиуса кольцевого сечения, не учитывающего толщину стенки ротора (Rt = R + s/2 ≈ R) [4], вносит дополнительную погрешность в определение кольцевых напряжений. При проектировании роторов скоростных центрифуг, у которых фактор разделения (критерий Фруда) Fr > 3500, величина s/R может быть больше 0,2 и погрешность расчета кольцевых напряжений будет еще выше.
Чтобы определить погрешность расчета, возьмем формулу вычисления кольцевого напряжения (σt) в обечайках роторов центрифуг по мембранной теории [4]
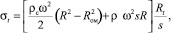
где ρс – плотность обрабатываемой среды; ω – угловая скорость вращения обечайки; R – внутренний радиус обечайки; Rо – средний внутренний радиус обрабатываемой среды или радиус отверстия борта; ρм – плотность материала обечайки; s – толщина обечайки; Rt радиус срединной поверхности кольцевого сечения обечайки. Исходя из данной формулы, относительная погрешность вычисления кольцевого напряжения по общеизвестному методу логарифмического дифференцирования будет определяться выражением:
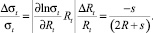
Как следует из полученной формулы, погрешность определения кольцевого напряжения по мембранной теории уже при s/R = 0,2 достигает 9,1 %, что явно недопустимо для расчета опасных в эксплуатации машин.
Для более сложных по форме деталей роторов (дисков, лопаток турбин) используются дифференциальные уравнения равновесия изотропного упругого тела, известные как уравнения равновесия Навье‒Стокса. При их выводе Навье исходил из предположения, что идеально упругое тело состоит из молекул, между которыми при его деформировании возникают силы взаимодействия. Дж. Грин предложил вывод уравнений упругости, опираясь лишь на принцип сохранения энергии. При этом он не вводил каких-либо гипотез относительно молекулярного строения упругих тел. Впервые уравнения равновесия с использованием в них центробежных сил применил Дж.К. Максвелл при решении задачи расчета напряжений во вращающемся тонком диске в докладе «On the equilibrium of elasticsolids» (1850 год). Затем в решении подобных задач уравнения равновесия Навье‒Стокса используются в работах целая плеядой известных ученых [6], однако никто не обращает внимание на парадоксальный характер получаемых зависимостей.
Например, А. Ляв рассматривает вращающийся тонкий диск с концентрическим отверстием при отсутствии внешних нагрузок на его внутренней и наружной цилиндрических поверхностях [3]. Предполагая плоское напряженное состояние, он получает следующие формулы для расчета радиальных (σr) и кольцевых (σt) напряжений:
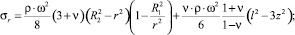
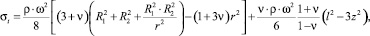
где ρ – плотность материала диска; ω – угловая скорость вращения диска; ν – коэффициент Пуассона; R1, R2 – радиус отверстия и наружный радиус диска; r– текущий радиус рассматриваемого сечения диска; z = ±l – половина толщины диска.
З.Б. Канторович в книге [2] рассматривает вращающийся круглый диск, боковые поверхности которых образованы вращением кривых z = ±f(r) вокруг той же оси (рис. 1). Пренебрегая осевыми перемещениями в диске, он получает дифференциальное уравнение равновесия второго порядка от величины перемещения (u) произвольной точки диска на расстоянии r от оси вращения:
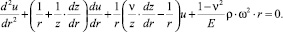
Решение этого дифференциального уравнения для вращающегося плоского диска постоянной толщины при отсутствии внешних нагрузок приводит к следующим формулам:
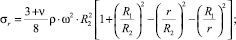
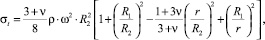
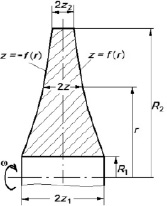
Рис. 1. Параметры диска
где R1, R2 – радиус отверстия и наружный радиус диска.
Еще одно оригинальное решение той же задачи приведено в учебном пособии Ю.Н. Работнова [5]. В нём рассматривается дифференциальное уравнение равновесия элемента диска, которое получено из уравнения равновесия, записанного в форме Лагранжа, после преобразования объемного интеграла в поверхностный интеграл с помощью формулы Гаусса‒Остроградского. В цилиндрических координатах это уравнение имеет вид:
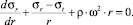
Ю.Н. Работнов вводит некоторую функцию F, которая тождественно удовлетворяет данному уравнению, и для того же случая получает формулы, аналогичные формулам предыдущего примера.
Обращает на себя внимание противоестественный характер зависимостей напряжений от текущего радиуса r, которые получаются как при использовании полученных в работах [1, 2, 4] аналитических формул, так и при численном решении дифференциального уравнения равновесия. Например, на рис. 2 представлены расчетные зависимости, характерные для деталей роторов центрифуг, когда внутренняя цилиндрическая поверхность диска или обечайки нагружена давлением (p1 ≠ 0), а наружная – не имеет нагрузки (p2 = 0). Тот же результат дает расчет диска в современной программе «Autodesk Simulation Multiphysics 2013».
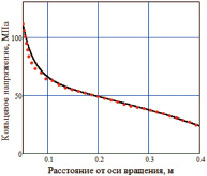
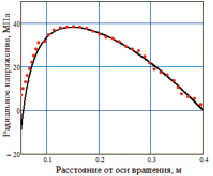
Рис. 2. Характер зависимостей кольцевых и радиальных напряжений от значений текущего радиуса во вращающемся плоском диске с отверстием при R1 = 0,05 м; R2 = 0,4 м; p1 = 10 МПа; p2 = 0; ω = 315 с–1; μ = 0,3; ρ = 7800 кг/м3; Е = 2∙105 МПа (сплошными линиями – по аналитическим зависимостям, точками по программе «Autodesk Simulation Multiphysics»
Во-первых, следует отметить, что уменьшение кольцевого напряжения с ростом текущего радиуса r при квадратичной зависимости от него центробежной силы, вносящей основной вклад в это напряжение, противоречит математической логике. Во-вторых, невозможно дать физическое толкование выраженной экстремальной зависимости радиального напряжения, когда после достижения некоторого значения радиуса r оно начинает уменьшаться.
С.П. Тимошенко в книге «Курс теории упругости» [7] отмечает, что можно подобрать сколько угодно различных распределений напряжений, удовлетворяющих дифференциальным уравнениям равновесия, если не учитывать характер зависимостей между напряжениями и деформациями, возникающими в упругом теле при действии внешних и внутренних сил. Возможно, это и является причиной парадоксального характера зависимостей радиальных и кольцевых напряжений, изображенных на рис. 2. Например, вызывает сомнение то, что при решении дифференциального уравнения равновесия не различается характер изменения радиального напряжения от действия внешних поверхностных и внутренних объемных инерционных сил. Если предположить, что объемные инерционные силы не вызывают изменения радиального напряжения на противоположных гранях элемента тела, а приращение радиальных напряжений происходит только за счет поверхностных сил, то, рассматривая эти нагрузки отдельно в соответствии с принципом независимости действия сил, получим следующие формулы для вычисления суммарных кольцевых и суммарных радиальных напряжений плоского диска постоянной толщины:
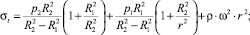 (1)
(1)
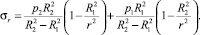 (2)
(2)
a 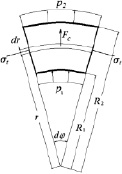 б
б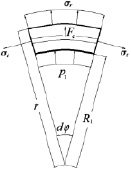
Рис. 3. К выводу формул кольцевых и радиальных напряжений во вращающемся диске с отверстием
Более корректные формулы без введения каких-либо гипотез можно получить следующим оригинальным способом. Рассмотрим равновесие элемента плоского диска, выделенного двумя плоскостями, проходящими через ось вращения под углом dφ друг к другу (рис. 3, a). Сумма проекций сил на линию, делящую пополам угол dφ, после сокращения на dφ будет иметь вид
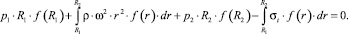 (3)
(3)
Подставляя в уравнение (3) произведения pi∙Ri в виде определенных интегралов 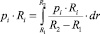 и освобождаясь от интегралов, используя их простейшие свойства, получим формулу для вычисления кольцевого напряжения
и освобождаясь от интегралов, используя их простейшие свойства, получим формулу для вычисления кольцевого напряжения
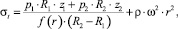 (4)
(4)
где 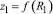 и
и 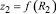 толщины дисков на расстояниях R1 и R2 от оси вращения.
толщины дисков на расстояниях R1 и R2 от оси вращения.
Составим таким же образом уравнение равновесия элемента диска, изображенного на рис. 3, б:
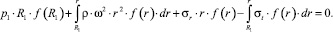 (5)
(5)
После его решения совместно с уравнением (4) получим
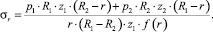 (6)
(6)
Для плоских дисков, по которым можно более точно рассчитывать и вращающиеся цилиндрические обечайки, 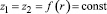 . Тогда из формул (4), (6) формулы кольцевых (σt) и радиальных (σr) напряжений будут иметь вид:
. Тогда из формул (4), (6) формулы кольцевых (σt) и радиальных (σr) напряжений будут иметь вид:
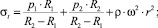 (7)
(7)
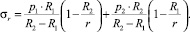 (8)
(8)
a 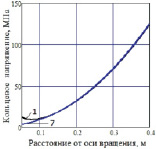 б
б 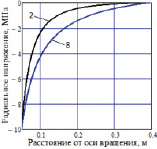
Рис. 4. Уточненный характер зависимостей кольцевых и радиальных напряжений во вращающемся плоском диске с отверстием при тех же, что и на рис. 1, параметрах: a – по формулам (6), (12); б – по формулам (7), (13)
Сравним графически результаты, получаемые по формулам (1), (2) и (7), (8) при тех же, что и на рис 2, параметрах. Как видно из представленных на рис. 4, а и 4, б графиков, кольцевые напряжения, вычисленные по формулам (1), (7), и радиальные напряжения, вычисленные по формулам (2), (8), незначительно отличаются друг от друга. Но существенно отличаются от графиков, изображенных на рис. 2, вычисляемых по известным в теории упругости формулам.
Формулы для других, известных в литературе профилей дисков, решение которых весьма трудоемко [2], легко получить, подставляя в формулы (4), (6) уравнения линий z = f(r), проходящих через две заданные точки (R1, z1) и (R2, z2).
Так, например, для конических дисков, получаем
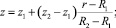 (9)
(9)
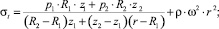 (10)
(10)
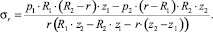 (11)
(11)
Для гиперболических дисков
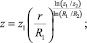 (12)
(12)
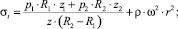 (13)
(13)
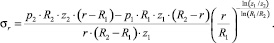 (14)
(14)
Для показательных дисков
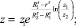 (15)
(15)
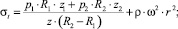 (16)
(16)
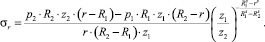 (17)
(17)
где s – константа профиля диска (З.Б. Канторович в [2] рассматривает два близких друг другу профиля: s = 4/3 и s = 2/3).
При анализе решения, полученного для гиперболического диска, З.Б. Канторович [2] отмечает, что исходное дифференциальное уравнение равновесия диска является приближенным, т.к. «…основывается на ряде допущений:
1) длина диска вдоль оси невелика по сравнению с его внешним радиусом;
2) можно пренебречь деформациями диска вдоль оси, которые в действительности имеют место, и т.д.
Результаты расчета тем более точны, чем более плавно изменяется толщина диска». К этому следует отнести и использование при выводе дифференциального уравнения равновесия диска упрощенной линейной связи между напряжениями и деформациями по обобщенному закону Гука, которая также вносит погрешность в расчеты. В использованном здесь методе вывода интегральных уравнений равновесия изотропного упругого тела (3), (5) какие-либо допущения отсутствуют, поэтому полученные формулы (7)‒(17) будут давать более точные значения нормальных напряжений.
Таким образом, новый подход В.М. Беляева к определению радиальных и кольцевых напряженийво вращающихся деталях, во-первых, исправляет парадоксальный характер решения дифференциального уравнения равновесия в теории упругости, существующий уже более 150 лет;
во-вторых, позволяет внести коррективы в инженерные методы прочностного расчета таких опасных деталей, как турбины газовых и паровых двигателей, роторов центрифуг и сепараторов и т.д.;
в третьих, дает основание к изменению подхода в решении дифференциальных уравнений Навье‒Стокса при наличии внутренних сил, которые при преобразовании с помощью формулы Гаусса‒Остроградского изменяют свою точку приложения итем самым вносят ошибку в результат последующего интегрирования уравнений для конкретных случаев.
Рецензенты:
Бальчугов А.В., д.т.н., профессор, проректор по научной работе, ФГБОУ ВПО «Ангарская государственная техническая академия» Министерства образования и науки РФ, г. Ангарск;
Сваровский А.Я., д.т.н., профессор кафедры «Машины и аппараты химических и атомных производств», Северский технологический институт, г. Северск.
Работа поступила в редакцию 01.07.2013.



