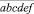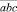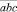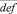Анализ содержания заданий ЕГЭ последних лет, олимпиад школьников, а также подготовительных материалов к ним показывает важность усиления теоретико-числовой подготовки школьников (соответственно, студентов педагогических вузов).
Тематика встречающихся задач: десятичная запись числа; бесконечные десятичные дроби; диофантовы уравнения; свойства делимости; признаки делимости; количество, сумма, произведение натуральных делителей числа; целая часть числа; простые числа.
Кроме того, в последние десятилетия теория чисел находит все больше приложений в теории кодирования, шифровании (например, код РША), т.е. в компьютерной математике.
Целью исследования является выявление форм и методов активизации учебной деятельности студентов в процессе изучения теории чисел.
Решение теоретико-числовых задач использует небольшой по объему математический аппарат, часто требует продолжительных логических рассуждений, применения эвристических методов (перебор вариантов; упрощение формулировки задачи для поиска методов решения; вывод неизвестных учащемуся математических формул (например, произведение всех делителей числа)).
Формулировки задач просты, часто их поймет шестиклассник, решения же их, как правило, очень сложны (достаточно вспомнить «Великую теорему Ферма»).
Решение указанных задач развивает высокую математическую культуру, логику, воспитывает трудолюбие, умение четко и быстро формализовать поставленную нестандартную задачу и предложить несколько направлений ее решения.
Для эффективного обучения школьников, способных справиться с решением олимпиадных задач и задач типа С6 теоретико-числовой направленности, необходимо обратить пристальное внимание на профессиональную подготовку студентов-педагогов направления 050100.62 «Математика».
С этой целью предлагается:
1. Параллельно с изучением курса теории чисел организовать подготовку студентами рефератов по темам:
а) обзор теоретико-числовых задач ЕГЭ (по годам);
б) обзор теоретико-числовых задач математических олимпиад (по уровням, классам, годам);
в) обзор теоретико-числовых задач Турнира Городов;
г) обзор теоретико-числовых задач математического фестиваля «Золотое руно» (по годам и классам);
д) обзор теоретико-числовых задач всероссийской олимпиады школьников имени Л. Эйлера (по годам);
е) поиск простых чисел;
ж) Санкт-Петербургский городской математический центр для одаренных школьников (Рукшин С.Е.);
з) Кировский центр дополнительного образования для детей «Одаренный школьник» (Рубанов И.С.).
2. Предложить написание курсовых работ по темам:
а) системы счисления;
б) простые числа;
в) китайская теорема об остатках;
г) суммы степеней натуральных чисел;
д) диофантовы уравнения второго и высшего порядков;
е) неравенства, системы неравенств с целыми числами;
ж) задачи с параметрами и целые числа;
з) экстремальные задачи с целыми числами;
и) применение теории чисел в шифровании.
3. Организовать спецкурсы и спецсеминары для бакалавров:
а) диофантовы уравнения;
б) теоретико-числовые основы задач ЕГЭ;
в) методы решения олимпиадных задач по теории чисел и др.
4. Привлекать студентов к работе со школьниками в качестве помощников руководителей математических кружков в вузе и школе по подбору задач, проведению отдельных занятий, к проверке работ различных математических соревнований (школьных, районных олимпиад, Турнира Городов и т.п.).
5. Воспитывать критическое отношение к предлагаемым решениям задач. Организовать работу студентов по поиску собственных оригинальных решений (отличных от предлагаемых решений) задач.
Пример 1. Ученик должен был перемножить два трехзначных числа и разделить их произведение на пятизначное. Однако он не заметил знака умножения и принял два записанных рядом трехзначных числа за одно, шестизначное. Поэтому полученное частное (натуральное) оказалось в три раза больше истинного. Найдите все три числа.
Рассмотрим решение, доступное шестикласснику. Обозначим через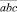 
и 
и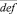скомые трехзначные числа. Из условия задачи:
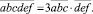
Из этого равенства следует, что число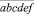 
делится на число 
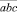, а полученное частное делится на 3. Делим столбиком:
|
|
|
|
|
|
|
|
|
|
|
0
Число 
делится на 3, следовательно, сумма цифр этого числа делится на 3. Поэтому x является одной из цифр: 2, 5 или 8. Если x = 2, то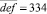 
, 
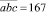. При других значениях x получаем противоречие с условием задачи. Для нахождения пятизначного числа нужно найти все пятизначные делители произведения 167⋅334 = 55778. Такими числами будут 55778, 27889 (55778 не делится на числа 3, 4, 5).
Ответ: (167; 334; 55778), (167; 334; 27889).
6. Подвигнуть будущих педагогов к формированию электронных баз известных сборников задач, созданию собственных банков олимпиадных задач, композиции задач (для начала – по аналогии).
Остановимся подробнее на составлении задач.
Пример 2. Рассмотрим задачу 1.8 из [3]: Докажите, что дробь
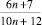
несократима при натуральных n.
Решение. Предположим, что дробь сократима и d – общий делитель числителя и знаменателя. Тогда найдутся целые числа k и t такие, что
.
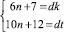Исключим n из системы, умножив равенства на –5 и 3 соответственно и сложив полученные результаты:
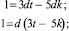
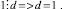
Таким образом, дробь несократима.
Решение предыдущей задачи основано на линейном представлении наибольшего общего делителя взаимно простых чисел 7 и 12. Чтобы получить похожую задачу, рассмотрим дробь
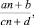
где b и d взаимнопросты.
Найдутся целые u и v такие, что bu + dv = 1. Остается подобрать a и c так, чтобы au + cv = 0 или au = –cv. Например, взяв b = 8, d = 11, получим линейное представление
–4b + 3d = –32 + 33 = 1,
откуда следует u = –4, v = 3. Подберем a и c так чтобы –4a = –3c. Положим a = 9, c = 12.
Получаем задачу: докажите, что дробь
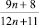
несократима при натуральных n.
Пример 3. ([3]). Решите в натуральных числах уравнение
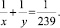
Решение. Из заданного уравнения имеем
xy = 239x + 239y.
Далее,
xy – 239x – 239y + 2392 – 2392 = 0;
x(y – 239) – 239(y – 239) – 2392 = 0;
(y – 239)(x – 239) = 2392.
Число 239 – простое. Полученное уравнение равносильно совокупности систем
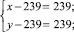
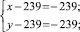
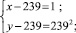
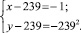
и симметричных последним двум. Решения второй и четвертой систем не удовлетворяют условию задачи. Решениями первой и третьей систем являются (478; 478) и (240; 240⋅239), решение системы, симметричной третьей – (240⋅239; 240). Других решений нет.
Из решения задачи видим, что, заменив число 239 любым простым числом, получим другую, совершенно аналогичную задачу. Если в примере 2 число 239 заменить составным числом (для начала – произведением двух простых чисел), то получим задачу, решаемую таким же методом, но требующую большего количества переборов. Количество переборов в процессе решения задачи можно сократить, вводя дополнительные ограничения в условие задачи (например, требуя x < y).
Пример 4. ([4]). Решите в натуральных числах уравнение
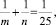
где m > n.
Решение. Из заданного уравнения имеем
mn = 25m + 25n.
mn – 25m – 25n + 252 – 252 = 0;
m(n – 25) – 25(n – 25) – 252 = 0;
(m – 25)(n – 25) = 252.
Полученное уравнение равносильно совокупности систем
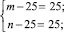
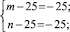
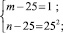
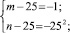
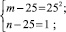
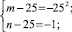
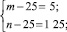
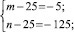
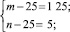
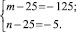
Решениями систем в натуральных числах являются (50; 50), (26; 650), (650; 26), (30; 150), (150; 30). Других решений нет. Условиям задачи удовлетворяют (650; 26),(150; 30).
Количество переборов в процессе решения задачи можно сократить, вводя дополнительные ограничения в условие задачи (например, требуя x<y).
Рецензенты:
Капустина Т.В., д.п.н., к.ф.-м.н., профессор кафедры математического анализа, алгебры и геометрии Елабужского института (филиала) Казанского (Приволжского) федерального университета, г. Елабуга;
Шаймарданов Р.Х., д.п.н., профессор, главный научный сотрудник, ГОУ ВПО ХМАО–Югры «Сургутский государственный педагогический университет», г. Сургут.
Работа поступила в редакцию 21.06.2013