На основе оценки рынка образовательных услуг нами предлагается проанализировать выпуск специалистов вузами Курской области. При разработке модели регулирования выпуска специалистов с высшим профессиональным образованием использованы следующие факторы, выбранные нами на основе имеющейся статистической отчетности по Курской области:
– численность населения региона, тыс.чел. – X1,
– численность экономически активного населения региона, тыс.чел. – Х2;
– среднегодовая численность специалистов, занятых в экономике, тыс.чел. – X3;
– численность специалистов, занятых в экономике, с высшим профессиональным образованием, тыс.чел. – Х4;
– количество зарегистрированных безработных, тыс.чел. – Х5;
– количество зарегистрированных безработных с высшим профессиональным образованием, тыс.чел. – Х6;
– заявленная организациями потребность в работниках, тыс.чел. – Х7;
– численность студентов высших учебных заведений на 10 000 чел. населения – Х8;
– количество вузов в регионе (государственных и негосударственных) – Х9;
– прием в высшие учебные заведения региона, чел. – Х10;
– число предприятий и организаций региона – Х11.
За результирующий показатель (Y) принимается количество выпускников с высшим профессиональным образованием [3, c. 11].
Количественные значения социально-экономических показателей, принимаемых за факторы влияния (Х1, Х2, ..., Х11) и результирующий показатель количества выпускников с высшим профессиональным образованием (Y) за 2005–2011 гг. представлены в табл. 1.
Построенная модель линейной множественной регрессии, рассчитанная с помощью функций табличного процессора MSExcel, имеет вид:
Y = 126278,2 – 60,867∙X1 – 148,195∙X2 – 5,7988∙X3+ 51,507∙X8 + 0,423∙X10 + 0,948∙X11.
Таблица 1
Количественные значения факторов влияния на результирующий показатель выпуска специалистов с ВПО
|
Год |
Факторы |
|||||||||||
|
X1 |
Х2 |
X3 |
Х4 |
Х5 |
Х6 |
Х7 |
Х8 |
Х9 |
Х10 |
Х11 |
Y |
|
|
2005 |
1195,8 |
609,2 |
566,2 |
148,1 |
9,2 |
1,7 |
3,8 |
360 |
13 |
13497 |
25737 |
8584 |
|
2006 |
1177,6 |
592,5 |
549,3 |
146,3 |
8,2 |
1,6 |
4,4 |
372 |
14 |
12117 |
24371 |
11004 |
|
2007 |
1161,6 |
599,7 |
570,3 |
148,8 |
7,5 |
0,9 |
5,5 |
384 |
14 |
14146 |
23923 |
11840 |
|
2008 |
1151,9 |
599,3 |
561,2 |
147,6 |
7,8 |
1,4 |
4,7 |
399 |
14 |
13731 |
22136 |
11445 |
|
2009 |
1143,3 |
588,1 |
536,5 |
141,6 |
11,0 |
2,1 |
2,0 |
419 |
12 |
13404 |
22763 |
15258 |
|
2010 |
1135,0 |
589,0 |
540,6 |
146,0 |
10,0 |
1,9 |
2,8 |
407 |
11 |
15611 |
23128 |
16267 |
|
2011 |
1125,6 |
582,2 |
544,5 |
145,4 |
8,3 |
1,5 |
3,0 |
406 |
10 |
10260 |
23087 |
15472 |
Проведённая оценка коэффициента детерминации R2, стандартной ошибки регрессии, статистической значимости уравнения регрессии (по F-критерию Фишера) и статистической значимости коэффициентов регрессии на основе t-критерия Стьюдента показала, что модель не является адекватной, значимой и не все её параметры соответствуют критерию значимости t-статистики [5, с. 37].
Чтобы разработать качественную модель, необходимо исключить переменные, не удовлетворяющие требованиям значимости [1, с. 115].
Для проведения углубленного корреляционно-регрессионного анализа в первую очередь необходимо построить матрицу коэффициентов парной корреляции для оценки степени влияния факторов на зависимую переменную и друг на друга. Результаты корреляционного анализа, которые показывают взаимосвязь социально-экономических показателей, представлены в табл. 2.
Таблица 2
Корреляционная матрица Пирсона
|
Y |
X1 |
Х2 |
X3 |
Х4 |
Х5 |
Х6 |
Х7 |
Х8 |
Х9 |
Х10 |
Х11 |
|
|
Y |
1 |
|||||||||||
|
X1 |
–0,93 |
1 |
||||||||||
|
Х2 |
–0,89 |
0,84 |
1 |
|||||||||
|
X3 |
–0,81 |
0,63 |
0,85 |
1 |
||||||||
|
Х4 |
–0,65 |
0,49 |
0,68 |
0,88 |
1 |
|||||||
|
Х5 |
0,47 |
–0,21 |
–0,27 |
–0,69 |
–0,77 |
1 |
||||||
|
Х6 |
0,38 |
–0,15 |
–0,32 |
–0,77 |
–0,76 |
0,91 |
1 |
|||||
|
Х7 |
–0,67 |
0,48 |
0,58 |
0,86 |
0,85 |
–0,88 |
–0,89 |
1 |
||||
|
Х8 |
0,89 |
–0,92 |
–0,75 |
–0,71 |
–0,70 |
0,45 |
0,36 |
–0,61 |
1 |
|||
|
Х9 |
–0,77 |
0,71 |
0,70 |
0,68 |
0,51 |
–0,47 |
–0,47 |
0,78 |
–0,58 |
1 |
||
|
Х10 |
0,01 |
0,11 |
0,39 |
0,15 |
0,19 |
0,29 |
0,10 |
0,08 |
0,04 |
0,26 |
1 |
|
|
Х11 |
–0,67 |
0,83 |
0,60 |
0,45 |
0,43 |
–0,08 |
–0,08 |
0,24 |
–0,88 |
0,25 |
–0,04 |
1 |
Одним из условий регрессионной модели является предположение о функциональной независимости объясняющих переменных. Связь между факторами называется мультиколлинеарностью, которая делает вычисление параметров модели либо невозможным, либо затрудняет содержательную интерпретацию параметров модели. Считают явление мультиколлинеарности в исходных данных установленным, если коэффициент парной корреляции между двумя переменными больше 0,8. Чтобы избавиться от мультиколлинеарности, в модель включают лишь один из функционально связанных между собой факторов, причем тот, который в большей степени связан с зависимой переменной [2, с. 23].
В нашем исследовании, анализируя коэффициенты корреляции рассматриваемых факторов, необходимо исключить факторы X4, Х6, Х11 (численность специалистов, занятых в экономике, с высшим профессиональным образованием; количество зарегистрированных безработных с высшим профессиональным образованием; число предприятий и организаций региона) из-за наличия мультиколлинеарности, в результате остаются только не зависимые между собой факторы.
На следующем этапе проведен анализ множественной корреляции для определения уровня значимости модели. В процессе проведения анализа исключаются коэффициенты, уровень значимости которых превышает 0,05. Так, последовательно были исключены такие факторы как X1 – численность населения региона; X7 – заявленная организациями потребность в работниках.
Дальнейший анализ модели проводится с учетом оставшихся факторов.
Построим линейную модель, где Y – количество выпускников с высшим профессиональным образованием; Х1…n – факторы, оказывающие воздействие на количество выпускников с высшим образованием, необходимое региональной экономике. Параметры модели были рассчитаны с помощью функции «Регрессия» табличного процессора MSExcel.
Проведя регрессионный анализ, получим следующие данные:
Y = 132324 – 313,76∙X2 + 91,22∙X3 + 411,273∙X5 + 27,863∙X8 – 439,65∙X9 + 0,5584∙X10
Параметры модели имеют следующую интерпретацию. Коэффициент при Х2, равный 313,76, означает, что при увеличении только фактора X2 (численность экономически активного населения региона) на единицу результативный показатель Y (количество выпускников с ВПО) уменьшается на 313,76; то, что коэффициент при Х3 равен 91,22, означает, что увеличение только фактора Х3 (среднегодовая численность специалистов, занятых в экономике) на 1 приводит в среднем к увеличению Y на 91,22. Коэффициенты при Х5, Х8 и Х10 показывают, что с ростом каждого отдельного фактора на единицу результирующий показатель возрастает соответственно на величину данного коэффициента. При возрастании фактора X9 на единицу Y уменьшится на 439,65.
Оценим значимость полученной модели.
R2 – коэффициент детерминации равен 0,999, он достаточно близок к единице, что свидетельствует об адекватности полученной модели реальным условиям.
Расчетное значение F-критерия:
Fрасч. = 96,7463;
Fтабл. (0,05; 6; 5) = 4,95.
Таким образом, так как Fрасч > Fтабл, то гипотеза о статистической незначимости уравнения регрессии отвергается. Уравнение статистически значимо.
Стандартная ошибка регрессии, объясняющая меру разброса зависимой переменной вокруг линии регрессии, равна 0,001, т.е. оказывает незначительно влияние на регрессионную модель.
Оценим статистическую значимость коэффициентов регрессии на основе t-критерия Стьюдента (табл. 3).
Таблица 3
Расчёт t-критерия Стьюдента
|
Параметр |
Y-пересечение |
Х2 |
Х3 |
Х5 |
Х8 |
Х9 |
Х10 |
|
Коэффициент |
132324 |
–313,76 |
91,22 |
411,273 |
27,863 |
–439,65 |
0,5584 |
|
Стандартная ошибка |
0,01357 |
0,05431 |
0,00962 |
0,01442 |
0,00059 |
0,00872 |
0,01948 |
|
t-статистика |
9753515 |
–5777,17 |
9482,33 |
28521 |
47225,4 |
–50419 |
28,665 |
Подводя итог, следует отметить, что построенная модель регулирования выпуска специалистов с высшим профессиональным образованием адекватна реальным условиям, коэффициенты модели являются статистически значимыми, и предложенную модель можно использовать на практике.
Полученная в результате анализа зависимость позволяет сделать прогноз числа выпускаемых специалистов с высшим образованием.
Использование рассчитанного уравнения множественной регрессии:
Y = 132324 – 313,76∙X2 + 91,22∙X3 + 411,273∙X5 + 27,863∙X8 – 439,65∙X9 + 0,5584∙X10
делает возможным прогнозирование количества выпускников вузов, которые будут трудоустроены в среднесрочной перспективе (2012–2016 гг.) на основе сложившейся тенденции социально-экономических показателей, определенных как значимые факторы влияния.
В ходе исследования развития рынка образовательных услуг Курской области нами спрогнозировано количество выпускников с высшим профессиональным образованием, которые должны быть трудоустроены в среднесрочной перспективе на основе сложившейся тенденции факторов влияния [4, c. 27].
Прогноз количества выпускников с ВПО и влияющих на данный показатель факторов на период 2012–2016 гг. осуществляли по множественной линейной регрессии. Прогнозирование факторов данной модели осуществили с помощью средств Microsoft Excel путем построения уравнение временного тренда.
На рисунке можно проследить изменение результирующего показателя нашей модели – количества выпускников с высшим профессиональным образованием – в прогнозируемом периоде с 2012 по 2016 гг.
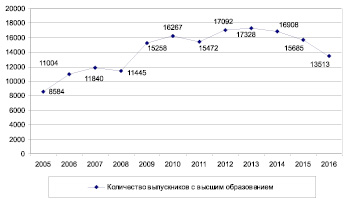
Прогнозные значения числа выпускников с высшим профессиональным образованием на 2012–2016 гг.
Как видно на графике, численность будущих специалистов сначала возрастает в прогнозном периоде, а затем начинает снижаться, что напрямую связано с изменением предложения на рынке труда. Для трудоустройства роста числа работников с ВПО необходимо стимулировать предприятия региона и самих выпускников на взаимное сотрудничество.
Рецензенты:
Левченко В.А., д.э.н., профессор кафедры менеджмента Курского филиала Финансового университета при Правительстве РФ, г. Курск;
Колмыкова Т.С., д.э.н., профессор кафедры финансов и кредита, ФГБОУ ВПО «Юго-Западный государственный университет», г. Курск.
Работа поступила в редакцию 21.06.2013.



