Грунт – это минерально-дисперсное тело, обладающее определенной пористостью. Изменения пористости под влиянием внешних нагрузок от сооружения подчиняются следующим закономерностям: во-первых, изменению коэффициента пористости от давления, сдвигу при трении и скольжения; ламинарной фильтрации; во-вторых, линейной или нелинейной деформируемости. Здесь при оценке сжимаемости грунтов важно выяснить зависимость между изменениями внешней нагрузки и изменением коэффициента пористости грунтов. Если неоднородная грунтовая среда в общем случае обладает свойством нелинейной ползучести, то зависимость между коэффициентом пористости и суммой главных напряжений имеет вид
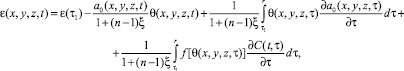(1)
где 
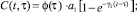(2)
ε(t), θ(t) – эти функции также изменяются по координатам x, y, z; f[θ(τ)] – функция, характеризующая нелинейную зависимость между коэффициентом пористости ε(t) и суммой главных напряжений θ(t) в скелете грунта; φ(τ) – функция старения; a1, γ1 – параметры ползучести; τ1t1 – момент приложения внешней нагрузки; x – коэффициент бокового давления; а0 – коэффициент сжимаемости грунта, который в общем виде может зависеть от глубины исследуемой точки и времени; п – размерность рассматриваемой задачи; C(t, τ) – мера ползучести. Причем здесь функция f[θ(τ)] может изменяться в виде
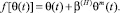(3)
Зависимость (1) при n = 1 и (2), т.е. для одномерной задачи уплотнения однородных грунтов впервые была применена В.А. Флориным [6]. Он теорию упругоползучего тела Г.Н. Маслова‒Н.Х. Арутюняна [1] смог применить к описанию процесса уплотнения глинистых грунтов, обладающих свойством ползучести. Экспериментальные исследования С.Р. Месчяна [5] доказали применимость этой теории к водонасыщенным глинистым грунтам.
Для линейной задачи теории механики уплотняемых пористых упругоползучих неоднородных грунтов зависимость (1) переходит к следующему виду
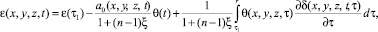(4)
где функции f[θ(t)] и δ(t, τ), входящие соответственно в состав формул (3) и (4), находятся из зависимостей
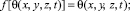
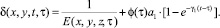(5)
Здесь Е(x, y, z, t) – модуль деформации неоднородного уплотняемого грунта. Функция старения φ(τ) в (5) обычно представляется в виде [1].
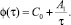(6)
Здесь С0, А1 – опытные данные; τ – время приложения нагрузки.
Эти зависимости, т.е. (1)–(6) будут описывать состояние скелета слабых глинистых грунтов, находящихся под давлением тех или иных внешних нагрузок. Для неоднородного упругого грунта зависимость (4) имеет вид
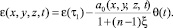(7)
Выражение (7) для одномерной задачи теории консолидации однородного изотропного грунта имеет вид [7]
ε0 – ε = a0σ, (8)
где величины ε0, a0 находятся путем эксперимента или вычислением; a0 – коэффициент сжимаемости; e0 и e – коэффициенты пористости для начального и конечного моментов времени. Причем, проф. Цытович Н.А. считал, что этот закон в механике грунтов имеет такое же большое значение, как и закон Гука в теории сопротивления материалов и коэффициент сжимаемости, а0 является очень важной характеристикой при расчете осадки сооружения.
Между коэффициентом сжимаемости а0 и модулем общей деформации Е существует зависимость [7]
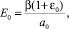(9)
где b – коэффициент, равный для глин 0,43; для суглинков – 0,57; для супесей – 0,72; для песчаных грунтов – 0,76. Зная значение для а0, всегда из (9) можно определить Е0.
Основные разрешающие уравнения механики уплотняемых неоднородных упругоползучих грунтов определим следующим образом. Для этого возьмем уравнение уплотнения для пространственной задачи механики уплотняемых неоднородных грунтов без учета его ползучести, обладающих различными свойствами в вертикальном и горизонтальном направлениях
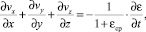(10)
где
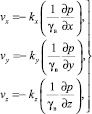(11)
откуда
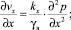
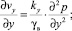(12)
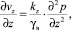
где kx, ky, kz – соответственно коэффициенты фильтрации грунта в вертикальном и горизонтальном направлениях; εср– средний коэффициент пористости в процессе уплотнения; vx, vy, vz – скорости при фильтрации воды к дрену.
Имея в виду (11), (12) уравнение (10) приводим к виду
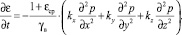(13)
Если в место ε(t) примем (1), то
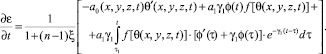
Подставив в (13) последнее соотношение, находим
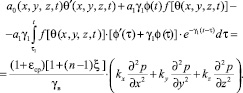(14)
Дифференцируя последнее уравнение (14) по t, затем сложив полученное равенство с (14), предварительно умножив его на g1, получим следующее нелинейное уравнение второго порядка относительно θ(t)
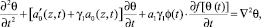(15)
где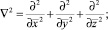 
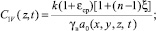(16)
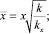
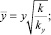
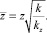(17)
Для одномерной задачи теории консолидации глинистых грунтов
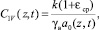(18)
для двумерной задачи
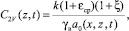(19)
для трехмерной задачи
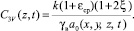(20)
Следовательно, для нахождения искомой функции θ(t), кроме граничных условий, должны быть заданы еще два начальных условий. Одно из них определяется из (14) при t = τ1 = 0, т.е.
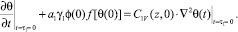(21)
Второе начальное условие вытекает непосредственно из характера приложения нагрузки, т.е.
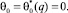(22)
Если вместо нелинейной функции f[θ(t)] примем (3), то нелинейное уравнение (15) имеет вид
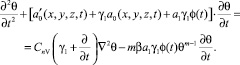(23)
Таким образом, решение нелинейной задачи механики уплотняемых неоднородных глинистых грунтов сводится к решению нелинейного уравнения (23) при (21), (22) начальных и граничных условиях, соответствующих рассматриваемой задаче.
Рассмотрим некоторые частные случаи уравнения (23).
1. Пусть состояние скелета слабых водонасыщенных глинистых грунтов подчиняется линейной наследственной теории Г.Н. Маслова–Н.Х. Арутюняна [1], т.е. уравнению (4). Тогда уравнение (23) приводится к виду
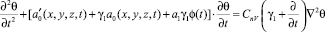(24)
Начальные условия для уравнения (24) будут
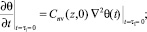(25)
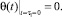(26)
2. Если состояние скелета глинистых грунтов подчиняется закону (7), то уплотняющая среда является упругой и уравнение (23) приводится к виду
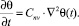(27)
Начальное условие уравнения (27) имеет вид
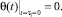(28)
Следует заметить, что все основные уравнения механики уплотняемых водонасыщенных глинистых грунтов приведены относительно суммы главных напряжений θ(t). Можно эти уравнения представить относительно порового давления p(t). Для этого используем условие равновесия вида
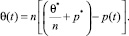(29)
Использовав выражение (29), уравнение (23) относительно порового давления приводим к виду
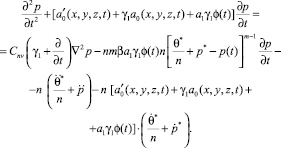(30)
Если состояние скелета водонасыщенного уплотняемого грунта подчиняется закону (4), т.е. где учитывается его линейное свойство ползучести, то основное разрешающее уравнение механики уплотняемых глинистых грунтов имеет вид
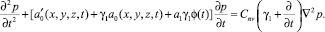(31)
Начальными условиями для (31) будут
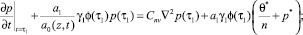(32)
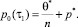(33)
Для упругой задачи уравнение (31) имеет вид
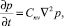(34)
где θ*, p* – сумма главных напряжений и давление в поровой жидкости, соответствующие состоянию мгновенного уплотнения грунта.
Следует заметить, что при решении некоторых задач механики уплотняемых глинистых грунтов, связанных с расчетами вертикальных дрен, песчаными и известковыми сваями уместно использовать указанные выше уравнения (30), (34) соответственно при (32), (26) в цилиндрических координатах.
Эти координаты с декартовыми ортогональными координатами связаны следующими зависимостями
x = rcos φ, y = rsin φ, z = z. (35)
Учитывая (35) основные уравнения механики уплотняемых анизотропных по водопроницаемости глинистых грунтов (30), (31), (34), соответственно можно записать в цилиндрических координатах. При этом выражение для ∇2p имеет вид
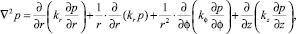(36)
или вместо (36)
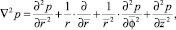(37)
где
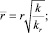
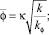
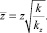
Если иметь в виду, что распределение порового давления не зависит от угла 
, то вместо (37) будем иметь
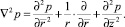(38)
Тогда уравнение (31) при (38) имеет вид
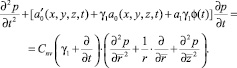(39)
Таким образом, решив уравнения (30), (31), (34), (39) при соответствующих краевых условиях находим решение той или иной задачи теории консолидации земляных масс.
В качестве иллюстрации решим уравнение (31) применительно к одномерной задаче теории уплотнения неоднородных упругоползучих грунтов. Здесь неоднородность грунта изменяется по глубине согласно закону:
E = Emzm, (40)
где Em – модуль деформации на глубине z = 1; m – показатель неоднородности основания, который связан с коэффициентом Пуассона μ0 так μ0(2 + m) = 1. Здесь следует заметить, что Г.К. Клейном [4] разработана методика расчета балок, лежащих на грунтовом основании, модуль деформации которого изменяется по закону (40). Учитывая выражения (9) и (40) для коэффициента сжимаемости, получим
а0 = аz – m;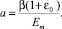 
(41)
При одномерном уплотнении элементарный кубик, выделенный из массива грунта, деформируется в условиях отсутствия бокового расширения. Причем направление сжимаемости кубика-образца совпадает с направлением действия наибольшего главного напряжения. В двух других направлениях деформации равны нулю. В этих условиях относительная деформация уплотнения равна относительной объемной деформации грунта.
Для выяснения общего характера протекания процесса уплотнения достаточно будет рассмотреть отдельные решения именно этой задачи, физическая сторона которой не очень отличается от аналогичных решений трехмерных задач. С другой стороны, исследования одномерного уплотнения более доступны, чем двух- и трехмерных. Кроме того, это дает возможность при рассмотрении процесса уплотнения учесть некоторые факторы, сильно влияющие на него, в частности, можно указать на одновременный учет неоднородности, старения и ползучести уплотняемых грунтов. В связи с этим ниже исследуем процесс уплотнения, происходящий в слое двухфазного грунта.
Рассмотрим случай уплотнения слоя сжимаемого наследственно-стареющего грунта толщиной h, расположенного между фильтрующими слоями (например, песчаными). Пусть он в момент времени t = τ1 подвержен действию внешней распределенной нагрузки с интенсивностью q = q(z, t). Верхняя и нижняя поверхности уплотняемого массива водопроницаемы.
Основное уравнение одномерной задачи механики однородных уплотняемых наследственно-стареющих трехфазных грунтов находим из (30), приняв n = 1, θ* + P* = q(z, t). Если модуль деформации уплотняемого грунта изменяется по глубине, подчиняясь закону (40), а коэффициент сжимаемости по выражению (41), то основное уравнение уплотнения (31) имеет следующий вид:
При этом это уравнение в безразмерных координатах имеет вид:
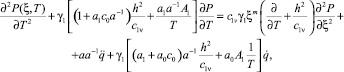(42)
где 
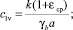
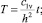
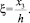(43)
Начальными условиями для данной задачи, согласно (32) и (33), будут:
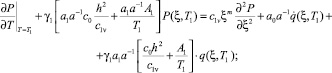(44)
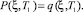(45)
Граничными условиями исследуемой задачи будут:
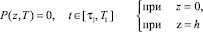
или относительно безразмерных координат
P(ξ, T) = 0 при x = 0
и x = 1 T ∈ [τ1, T1], (46)
Следовательно, задача сводится к решению уравнения (42) при начальных (44), (45) и граничных (46) условиях. Подобная задача также исследована в работах [5, 6] Это решение применительно к данной задаче можно представить так:
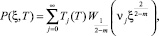
T ∈ [T1, T], ξ ∈ [0, 1], m ≠ 2. (47)
Здесь функция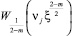 
для целого индекса 
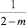, m ≠ 2 имеет вид:
(48)
Она для дробного индекса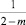 
m ≠ 2 представлена следующим образом:
(49)
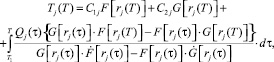(50)
где
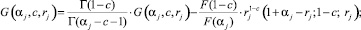
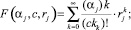
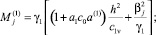
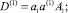
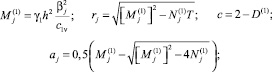
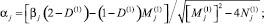
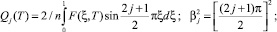
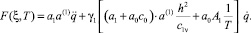
Параметры находятся как решение следующих трансцендентных уравнений для целого индекса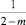 
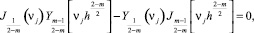(51)
для дробного индекса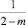 
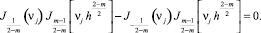(52)
Уравнение (51) и (52) для конкретного числа m имеют бесчисленные множества корней
.
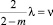Учитывая (48)–(52) расчетную формулу для вычисления распределения порового давления в уплотняемом массиве мощностью h с водопроницаемыми верхней и нижней поверхностями в безразмерных координатах представим следующим образом.
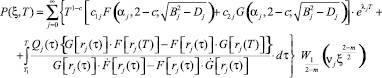(53)
где
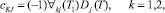
где
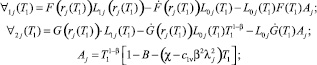
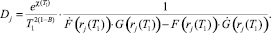
Напряжение в скелете грунта находится из следующего соотношения
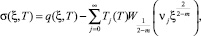(54)
где Tj(T) находится из (50) или (51).
Для вычисления осадок S(T) грунта в безразмерной координате используем формулу вида
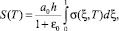(55)
где σ(ξ, T) – напряжение в скелете грунта. Причем при Т → 0 имеем, что σ(ξ, T) → 0, а при Т → ∞ напряжение стремится к q. Следовательно, если поровое давление изменится от q до 0, то напряжение принимает значение от 0 до q. При этом S(T) изменится от 0 до
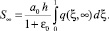(56)
Если q(ξ, T) = q = const то из (48) находим, что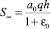 
, т.е. неустановившаяся осадка слоя уплотняемого грунта во времени изменяется в диапазонах от 0 до 
.
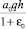Таким образом, процесс возникновения и возрастания порового давления является сложным процессом, зависящим не только от величины, приложенной внешней нагрузкой, но и от времени, плотности и водонасыщенности грунта. Причем, чем плотнее грунт и вязок, тем больше период времени, необходимый для достижения его стационарного напряженного состояния.
Устойчивость самого сооружения в этот период будет в основном зависеть от распределения приложенных нагрузок между скелетом и поровой жидкостью. В этом плане, чем раньше большую нагрузку будет воспринимать на себя скелет, тем устойчивее грунт. Следовательно, сам процесс перераспределения напряжений между скелетом и поровой жидкостью во времени имеет большое практическое значение. При этом одновременный учет старения и ползучести скелета грунта снижает величину порового давления в процессе консолидации. Увеличивает величину начальной осадки и замедляет скорость протекания осадки по сравнению с фильтрационной теорией уплотнения земляных масс. При этом продолжительность протекания осадки по сравнению с фильтрационной теорией сокращается.
Следует заметить, что решению подобных вопросов также посвящены работы [2, 3, 8].
Рецензенты:
Арапов Б., д.т.н., профессор, Южно-казахстанский государственный университет имени М. Ауэзова, г. Шымкент;
Бровко И., д.т.н., профессор, Южно-казахстанский государственный университет имени М. Ауэзова, г. Шымкент.
Работа поступила в редакцию 01.07.2013.