Центробежные крыльчатки (рабочие колеса) относятся к деталям роторной группы. Являясь одним из основных рабочих органов турбонасосных агрегатов и компрессоров, они предназначены для передачи механической энергии потоку газа, протекающему через них. Передача энергии от центробежной крыльчатки к газу происходит благодаря динамическому взаимодействию ее лопастей с протекающей жидкостью (газом). К этим деталям, работающим в условиях больших оборотов (до 30000 об/мин), интенсивного силового, температурного и химического воздействия, предъявляются высокие требования к качеству поверхностного слоя: шероховатости, остаточным напряжениям. Одним из методов достижения заданных технологических параметров поверхностного слоя является применение виброабразивной обработки и виброударного упрочнения [2]. При виброударной обработке интенсивно вибрирующая инструментальная среда, представляющая собой ансамбль частиц, в течение 30–45 минут соударяется с деталью. При соударениях образуется множество локальных отпечатков на поверхности детали, которые формируют упрочненный слой. В отличие от работы [4], где было проведено численное исследование виброабразивной обработки в двухмерной постановке, в настоящей статье приводятся результаты трехмерного математического моделирования процесса виброударного упрочнения крыльчатки.
Центробежная крыльчатка компрессора полуоткрытого типа (рис. 1) предназначена для нагнетания воздуха в цилиндры двигателя внутреннего сгорания. Она содержит 14 лопаток и 14 проточных каналов. Изготавливается крыльчатка объемной горячей многопозиционной штамповкой из алюминиевого сплава АЛ6 с калибровкой. Исходная шероховатость поверхностей лопаток и проточных каналов составляет 23–28 мкм, требуемая конечная шероховатость Rz ≤ 10–15 мкм. Диаметр крыльчатки равен 160 мм, а высота ее – 35 мм.
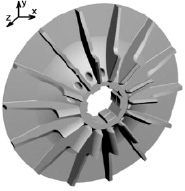
Рис. 1. Исследуемая центробежная крыльчатка компрессора полуоткрытого типа
Для моделирования применяется гетерогенная вычислительная система на базе программно-аппаратной платформы CUDA фирмы NVidia. Основные вычисления производились на специальном сопроцессоре – 3D-видеокарте, а центральный процессор выполнял утилитарные функции (копирование данных в (из) память видеокарты, сохранение информации в базу данных и др.). Данный сопроцессор имеет SIMD-архитектуру, т.е. один поток команд исполняется применительно к множественному потоку данных [1]. Это обеспечивает параллельность вычислений, что в итоге ведет к повышению производительности отдельных алгоритмов, в числе которых алгоритм метода дискретных элементов. Он используется в настоящей работе для моделирования динамики конечного множества частиц инструментальной среды.
В настоящей работе используется модель деформируемых частиц. Такие частицы в точке контакта внедряются друг в друга на малую величину, соизмеримую с высотой их микронеровностей, с определенной силой взаимодействия, которая зависит от величины внедрения. Частицы при контакте взаимодействуют посредством вязкоупругой силы – линейной комбинации закона Гука и вязкой составляющей, характеризующей диссипацию энергии при соударении. Величина нормальной составляющей контактной силы
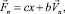 (1)
(1)
где c – коэффициент квазижесткости; b– коэффициент демпфирования.
Коэффициент квазиупругой жесткости характеризует силу отталкивания, а коэффициент демпфирования – потери энергии при соударении. Эти коэффициенты могут быть получены из эксперимента или аналитически, из теории Герца. Уравнение тангенциальной составляющей силы, учитывающей трение Кулона, имеет вид
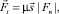 (2)
(2)
где μ – коэффициент вязкого трения, s – единичный вектор, направленный в сторону, противоположную вектору тангенциальной составляющей относительной скорости соударения.
Общая сила взаимодействия будет равна векторной сумме тангенциальной и нормальной составляющих. Модель адекватно описывает поведение трехмерной среды и достаточна проста в реализации.
Трехмерное моделирование динамики процесса виброударного упрочнения было проведено для инструментальной среды, состоящей из 22000 стальных шариков диаметром dш = 5 мм, массой m = 0,000511 кг. Трехмерная модель контейнера и детали представлена конечным множеством элементарных треугольных площадок – сплайнов. Количество сплайнов в моделях контейнера и центробежной крыльчатки компрессора соответственно равно 480 и 49929. На детали большее количество сплайнов выбрано для более точной детализации параметров соударений. Трехмерная модель была разработана в системе трехмерного моделирования 3D Studio Max 2010. При этом сплайновая сетка на детали была дополнительно «нормализована», т.е. ей была придана однородность размеров сплайнов при помощи модификатора «Subdivide» программы 3D Studio Max (см. рис. 2). Детализация модели детали была повышена с 35768 до 49929 сплайнов, а средняя площадь сплайна составила 12,5 мм2 Повышение детализации модели приводит к увеличению точности расчета распределения любого динамического или технологического параметра по трехмерной поверхности.
Контактная модель, используемая для расчета соударений между гранулами, используется и при расчете соударения гранулы о сплайн поверхности детали и контейнера. Отличие состоит в том, что сплайн детали или контейнера в данном случае подменяется фиктивной гранулой значительно большего размера и массы, у которой центр расположен таким образом, что сплайн лежит на ее поверхности [3].
Первой стадией моделирования является задание начальных координат положения всех гранул в свободном трехмерном пространстве контейнера и задание начальных скоростей перемещений. Задание начальной скорости – задача тривиальная, расчет начальных положений гранул в пространстве – задача более затратная с точки зрения объема вычислений. Алгоритм заполнения основан на методе трассировки лучей, когда из тестируемой точки пространства «испускается» луч и подсчитывается количество пересечений со сплайнами модели. Если количество пересечений нечетное, значит, точка находится внутри объема, ограниченного трехмерной моделью. Видно, что для размещения всех частиц в пространстве необходимо выполнить n×k тестов «луч-сплайн» на предмет пересечений, где n – количество частиц, а k – количество сплайнов. Тест одной точки можно делать независимо от теста другой, при этом алгоритм хорошо распараллеливается.
а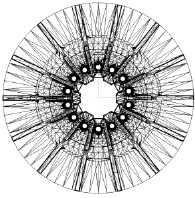 б
б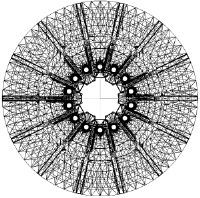
Рис. 2. Генерация сетки треугольных сплайнов (проекция модели на плоскость X0Y):а – начальная неоптимизированная структура сплайнов; б – структура сплайнов, обработанная модификатором «subdivide»
В «классическом» алгоритме, когда программный код выполняется на центральном процессоре, имеется функция Reset(), которая в цикле последовательно вызывается для каждой тестируемой точки. Для реализации параллельной обработки точек трехмерного пространства указанная функция была переопределена со спецификатором __global__ следующим образом: __global__ void Reset_D(...).
Этот спецификатор указывает, что запускается функция хостом (host), т.е. центральным процессором, а исполняется на устройстве (device), т.е. графическом процессоре [5]. Перед самим вызовом функции ядра указывается конфигурация вычислительной сетки (grid), так как весь массив запускаемых параллельных потоков имеет свою структуру и подразделяется на блоки [1]. Указывается количество блоков в сетке и количество потоков в блоке. Задается конфигурация специальными символами < < < > > > , между которыми и определяется конкретная конфигурация сетки [1]:
Reset_D < < < numBlocks, numThreads > > > (...)
Количество нитей на блок и количество блоков по каждому измерению сетки имеет ограничение. Чтобы узнать максимальные значения количества нитей в блоке и количество блоков, необходимо обратиться к драйверу устройства посредством вызова функции cuda Get Device Properties [5].
Программно-аппаратная конфигурация компьютера: ЦП Intel Core i7 950 3.06 GHz HT, ОЗУ 3×4 GB DDR3 1333 MHz Kingston, накопитель SSD: OCZ Vertex 3 60 GB SATA3, ОС Microsoft Windows 7 Pro x64, MS SQL Server 2008 Standard Edition, видеокарта Asus GeForce GTX580 DirectCU2 в качестве вычислительного сопроцессора.
Время моделирования за счет применения указанной ранее программно-аппаратной конфигурации компьютера и параллельных вычислений сокращается до 1500 раз по сравнению с вычислениями на центральном процессоре.
Быстродействие вычислений при выполнении алгоритма начального заполнения контейнера на графическом процессоре (ГП) 3D-видеокарты в сотни и более раз больше, чем на центральном процессоре (ЦП) (рис. 3).
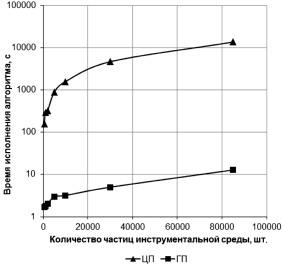
Рис. 3. Производительность алгоритма «заполнения» контейнера при выполнении трехмерного моделирования на центральном процессоре (ЦП) и графической плате (ГП)
Производительность моделирования трехмерной задачи примерно равна времени двухмерного моделирования (рис. 4). В результате трехмерного моделирования по разработанной программе получена информация о трехмерном координатном распределении скоростных и энергетических параметров, технологических параметров формирования поверхностного слоя для конечного множества сплайнов детали сложной формы, с учетом ее размеров, формы и расположения поверхности, физико-механических свойств ее материала, размерных и физико-механических параметров инструментальной среды.
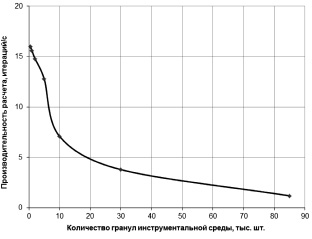
Рис. 4. Зависимость производительности трехмерного моделирования от количества частиц вибрирующей инструментальной среды
Рецензенты:
Копылов Ю.Р., д.т.н., профессор Воронежского государственного технического университета, г. Воронеж;
Колодежнов В.Н., д.т.н., профессор Воронежского государственного университета инженерных технологий, г. Воронеж.
Работа поступила в редакцию 01.07.2013.



